Взаимодействие токов. 2 страница

Рис. 84.

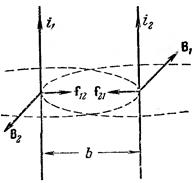Рис. 85.

Следовательно, согласно (46.2) на единицу длины тока i ₁ действует сила

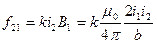(46.3)

Для силы f ₁₂, действующей на единицу длины тока i₂ получается аналогичное выражение С помощью правила левой руки легко установить, что при одинаковом направлении токов они притягивают друг друга, а при различном – отталкивают.

Выражение (46.3) совпадает с формулой (38.2 ), если положить k = 1. Следовательно, в СИ закон Ампера имеет вид

d f = i d l ´ B (46.4)

Соответственно

d f = iВ d l sin a. (46.5)

Сила Лоренца. Ее действие на движущиеся заряды.

Проводник, по которому течет ток, отличается от проводника без тока лишь тем, что в нем происходит упорядоченное движение носителей заряда. Отсюда напрашивается вывод, что сила, действующая на проводник с током в магнитном поле, обусловлена действием сил на отдельные движущиеся заряды, а уже от этих зарядов действие передается проводнику, по которому они перемещаются. Этот вывод подтверждается целым рядом опытных фактов и, в частности, тем, что пучок свободно летящих заряженных частиц, например электронный пучок, отклоняется магнитным полем.

Согласно (46.4) на элемент тока d l действует в магнитном поле сила

d f = i d l ´ B (47.1)

Заменив i d l через S j d l, выражению закона Ампера можно придать вид

d f = S d l j ´ B = j ´ B d V

где d V – объем проводника, к которому приложена сила d f. Разделив d f на d V, получим «плотность силы», т. е. силу, действующую на единицу объема проводника:

f _ед.об = j ´ B (47.2)

Подставив в эту формулу j = en u, найдем, что

f _ед.об = n е ' u ´ В.

Эта сила равна сумме сил, приложенных к носителям, заключенным в единице объема. Таких носителей n, следовательно, на один носитель действует сила, равная f _ед.об/ n = е ' u ´ В.

Таким образом, можно утверждать, что на заряд е', движущийся со скоростью u в магнитном поле В, действует сила

f = е ' u ´ В (47.3)

Силу (47.3) называют силой Лоренца.

Часто лоренцевой силой называют сумму электрической и магнитной сил, действующих на заряд:

f = е ' E + е ' u ´ В

Модуль лоренцевой силы равен

f = e ' uB sin a (47.5)

где a – угол между векторами u и B. Следовательно, заряд, движущийся вдоль линий магнитного поля, не испытывает действия силы.

Направлена сила Лоренца перпендикулярно к плоскости, в которой лежат векторы u и B. Если заряд е ' положителен, направление силы совпадает с направлением вектора u ´ В.

Рис. 86

В случае отрицательного е направления векторов f и u ´ В противоположны (рис. 86).

Поскольку сила Лоренца всегда направлена перпендикулярно к скорости заряженной частицы, она работы над частицей не совершает. Следовательно, действуя на заряженную частицу постоянным магнитным полем, изменить ее энергию нельзя.

При получении выражения. (47.3) для силы Лоренца из формулы (47.1) мы считали, что носители заряда в проводнике движутся со скоростью упорядоченного движения и. Однако даже в отсутствие тока носители заряда находятся в хаотическом тепловом движении. Среднее (по носителям) значение вектора скорости этого

движения u ₀ равно нулю: .

Поэтому и результирующая сил (47.3), действующих на носители, заключенные в элементе проводника d l, при отсутствии тока также равна нулю:

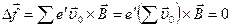(47.6)

При возникновении тока скорость носителя етаноится равной u = u ₀ + u. В этом случае

Первая сумма в этом выражении в соответствии с (47.6) равна нулю. Вторая сумма совпадает с (47.2 f _ед.об = j ´ B). Таким образом, действующая на ток амперова сила слагается из лоренцевых сил, обусловленных упорядоченным движением носителей заряда.

Сила, действующая на ток в магнитном поле, имеет значение (47.1 d f = i d l ´ B), независимо от того, покоится проводник с током или перемещается относительно магнитного поля. В этом легко убедиться, воспользовавшись выражением (47.3 f = е ' u ´ В) для силы Лоренца. Пусть провод, по которому течет ток, движется со скоростью v, а электрон, являющийся носителем заряда, имеет относительно провода скорость u. Тогда электрон движется относительно поля со скоростью u + u и на него будет действовать сила

f _ = – е (u + u) ´ В ] = – е u ´ В – е u ´ В,

а на участок провода – сила

d f _ = – е u ´ В d N – е u ´ В d N,

где d N – число электронов в элементе тока d l, а u – средняя скорость их движения относительно проводника.

Провод в целом нейтрален – он образован неподвижными положительными ионами и свободно движущимися электронами. Положительные ионы движутся вместе с проводом со скоростью u, так что на каждый из них действует сила

f ₊ = е u ´ В

Число ионов в элементе тока d l такое же, как число электронов. Следовательно, на ионы, содержащиеся в элементе d l, действует сила

d f ₊ = е u ´ В d N.

Элемент провода длины d l испытывает действие силы, равной сумме сил d f _+ d f ₊, которая, как легко видеть, имеет значение

d f = d f _+ d f ₊ = – е u ´ В d N

Полученное нами выражение эквивалентно формуле (47.1 d f = i d l ´ B). В него не входит скорость проводника u. Таким образом, закон Ампера имеет одинаковый вид и для покоящегося и для движущегося проводника.

Контур с током в магнитном поле. Действие момента сил на контур с током, сила, действующая на контур в неоднородном поле.

Пусть прямоугольный плоский контур с током помещается в однородном магнитном поле. Если контур ориентирован так, что вектор В параллелен его плоскости (рис. 87), то стороны, имеющие длину b, не будут испытывать действия сил, так как для них в формуле (46.5 d f =

Рис. 87.

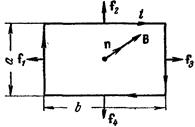Рис. 88.

= iВ d l sin a) sin a = 0. На левый участок будет согласно закону Ампера действовать сила f = iBa, направленная за чертеж, на правый участок– такая же по величине, но обратно направленная сила f '. Эти силы образуют пару, момент которой равен

М = f b = iBab.

Учитывая, что ab равно площади контура S, а iS есть величина магнитного момента p _m, можно написать

M = p _m В. (48.1)

Эта формула совпадает по существу с формулой (39.3 ).

Момент М стремится повернуть контур так, чтобы его магнитный момент р _m выстроился по направлению поля В. Такая ориентация контура показана на рис. 88.

В этом случае f ₁ = f ₃ = iBa, f ₂ = f ₄ = iBb. Направления всех сил лежат в плоскости контура. Видно, что вращательный момент в этом случае не возникает. Поскольку поле однородно, равнодействующая сил равна нулю; силы лишь растягивают контур, но сместить его не могут. Если повернуть контур на 180° (или изменить направление поля на обратное), то направления всех сил изменятся на противоположные, и они будут не растягивать, а сжимать контур.

Рис. 89

Покажем, что формула (48.1 M = p _m В) справедлива и для плоского контура произвольной формы. Разобьем площадь контура на узкие параллельные направлению вектора В полоски шириной d h (рис. 89, а). На элемент контура d l ₁ действует сила d f ₁ = iB d l ₁ sin a ₁, направленная за чертеж. На элемент d l ₂ действует сила d f ₂ = iB d l ₂ sin a ₂, имеющая противоположное направление. Как видно из рис. 89 б, d l ₁ sin a ₁ = d l ₂ sin a ₂ = dh, то есть ширине полоски. Следовательно, силы d f ₁ и d f ₂ одинаковы по величине и образуют пару, момент которой равен

d M = iB d h b,

где b – длина полоски. Произведение b ×d h дает площадь полоски d S. Таким образом,

d M = iB d S.

Беря попарно силы, приложенные к противолежащим элементам контура, и суммируя их моменты, получим результирующий момент, действующий на контур:

,

аналогичный формуле (48.1).

При произвольной ориентации контура (рис. 90) магнитную индукцию В можно разложить на составляющие: B _^ – перпендикулярную и В _|| – параллельную плоскости контура, и рассматривать действие каждой составляющей отдельно. Составляющая B _^ будет обусловливать силы, растягивающие или сжимающие контур.

Составляющая В _||, величина которой равна В sin a (a – угол между p _m и В), приведет к возникновению вращательного момента, который можно вычислить по формуле (48.1 M = p _m В):

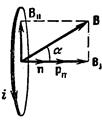Рис. 90.

M = p _m В _|| = p _m В sin a (48.2)

Принимая во внимание взаимную ориентацию векторов М, p _m и В, формулу (48.2) можно записать в виде

М = p _m´ В. (48.3)

Для того чтобы угол a между векторами p _m и В увеличить на d a, нужно совершить против сил, действующих на контур в поле, работу

d А = M d a = p _m B sin a d a. (48.5)

Поворачиваясь в нервоначальное положение, контур может возвратить затраченную на его поворот работу, совершив ее над какимй-либо телами. Следовательно, работа (48.5) идет на увеличение энергии W, которой обладает контур с током в магнитном поле,

d W = p _m B sin a d a.

Интегрируя, находим, что

W = – p _m B cos a + const.

Если положить const = 0, формула приобретает вид

W = – p _m B cos a = – p _m× В (48.6)

Отметим, что формула (48.6) аналогична выражению для энергии, которой обладает диполь в электрическом поле.

Теперь рассмотрим плоский контур с током в неоднородном магнитном поле. Для простоты будем вначале считать контур круговым. Предположим, что поле изменяется быстрее всего в направлении х, совпадающем с направлением В в том месте, где расположен центр контура, и что магнитный момент контура ориентирован вдоль поля (рис 91,а).

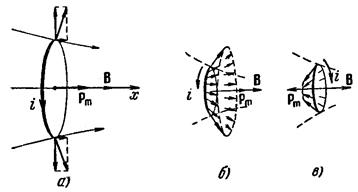Рис. 91.

Сила d f, действующая на элемент контура, перпендикулярна к В, т.е.к линии магнитной индукции в месте пересечения ее с d l. Поэтому силы, приложенные к различным элементам контура, образуют симметричный конический «веер» (рис. 91,6). Их результирующая f направлена в сторону возрастания В и, следовательно, втягивает контур в область более сильного поля. Очевидно, что чем сильнее изменяется поле (чем больше градиент 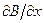поля, тем меньше угол раствора «веера» и тем больше, при прочих равных условиях, результирующая сила f. Если изменить направление тока в контуре на обратное (при этом p _m станет противоположным В), направления всех сил d f и их результирующей f изменятся на обратные (рис. 91,в). Следовательно, при такой взаимной ориентации векторов p _m и В контур будет выталкиваться из поля.

С помощью выражения (48.6) для энергии контура в магнитном поле легко найти количественное выражение для f. Если ориентация магнитного момента по отношению к полю остается неизменной (a = const), то W будет зависеть только от х (через В). Дифференцируя W по х и изменяя у результата знак, получим проекцию силы на ось х

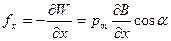
По предположению в других направлениях поле изменяется слабо, поэтому проекциями силы на другие оси можно пренебречь и считать, что f = f _x. Итак,

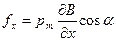(48.8)

Согласно полученной нами формуле сила, действующая на контур с током в неоднородном магнитном поле, зависит от ориентации магнитного момента контура относительно направления поля. Если векторы p _m и В совпадают по направлению (a = 0), сила положительна, т.е. направлена в сторону возрастания В (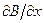 предполагается положительным; в противном случае знак и направление силы изменятся на противоположные, но сила по-прежнему будет втягивать контур в область сильного поля). Если p _m и В антипараллельны (a = p), сила отрицательна, т. е. направлена в сторону убывания В.

Этот результат мы уже получили качественно с помощью рис. 91.

Разумеется, кроме силы (48.8) на контур с током в неоднородном магнитном поле будет действовать также вращательный момент (48.3 М = p _m´ В).

Работа, совершаемая при перемещении тока в магнитном поле.

Допустим, что провод с током может свободно перемещаться во внешнем магнитном поле. Это можно осуществить с помощью скользящих контактов между концами провода и остальными участками замкнутой цепи (рис. 92). Внешнее поле будем предполагать однородным и перпендикулярным к плоскости контура. При указанных на рисунке направлениях тока и поля сила будет направлена вправо и равна f = iBl где l – длина перемещающегося участка тока. На пути d s эта сила совершит над проводником работу

d A = f d S = iBl d S

Произведение l d s равно заштрихованной площади (рис. 92), a Bl d S – потоку магнитной индукции d Ф через эту площадку. Поэтому можно написать, что

d A = i d Ф (49.1)

где d Ф – поток магнитной индукции, пересекаемый проводником при его движении.

Полученный нами результат легко обобщить на случай неоднородного поля. Для этого нужно разбить проводник на участки d l и сложить элементарные работы, совершаемые над

Рис. 92.

каждым участком (в пределах каждой малой площадки d l d s магнитную индукцию можно считать постоянной).

Если вектор В образует с нормалью к контуру угол a, отличный от нуля, направление силы составит с направлением перемещения также угол a (f перпендикулярна к В) и

d A = f cos a d s = iB _n l d s,

где B _n = В cos a – составляющая вектора В по направлению нормали к площадке l d s. Произведение B _n l d s есть d Ф – поток, пересекаемый проводником. Таким образом и в этом случае мы приходим к формуле (49.1).

Заметим, что работа (49.1) совершается не за счет магнитного поля (сила Лоренца работы над зарядами не совершает), а за счет источника, поддерживающего ток в контуре.

Далее будет показано, что при изменениях потока магнитной индукции, пронизывающего контур, в этом контуре возникает э. д. с. индукции 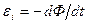. Следовательно, в этом случае источник тока, кроме работы, затрачиваемой на выделение ленц – джоулева тепла, должен совершать дополнительную работу против э. д. с. индукции, определяемую выражением

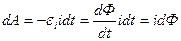
которое совпадает с (49.1).

Найдем работу, совершаемую над замкнутым контуром с током при его перемещении в магнитном поле. Вначале предположим, что контур, перемещаясь, остается все время в одной плоскости (рис. 93; вектор В направлен за чертеж). Силы, приложенные к участку контура 1–2, образуют с направлением перемещения острые углы. Следовательно, совершаемая ими работа А ₁ положительна. Согласно формуле (49.1 d A = i d Ф) эта работа пропорциональна силе тока в

Рис. 93

контуре i и пересеченному участком 1–2 потоку магнитной индукции. Участок 1–2 пересекает при своем движении поток Ф ₀ через заштрихованную поверхность и поток Ф_к, пронизывающий контур в его конечном положении.

Таким образом.

A ₁ = i (Ф ₀ + Ф _к)

Силы, действующиена участок контура 2–1, образуют с направлением перемещения тупые углы. Поэтому совершаемая ими работа А₂ отрицательна.

Абсолютная величина ее пропорциональна потоку, пересекаемому участком 2–1, который слагается из Ф ₀ и Ф_н – потока, пронизывающего контур в начальном положении. Следовательно,

A ₂ = i (Ф ₀ + Ф _н).

Работа, совершаемая над всем контуром, равна

А = А ₁ + А ₂ = i (Ф ₀ + Ф _к) – i (Ф ₀ + Ф _н) = i (Ф _к – Ф _н)

Разность магнитного потока через контур в конце перемещения Ф _к и потока в начале Ф _н дает приращение потока через контур D Ф. Таким образом,

А = i D Ф (49.2)

При выводе формулы (49.2) мы сделали определенные предположения о характере движения контура. Можно показать, что эта формула остается справедливой при любом движении контура в произвольном магнитном поле. В частности, при повороте контура в однородном поле из положения, в котором векторы р _m и В направлены в противоположные стороны, в положение, при котором эти векторы совпадают по направлению, силы поля совершают над контуром работу

A =2 iSB

(Ф _н = – BS, вектор В и положительная нормаль имеют противоположные направления, вследствие чего Ф _н отрицателен; Ф _к = BS). Учитывая, что iS = р _m – магнитному моменту контура, получаем

А = 2 p _m В.

Тот же результат получается с помощью выражения (48.6 W = – p _m× В) для энергии контура в магнитном поле:

А = W _н – W _к = p _m В – (– p _m В) = 2 p _m В.

Магнитное поле в веществе. Намагниченность.

Проводники, по которым текут токи, создающие магнитное поле, находятся в вакууме. Если несущие ток проводники находятся в какой–либо среде, магнитное поле существенным образом изменяется. Это объясняется тем, что всякое вещество является магнетиком, т. е. способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Намагниченное вещество создает магнитное поле В ', которое накладывается на обусловленное токами поле В ₀. Оба поля в сумме дают результирующее поле:

В = В ₀+ В ’ (43.1)

Истинное (микроскопическое) поле в магнетике сильно изменяется в пределах межмолекулярных расстояний. Под В подразумевается усредненное (макроскопическое) поле.

Для объяснения намагничения тел Ампер предположил, что в молекулах вещества циркулируют круговые токи. Каждый такой ток обладает магнитным моментом и создает в окружающем пространстве магнитное поле.

В отсутствие внешнего поля молекулярные токи ориентированы беспорядочным образом, вследствие чего обусловленное ими результирующее поле равно нулю. В силу хаотической ориентации магнитных моментов отдельных молекул суммарный магнитный момент тела также равен нулю. Под действием поля магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего магнетик намагничивается – его суммарный магнитный момент становится отличным от нуля. Магнитные поля отдельных молекулярных токов в этом случае уже не компенсируют друг друга и возникает поле В '.

Намагничение магнетика естественно характеризовать магнитным моментом единицы объема. Эту величину называют вектором намагничивания и обозначают J. Если магнетик намагничен неоднородно, вектор намагничения в данной точке определяется следующим выражением:

(43.2)

где D V –физически бесконечно малый объем, взятый в окрестности рассматриваемой точки, р _m – магнитный момент отдельной молекулы. Суммирование производится по всем молекулам, заключенным в объеме D V.

Описание поля в магнетиках. Напряженность поля. Магнитная восприимчивость и магнитная проницаемость.

Найдем поток вектора В = В ₀+ В ’ через произвольную замкнутую поверхность:

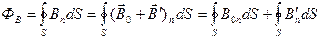
Как было установлено, что линии вектора В ₀ (характеризующего поле, создаваемое макроскопическими токами) всегда замкнуты. То же самое справедливо и для линий вектора В '. Поэтому оба интеграла, стоящие справа, равны нулю (каждая из линий В ₀ или В ' пересекает замкнутую поверхность четное число раз, причем она входит внутрь поверхности столько же раз, сколько выходит наружу). Следовательно,

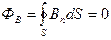(44.1)

Эта формула выражает теорему Гаусса для вектора В: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.

Теперь обратимся к циркуляции вектора В, которая по определению равна

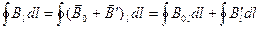
Ранее было установлено, что циркуляция вектора В ₀, выражаемая первым из интегралов, стоящих в правой части, пропорциональна алгебраической сумме макроскопических токов i, охватываемых контуром, по которому берется циркуляция. Аналогично циркуляция вектора В ' (второе слагаемое) должна быть пропорциональна сумме всех, охватываемых контуром молекулярных токов i _m. Следовательно, циркуляция вектора В результирующего поля пропорциональна сумме всех охватываемых контуром токов (как макроскопических i, так и молекулярных i _m,):

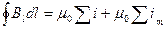(44.2)

Возникает ситуация, аналогичная той, с которой мы столкнулись при рассмотрении электрического поля в диэлектриках [см. формулу A6.2)]: для того чтобы определить В, нужно

Рис. 77.

знать не только токи, текущие по проводам, но и молекулярные токи. Путь, позволяющий обойти это затруднение – введение величины, аналогичной вектору электрического смещения. Можно найти такую вспомогательную величину, которая связана простым соотношением с вектором В _n определяется лишь макроскопическими токами.

Чтобы установить вид этой вспомогательной величины, попробуем выразить фигурирующую в (44.2) сумму молекулярных токов через вектор намагничения магнетика J. В эту сумму должны войти только те молекулярные токи, которые оказываются «нанизанными» на контур, для которого вычисляется циркуляция. Как видно из рис. 77, элемент контура d l, образующий с направлением намагничения угол a, пересекает те молекулярные токи, центры которых попадают внутрь косого цилиндра с объемом SM cos a d l (SM – площадь, охватываемая отдельным молекулярным током). Если n – число молекул в единице объема, то суммарный ток, охватываемый элементом d l, равен i _m nS _mcos a d l. Произведение i _m S _m равно магнитному моменту р _m отдельного молекулярного тока. Следовательно, выражение i _m nS _m представляет собой магнитный момент единицы объема, т. е. дает модуль вектора J, a i _m nS _mcos a – проекцию i _l вектора J на направление элемента d l. Таким образом, суммарный молекулярный ток, охватываемый элементом d l, равен i _ld l, а сумма молекулярных токов, охватываемых всем контуром:

Дата добавления: 2015-04-24