Взаимодействие токов. 7 страница

Таким образом, квантовая теория объясняет с единой точки зрения существование хороших проводников (металлов), полупроводников и изоляторов.

Рассмотрим распределение электронов по уровням зоны проводимости в металле. При абсолютном нуле на каждом из N /2 нижних уровней будет находиться по два электрона, остальные уровни будут свободны. Такое распределение показано на рис. 138 сплошной линией. По оси ординат отложено число электронов на данном уровне [смысл обозначения 2f(W) станет ясен в дальнейшем]. В качестве индекса для обозначения уровня использована его энергия W. Собственно, в соответствии с тем, что уровни энергии дискретны, распределение изображается слева от W _max совокупностью точек с ординатой 2, а справа от W _max – точками с ординатой 0. Но так как расстояния между уровнями очень малы, эти точки располагаются весьма густо и образуют сплошную линию.

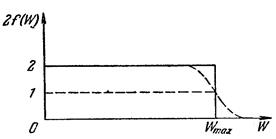Рис. 138.

Для верхнего заполненного при абсолютном нуле уровня квантовая теория дает значение

где ħ = 1,05 ×10^-34 дж×сек, m – масса электрона, n – число свободных электронов в единице объема. Принимая n = 10²⁹ м³, получим

Если бы уровни зоны распределялись по оси энергии с постоянной плотностью (т. е. число уровней d z, приходящееся на интервал энергий d W, не зависело от W), среднее значение энергии электронов было бы равно половине максимального. В действительности плотность уровней пропорциональна 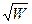, т. е. d z ~ 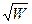d W. Вычисления дают для средней энергии электронов при абсолютном нуле значение 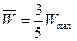. Следовательно, даже при 0°К электроны проводимости в металле обладают огромной кинетической энергией, равной в среднем примерно 5 эв. Чтобы сообщить классическому электронному газу такую энергию, его нужно нагреть до температуры порядка шестидесяти тысяч градусов Кельвина.

Столь же быстро движутся и валентные электроны в изоляторах. Однако они находятся в таких условиях, что электрическое поле не может изменить их состояние и вызвать преобладание движения в одном направлении.

Выясним, какова вероятность нахождения электронов на различных уровнях при температурах, отличных от 0 К. В классической физике распределение частиц по состояниям с различной энергией характеризуется функцией Больцмана:

(71.1)

где А – коэффициент пропорциональности. Эта функция определяет вероятность того, что частица будет находиться в состоянии с энергией W.

Распределение (71.1) было получено в предположении, что в каждом состоянии с данной энергией может находиться неограниченное количество частиц. Более того, при Т = 0 функция (71.1) обращается в нуль при всех значениях энергии, кроме W = 0. Это означает, что все частицы должны находиться на нулевом уровне.

Функция распределения, учитывающая принцип запрета Паули, была найдена Ферми. Она имеет вид

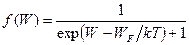(71.2)

Здесь W – энергия данного уровня, W_F – параметр системы, называемый уровнем Ферми.

Функция (71.2) дает вероятность заполнения электронами данного уровня. Легко убедиться в том, что сплошная кривая на рис. 138 с точностью до множителя 2 совпадает с графиком функции (71.2) для Т = 0. В самом деле, в этом случае

f (W) = 1, если W < W _F

и

f (W) = 0, если W > W _F

Таким образом, при 0 К уровень Ферми совпадает с верхним заполненным электронами уровнем W _max.

Для W = W _F функция (71.2) при любой ненулевой температуре имеет значение, равное ½. Следовательно, уровень Ферми совпадает с тем энергетическим уровнем, вероятность заполнения которого равна половине (на таком уровне в среднем находится один электрон). Значение W _F можно найти из условия

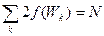(71.3)

где N– полное число валентных электронов в кристалле. Каждое слагаемое представляет собой среднее число электронов на k –м уровне. Суммирование производится по всем уровням валентной зоны и остальных лежащих над ней зон.

Уровни в пределах разрешенных зон лежат очень густо. Поэтому сумму (71.3) можно заменить интегралом. Всем уровням, лежащим в пределах небольшого интервала энергий d W, можно приписать одинаковую занятость 2 f (W). Если плотность уровней равна g (W), число их в интервале d W составит g(W)d W. На долю этих уровней придется в среднем

d N _W = 2 f (W) g (W)d W

электронов. А полное число электронов на всех уровнях должно быть равно

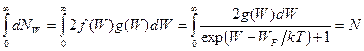(71.4)

Зная вид g (W), можно вычислить интеграл (71.4) (для интервалов энергий, соответствующих запрещенным зонам, g (W) следует положить равной нулю). Получившееся выражение будет содержать W _F и Т. Следовательно, для данного N можно найти W _F как функцию Т. Выражение (71.4) представляет собой по существу условие нормировки функции f (W).

Вычисления, проведенные для металлов, показывают, что W _F слабо зависит от температуры, так что значения уровня Ферми при не слишком высоких температурах (если kT << W _F0) мало отличаются от значения W _F0 при абсолютном нуле.

При температурах, отличных от 0 К, распределение, описываемое функцией (71.2), имеет вид, показанный на рис. 138 пунктирной кривой. Ордината кривой характеризует среднюю по времени занятость уровня, поэтому, например, ордината, равная 0,25, означает, что ¼ времени уровень занят одним электроном (или 1/8 – двумя), а остальное время пустует.

В области больших энергий (т. е. при W – W _F >> kT, что выполняется в области «хвоста» кривой распределения) единицей в знаменателе можно пренебречь.

Тогда функция (71.2) принимает вид

(71.5)

т. e. переходит, в функцию (71.1) распределения Больцмана.

Распределение электронов по уровням можно сделать очень наглядным, изобразив, как это сделано на рис. 139, кривую распределения Ферми совместно со схемой энергетических зон.

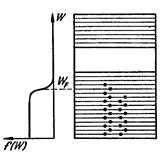Рис 139.

Чем выше температура, тем более полого идет ниспадающий участок кривой. Однако заметное отличие распределения при температуре Т от распределения при 0° К наблюдается лишь в области порядка kT. Следовательно, тепловое движение влияет на кинетическую энергию лишь небольшой части всех электронов. Поэтому средняя энергия электронов слабо зависит от температуры. Этим объясняется тот факт, что электроны проводимости не вносят заметного вклада в теплоемкость металла. Таким образом, квантовая теория устраняет одно из основных затруднений, которого не могла преодолеть классическая теория.

Для зависимости электропроводности металла от температуры квантовая теория также дает хорошо согласующиеся с опытом результаты.

Полупроводники

Полупроводники обязаны своим названием тому обстоятельству, что по величине электропроводности они занимают промежуточное положение между металлами и изоляторами. Однако характерным для них является не величина проводимости, а то, что их проводимость растет с повышением температуры (напомним, что у металлов она уменьшается). Полупроводниками являются вещества, у которых валентная зона полностью заполнена электронами (см. рис. 137,6), а ширина запрещенной зоны невелика (у собственных полупроводников не более 1 эв).

Различают собственную и примесную проводимости полупроводников.

Собственная проводимость. Собственная проводимость возникает в результате перехода электронов с верхних уровней валентной зоны в зону проводимости. При этом в зоне проводимости появляется некоторое число носителей тока – электронов, занимающих уровни вблизи дна зоны; одновременно в валентной зоне освобождается такое же число мест на верхних уровнях. Такие свободные от электронов места на уровнях заполненной при абсолютном нуле валентной зоны называют дырками.

Распределение электронов по уровням валентной зоны и зоны проводимости определяется функцией Ферми (71.2).

Рис. 140.

Вычисления по формуле (71.4) показывают, что уровень Ферми лежит точно посредине запрещенной зону (рис. 140). Следовательно, для электронов, перешедших в зону проводимости, величина W – W _F мало отличается от половины ширины запрещенной зоны. Уровни зоны проводимости лежат на хвосте кривой распределения. Поэтому вероятность их заполнения электронами можно находить по формуле (71.5). Полагая в этой формуле W – W _F = D W /2, получим

(72.1)

Количество электронов, перешедших в зону проводимости, будет пропорционально вероятности (72.1). Эти электроны, а также, как мы увидим ниже, образовавшиеся в таком же числе дырки, являются носителями тока. Поскольку проводимость пропорциональна числу

Рис.141.

носителей, она также должна быть пропорциональна выражению (72.1). Следовательно, электропроводность полупроводников быстро растет с температурой, изменяясь по закону

(72.2)

где D W – ширина запрещенной зоны.

Если на графике откладывать зависимость ln s от 1/ T, то для полупроводников получается прямая линия, изображенная на рис. 141. По наклону этой прямой можно определить ширину запрещенной зоны D W.

Типичными полупроводниками являются элементы IV группы периодической системы Менделеева – германий и кремний. Они образуют решетку, в которой каждый атом связан ковалентными связями с четырьмя равноотстоящими от него соседними атомами. Условно такое взаимное расположение атомов можно представить в виде плоской структуры, изображенной на рис. 142. Кружки со знаком «+» обозначают положительно заряженные атомные остатки (т. е. ту часть атома, которая остается после удаления валентных электронов), кружки со знаком «–» – валентные электроны, двойные линии – ковалентные связи.

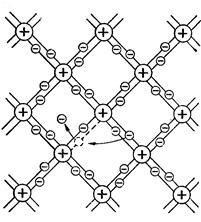Рис. 142.

При достаточно высокой температуре тепловое движение может разорвать отдельные пары, освободив один электрон (такой случай показан на рис. 142). Покинутое электроном место перестает быть нейтральным, в его окрестности возникает избыточный положительный заряд (+ е) – образуется дырка. На это место может перескочить электрон одной из соседних пар. В результате дырка начинает также странствовать по кристаллу, как и освободившийся электрон. Если свободный электрон встретится с дыркой, они рекомбинируют (соединяются).

Это означает, что электрон нейтрализует избыточный положительный заряд, имеющийся в окрестности дырки, и теряет свободу передвижения до тех пор, пока снова не получит от кристаллической решетки энергию, достаточную для своего высвобождения. Рекомбинация приводит к одновременному исчезновению свободного электрона и дырки. На схеме уровней (рис. 140) процессу рекомбинации соответствует переход электрона из зоны проводимости на один из свободных уровней валентной зоны.

Итак, в полупроводнике идут одновременно два процесса: рождение попарно свободных электронов и дырок и рекомбинация, приводящая к попарному исчезновению электронов и дырок. Вероятность первого процесса быстро растет с температурой. Вероятность рекомбинации пропорциональна как числу свободных электронов, так и числу дырок. Следовательно, каждой температуре соответствует определенная равновесная концентрация электронов и дырок, величина которой изменяется.с температурой по такому же закону, как и s [см. (72.2)].

В отсутствие внешнего электрического поля электроны проводимости и дырки движутся хаотически. При включении поля на хаотическое движение накладывается упорядоченное движение электронов против поля и дырок – в направлении поля. Оба движения – и дырок, и электронов – приводят к переносу заряда вдоль кристалла. Следовательно, собственная электропроводность определяется носителями заряда двух знаков – отрицательными электронами и положительными дырками.

Собственная проводимость наблюдается во всех без исключения полупроводниках при достаточно высокой температуре.

Примесная проводимость. Этот вид проводимости возникает, если некоторые атомы данного полупровод ника заменить в узлах кристаллической решетки атомами, валентность

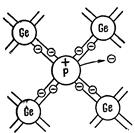Рис. 143.

которых отличается на единицу от валентности основных атомов. На рис. 143 условно изображена решетка германия с примесью 5–валентных атомов фосфора. Для образования ковалентных связей с соседями атому фосфора достаточно четырех электронов. Следовательно, пятый валентный электрон оказывается лишним и легко отщепляется от атома за счет энергии теплового движения, образуя странствующий свободный электрон. В отличие от рассмотренного раньше случая образование свободного электрона не сопровождается нарушением ковалентных связей, т. е. образованием дырки. Хотя в окрестности атома примеси возникает избыточный положительный заряд, но он связан с этим атомом и перемещаться по решетке не может. Благодаря этому заряду атом примеси может захватить приблизившийся к нему электрон, но связь захваченного электрона с атомом будет непрочной и легко нарушается вновь за счет тепловых колебаний решетки.

Таким образом, в полупроводнике с 5–валентной примесью имеется только один вид носителей тока – электроны. Соответственно говорят, что такой полупроводник обладает электронной проводимостью или является полупроводником n–типа (от слова negativ – отрицательный). Атомы примеси, поставляющие электроны проводимости, называются донорами.

Примеси искажают поле решетки, что приводит к возникновению на энергетической схеме так называемых локальных уровней, расположенных в запрещенной зоне кристалла (рис. 144). Любой уровень валентной зоны или зоны проводимости может быть занят электроном, находящимся в любом месте кристалла.

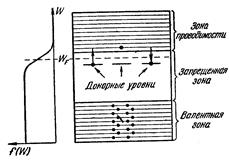Рис. 144.

Энергию, соответствующую локальному уровню, электрон может иметь, лишь находясь вблизи атома примеси, вызвавшего появление этого уровня. Следовательно, электрон, занимающий примесный уровень, расположен (локализован) вблизи атома примеси.

Если донорные уровни расположены недалеко от потолка валентной зоны, то есть пятый электрон прочно связан со своим атомом, они не могут существенно повлиять на электрические свойства кристалла. Иначе обстоит дело, когда расстояние таких уровней от дна зоны проводимости гораздо меньше, чем ширина запрещенной зоны. В этом случае энергия теплового движения даже при обычных температурах оказывается достаточной для того, чтобы перевести электрон с донорного уровня в зону проводимости. На рис. 143 этому процессу соответствует отщепление пятого электрона от атома примеси. Захвату свободного электрона атомом примеси соответствует на рис. 144 переход электрона из зоны проводимости на один из донорных уровней.

Уровень Ферми в полупроводнике n – типа лежит между донорными уровнями и дном зоны проводимости, при невысоких температурах – приблизительно посредине между ними (рис. 144).

На рис. 145 условно изображена решетка кремния с примесью 3–валентных атомов бора. Трех валентных электронов атома бора недостаточно для образования связей со всеми

Рис. 145.

четырьмя соседями. Поэтому одна из связей окажется не заполненной и будет представлять собой место, способное захватить электрон. При переходе на это место электрона одной из соседних пар возникнет дырка, которая будет кочевать по кристаллу.

Вблизи атома примеси возникнет избыточный отрицательный заряд, но он будет связан с данным атомом и не может стать носителем тока. Таким образом, в полупроводнике с 3–валентной примесью возникают носители тока только одного вида – дырки. Проводимость в этом случае называется дырочной, а о полупроводнике говорят, что он принадлежит к р–типу (от слова positiv – положительный). Примеси, вызывающие возникновение дырок, называются акцепторными.

На схеме уровней (рис. 146) акцептору соответствует расположенный в запретной зоне недалеко от ее дна локальный уровень. Образованию дырки отвечает переход электрона из валентной зоны на акцепторный уровень. Обратный переход соответствует разрыву одной из четырех ковалентных связей атома примеси с его соседями и рекомбинации образовавшегося при этом электрона и дырки.

Уровень Ферми в полупроводнике р–типа лежит между потолком валентной зоны и акцепторными уровнями, при невысоких температурах – приблизительно посредине между ними. С повышением температуры концентрация примесных носителей тока быстро достигает насыщения. Это означает, что практически освобождаются все донорные или заполняются

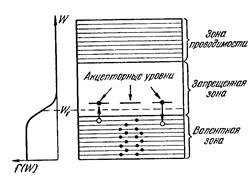Рис. 146.

электронами все акцепторные уровни. Вместе с тем по мере роста температуры все в большей степени начинает сказываться собственная проводимость полупроводника, обусловленная переходом электронов непосредственно из валентной зоны в зону проводимости.

Таким образом, при высоких температурах проводимость полупроводника будет складываться из примесной и собственной проводимости. При. низких температурах преобладает примесная, а при высоких–собственная проводимость.

Эффект Холла

Холл обнаружил в 1880 г. следующее явление: если металлическую пластинку, вдоль которой течет постоянный электрический ток, поместить в перпендикулярное к ней магнитное поле, то между параллельными току и полю гранями (рис. 147) возникает разность потенциалов U _H = j ₁ – j ₂. Величина ее определяется выражением

U _H = RbjB (73.1)

где b – ширина пластинки, j – плотность тока, B – магнитная индукция поля, R – разный для различных металлов коэффициент пропорциональности, получивший название

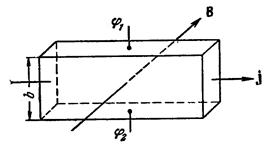Рис. 148.

Рис. 148

постоянной Холла. Само явление называют эффектом Холла или гальваномагнитным явлением.

Эффект Холла очень просто объясняется электронной теорией. В отсутствие магнитного поля ток в пластинке обусловливается электрическим полем Е ₀ (рис. 148). Эквипотенциальные поверхности этого поля образуют систему перпендикулярных к вектору Е ₀ плоскостей, изображенных на рисунке сплошными прямыми линиями.

Потенциал во всех точках каждой поверхности, а следовательно, и в точках 1 и 2 одинаков. Носители тока – электроны – имеют отрицательный заряд, поэтому скорость их упорядоченного движения и направлена противоположно вектору плотности тока j. При включении магнитного поля каждый носитель оказывается под действием силы Лоренца, направленной вдоль стороны b пластинки (рис, 147) и равной по модулю

f = euB (73.2)

В результате у электронов появляется составляющая движения в направлении к верхней (на рисунке) грани пластинки. У этой грани образуется избыток отрицательных, соответственно у нижней грани – избыток положительных зарядов. Следовательно, возникает дополнительное поперечное электрическое поле Е _B. Когда напряженность этого поля достигает такой величины, что его действие на заряды будет уравновешивать силу (73.2), установится стационарное распределение зарядов в поперечном направлении. Соответствующее значение Е _B определяется из условия: еЕ _B = еuВ, откуда

Е _B = uВ (73.3)

Поле Е _B складывается с полем Е ₀ в результирующее поле Е. Эквипотенциальные поверхности перпендикулярны в каждой точке к вектору напряженности поля. Следовательно, они повернутся и займут положения, изображенные на рис. 148 пунктиром. Точки 1 и 2, которые прежде лежали на одной и той же эквипотенциальной поверхности, теперь будут иметь разные потенциалы.

Чтобы найти напряжение, возникающее между этими точками, нужно умножить Е _B на расстояние между ними b. Выражая, кроме того, в (73.3) u через j, n и е в соответствии с формулой j = neu, получим

(73.4)

Последнее выражение совпадает с (73.1), если положить

R = 1/ ne (73.5)

Таким образом, измерив постоянную Холла, можно найти концентрацию носителей тока (т. е. их число в единице объема).

Важной характеристикой вещества является подвижность в нем носителей тока, под которой подразумевается средняя скорость, приобретаемая носителем в поле, напряженность которого равна единице. Если в поле напряженности Е носители приобретают скорость u, то подвижность их m равна

m = u / E (73.6)

В СИ скорость измеряется в метрах в секунду, напряженность электрического поля в вольтах на метр. Следовательно, единицей подвижности будет 1 м²×в^-1×сек^-1.

Рис. 149.

Подвижность можно связать с проводимостью s и концентрацией носителей n. Для этого разделим соотношение j = neu на напряженность поля Е. Учтя, что отношение j к Е дает s, а u, деленное на Е, есть подвижность, получим

s = nem G3.7)

Определив постоянную Холла R и проводимость s, можно по формулам (73.5) и (73.7) найти концентрацию и подвижность носителей тока в соответствующем образце.

Явление Холла наблюдается не только в металлах, но и в полупроводниках, причем по знаку эффекта можно судить о принадлежности полупроводника к n– или р–типу. На рис. 149 сопоставлен эффект Холла для образцов с положительными и отрицательными носителями. Направление силы Лоренца изменяется на противоположное как при изменении направления движения заряда, так и при изменении его знака. Следовательно, при одинаковом направлении тока сила Лоренца, действующая на положительные и отрицательные носители, имеет одинаковое направление. Поэтому в случае положительных носителей потенциал верхней (на рисунке) грани выше, чем нижней, а в случае отрицательных носителей – ниже. Таким образом, определив знак холловской разности потенциалов, можно установить знак носителей тока.

Любопытно, что у некоторых металлов знак U _H соответствует положительным носителям тока. Это объясняется особым перекрыванием зон, при котором часть электронов переходит с верхних уровней валентной зоны на нижние уровни другой зоны. В результате возникают в равном количестве как свободные электроны, так и дырки. Проводимость такого металла имеет смешанный (электронно–дырочный) характер. Аномальный (для металлов) знак эффекта Холла обусловлен тем, что дырки обладают большей подвижностью, чем электроны.

Работа выхода

Металлы не приобретают заряда сами по себе. Значит, электроны проводимости не могут самопроизвольно покидать металл в заметном количестве. Это объясняется тем, что металл представляет для электронов потенциальную яму. Покинуть металл удается только тем электронам, энергия которых оказывается достаточной для преодоления потенциального барьера, имеющегося на поверхности. Силы, обусловливающие этот барьер, имеют следующее происхождение.

Случайное удаление электрона от наружного слоя положительных ионов решетки приводит к возникновению в том месте, которое покинул электрон, избыточного положительного заряда. Кулоновское взаимодействие с этим зарядом заставляет электрон, скорость которого не очень велика, вернуться обратно. Таким образом, отдельные электроны все время покидают поверхность металла, удаляются от нее на несколько межатомных расстояний и затем возвращаются обратно. В результате металл оказывается окруженным тонким облаком электронов. Это облако образует совместно с наружным слоем ионов двойной электрический слой (рис. 150; кружки – ионы, черные точки – электроны). Силы, действующие на электрон в таком слое, направлены внутрь металла. Работа, совершаемая против этих сил при выходе электрона из металла наружу, идет на увеличение потенциальной энергии электрона W _p.

Таким образом, потенциальная энергия валентных электронов внутри металла меньше, чем вне металла, на величину, равную глубине потенциальной ямы W _p0 (рис. 151). Скачок потенциальной энергии происходит на длине порядка нескольких межатомных расстояний

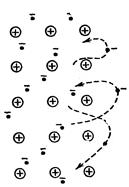Рис. 150.

Рис. 151.

(~10^{-9 м), поэтому стенки ямы можно считать вертикальными.}

Потенциальная энергия электрона связана с потенциалом точки, в которой находится электрон, соотношением W _p = – ej. Поскольку заряд электрона отрицателен, потенциал точки и потенциальная энергия электрона имеют разные знаки. Отсюда следует, что потенциал внутри металла больше, чем потенциал в непосредственной близости к его поверхности (мы будем для краткости говорить просто «на поверхности»), на величину W _p0/e.

Сообщение металлу избыточного положительного заряда увеличивает потенциал как на поверхности, так и внутри металла. Потенциальная энергия электрона соответственно уменьшается (рис. 152,а). На рис. 152,6 даны кривые W _p и j для случая, когда металл заряжен отрицательно. В этом случае высота потенциального барьера немного понижается (соответственно уменьшается работа выхода). Это явление называется эффектом Шоттки.

Полная энергия электронов в металле слагается из потенциальной и кинетической энергий. Как было выяснено, значения кинетической энергии электронов проводимости заключены при абсолютном нуле в пределах от 0 до совпадающей с уровнем Ферми W _max. На рис. 153

Рис. 152.

энергетические уровни зоны проводимости вписаны в потенциальную яму (пунктиром изображены незанятые при 0°К уровни). Для удаления за пределы металла разным электронам

Рис. 153.

нужно сообщить неодинаковую энергию. Так, электрону, находящемуся на самом нижнем уровне зоны проводимости, необходимо сообщить энергию W _р0, для электрона, находящегося на уровне Ферми, достаточна энергий W _p0 – W _max = W _р0 – W _F.

Наименьшая энергия, которую необходимо сообщить электрону для того, чтобы удалить его из твердого тела в вакуум, называется работой выхода. Работу выхода принято обозначать через еj, где j – величина, имеющая размерность потенциала и называемая потенциалом выхода.

В соответствии со сказанным выше работа выхода электрона из металла определяется выражением

еj = W _p0 – W _F (74.1)

Мы пришли к этому выражению в предположении, что температура металла равна 0 К. При других температурах работу выхода также определяют как разность глубины потенциальной ямы и уровня Ферми, т. е. распространяют определение (74.1) на любые температуры. Это же определение применяется и для полупроводников.

Дата добавления: 2015-04-24