Взаимодействие токов. 4 страница

Рис. 96

или молекулы пучка должна действовать сила

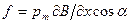
величина и знак которой зависят от угла a, образуемого вектором р _m с направлением поля. При хаотическом распределении моментов молекул по направлениям в пучке имеются частицы, для которых значения a изменяются в пределах от 0 до p.

В соответствии с этим предполагалось, что узкий молекулярный пучок после прохождения

Рис. 97.

между полюсами оставит на экране сплошной растянутый след, края которого соответствуют молекулам, с ориентациями под углами a = 0 и p (рис. 97). Опыт дал неожиданные результаты.

Вместо сплошного растянутого следа получались отдельные линии, расположенные симметрично относительно следа пучка, полученного в отсутствии поля. Опыт Штерна и Герлаха показал, что углы, под которыми магнитные моменты атомов и молекул ориентируются по отношению к магнитному полю, могут иметь лишь дискретные значения, т. е. что проекции магнитного момента на направление поля квантуются.

Число возможных значений проекции магнитного момента на направление магнитного поля для разных атомов различно. Для атомов серебра, алюминия, меди и щелочных металлов оно равно двум, для ванадия, азота и галогенов – четырем, для кислорода – пяти, для марганца – шести, железа – девяти, кобальта – десяти и т. д.

Для магнитных моментов атомов измерения дали значения порядка нескольких магнетонов Бора. Некоторые атомы не обнаружили отклонения (см., например, след атомов ртути и магния на рис. 97), что указывает на отсутствие у них магнитного момента.

Диамагнетизм. Ларморова прецессия.

Электрон, движущийся по орбите, подобен волчку. Поэтому ему должны быть свойственны все особенности поведения гироскопов под действием внешних сил, в частности при соответствующих условиях должна возникать прецессия электронной орбиты. Условия, необходимые для прецессии, осуществляются, если атом находится во внешнем магнитном поле В (рис. 98). В этом случае на орбиту действует вращательный момент М = p _m´ B, стремящийся установить орбитальный магнитный момент электрона p _m по направлению поля (при этом механический момент L установится против поля).

Под действием момента М векторы L и p _m совершают прецессию вокруг направления вектора магнитной индукции В, скорость которой легко найти.

За время dt вектор L получает приращение d L, равное

d L = M d t

Вектор d L, как и вектор М, перпендикулярен к плоскости, проходящей через векторы В и L, и по модулю равен

|d L | = p _m В sin a d t,

где a – угол между p _m и В. За время d t плоскость, в которой лежит вектор L, повернется вокруг направления В на угол

Разделив этот угол на время d t, найдем угловую скорость прецессии.

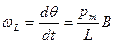
Подставив в это выражение значение (51.3) отношения магнитного и механического орбитальных моментов электрона, получим

w _L = eB /2 m (52.1)

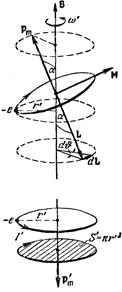Рис. 98.

Частоту w _L называют частотой ларморовой прецессии или просто ларморовой частотой. Она не зависит ни от угла наклона орбиты по отношению к направлению магнитного поля, ни от радиуса орбиты или скорости электрона и, следовательно, для всех электронов, входящих в состав атома, одинакова.

Прецессия орбиты обусловливает дополнительное движение электрона вокруг направления поля. Если бы расстояние r ' электрона от параллельной В оси, проходящей через центр орбиты, не изменялось, дополнительное движение электрона происходило по окружности радиуса r ' (см. незаштрихованную окружность в нижней части рис. 98). Ему соответствовал бы круговой ток (см. заштрихованную окружность) магнитный момент которого

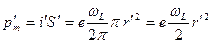(52.2)

направлен, как видно из рис. 98, в сторону, противоположную В. Этот момент называется индуцированным (наведенным) магнитным моментом.

В действительности, вследствие движения электрона по орбите расстояние r ' все время меняется. Поэтому в формуле (52.2) нужно брать вместо r '² его среднее по времени значение . Это среднее зависит от угла a, характеризующего ориентацию плоскости орбиты по отношению к В. В частности, для орбиты, перпендикулярной к вектору В, r ' постоянно и равно

Рис. 99

радиусу орбиты r. Для орбиты, плоскость которой проходит через направление В, r ' изменяется по закону r ' = r sin wt, где w – угловая скорость обращения электрона по орбите (рис. 99; вектор В и орбита лежат в плоскости рисунка). Следовательно, 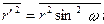и, поскольку среднее значение квадрата синуса есть ½ .

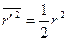Если произвести усреднение по всем возможным значениям a, считая их равновероятными, то получается

(52.3)

В атомах со многими электронами орбиты ориентированы всевозможными способами, поэтому каждому электрону можно приписать в среднем значение (52.3). Подставив в (52.2) значение (52.1) для w _L и (52.3) для 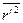, получим для среднего значения индуцированного магнитного момента одного электрона следующее выражение:

(52.4)

(знак «–» отражает то, что векторы p ’_m и В направлены в противоположные стороны).

Мы предполагали орбиту круговой. В противном случае (например, для эллиптической орбиты) вместо r ² нужно взять 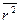, т. е. средний квадрат расстояния электрона от ядра.

Просуммировав выражение (52.4) по всем электронам, найдем индуцированный магнитный момент атома в целом:

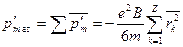(52.5)

(число электронов в атоме равно, как известно, атомному номеру Z).

Итак, под действием внешнего магнитного поля происходит прецессия электронных орбит с одинаковой для всех электронов угловой скоростью (52.1). Обусловленное прецессией дополнительное движение электронов приводит к возникновению индуцированного магнитного момента атома (52.5), направленного против поля. Ларморова прецессия возникает у всех без исключения веществ. Однако в тех случаях, когда атомы обладают сами по себе магнитным моментом, магнитное поле не только индуцирует момент (52.5), но и оказывает на магнитные моменты атомов ориентирующее действие, устанавливая их по направлению поля. Возникающий при этом положительный (т. е. направленный вдоль поля) магнитный момент бывает значительно больше, чем отрицательный индуцированный момент. Поэтому результирующий момент оказывается положительным и вещество ведет себя как парамагнетик.

Диамагнетизм обнаруживают лишь те вещества, у которых атомы не обладают магнитным моментом (векторная сумма орбитальных и спиновых магнитных моментов электронов атома равна нулю). Если для.такого вещества умножить равенство (52.5) на число Авогадро N _A, получится магнитный момент килограмм-атома вещества. Разделив его на напряженность поля Н, найдем килограмм-атомную магнитную восприимчивость c_кат. Относительная магнитная проницаемость диамагнетиков практически равна 1. Поэтому можно положить В / Н = m ₀.

Таким образом,

(52.6)

Радиусы электронных орбит имеют величину порядка 10^–10 м. Следовательно, согласно (52.6) килограмматомная диамагнитная восприимчивость получается порядка 10^–8¸10^–7, что хорошо согласуется с экспериментальными данными.

Парамагнетизм.

Если магнитный момент р _m атомов отличен от нуля, вещество оказывается парамагнитным. Внешнее магнитное поле стремится установить магнитные моменты атомов вдоль В, тепловое движение стремится разбросать их равномерно по всем направлениям. В результате устанавливается некоторая равновесная преимущественная ориентация моментов вдоль поля тем большая, чем больше В, и тем меньшая, чем выше температура.

Кюри экспериментально установил закон, согласно которому парамагнитная килограмм-атомная восприимчивость вещества равна

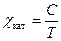(53.1)

где С – постоянная Кюри, зависящая от рода вещества, Т – абсолютная температура.

Классическая теория парамагнетизма была развита Ланжевеном в 1905 г. Мы ограничимся изложением этой теории для случая не слишком сильных полей и не очень низких температур.

Согласно формуле (48.6) атом обладает в магнитном поле потенциальной энергией W = – p _m B cos q, которая зависит от угла q между векторами p _m и В. Поэтому равновесное распределение моментов по направлениям должно подчиняться закону Больцмана. Согласно этому закону вероятность того, что магнитный момент атома будет образовывать с направлением вектора В угол, заключенный в пределах от q до q +d q, пропорциональна

exp(– W / kT) = exp(p _m B cos q / kT).

Введя обозначение

a = p _m B / kT (53.2)

выражение, определяющее вероятность, можно записать в виде exp(a cos q).

Будем изображать направления магнитных моментов атомов с помощью точек на сфере единичного радиуса. Если бы поле не оказывало на магнитные моменты ориентирующего действия, они были бы распределены по направлениям хаотически. В этом случае плотность точек на сфере постоянна и равна n /4 p, где n – количество рассматриваемых атомов, которое мы возьмем равным числу атомов в единице объема. Поэтому число атомов, моменты которых образуют с направлением В углы, заключенные в пределах от q до q +d q, было бы равно (рис. 100)

(53.3)

Рис. 100

В действительности, магнитное поле оказывает на моменты ориентирующее действие, в результате чего направления с меньшими q становятся преобладающими. Вероятность различных ориентации, как мы видели, пропорциональна exp(a cos q). Следовательно, чтобы получить распределение моментов по направлениям при наличии магнитного поля, нужно выражение (53.3) умножить на этот множитель:

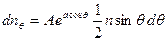(53.4)

(A – неизвестный пока коэффициент пропорциональности).

Магнитный момент атома имеет величину порядка одного магнетона Бора, т.е. ~ 10^–23 Дж/Тл. При достигаемых обычно полях магнитная индукция бывает порядка 1 Тл. Следовательно, р _m В имеет порядок 10^–23 дж. Величина kT при комнатной температуре равна примерно 4×10^–21 дж. Таким образом, а = p _m B / kT << 1 exp(a cos q) можно заменить приближенно через 1 + acos q. В этом приближении выражение (53.4) принимает вид:

Константу А можно найти, воспользовавшись тем, что полное число молекул, имеющих все возможные ориентации, характеризуемые значениями q от 0 до p, должно быть равно n:

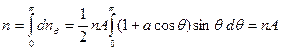
Отсюда А = 1, так что

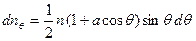
Магнитные моменты атомов распределяются симметрично относительно направления поля. Поэтому результирующий магнитный момент совпадает по направлению с В. Следовательно, каждый атом вносит в результирующий момент вклад, равный p _mcos q. Таким образом, для магнитного момента единицы объема (т. е. для вектора намагничения) можно написать следующее выражение:

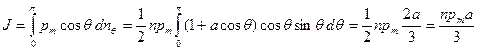
Подставляя сюда вместо а его значение (53.2), получаем

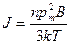
Наконец, разделив J на H, найдем восприимчивость

(53.5)

(для парамагнетиков также можно положить B / H = m ₀)

Взяв вместо n число Авогадро N _A, получим выражение для килограмм-атомной восприимчивости

(53.6)

Легко видеть, что мы пришли к закону Кюри.

Напомним, что формула E3.6) получена в предположении, что р _m В << kT. В очень сильных полях и при низких температурах наблюдаются отступления от пропорциональности между намагничением парамагнетика J и напряженностью поля H, в частности, может наступить состояние магнитного насыщения, при котором все р _m выстраиваются по полю, и дальнейшее увеличение H не приводит к возрастанию J.

Значения c_кат, рассчитанные по формуле (53.6), в ряде случаев хорошо согласуются со значениями, получаемыми из опыта.

Квантовая теория парамагнетизма учитывает то обстоятельство, что возможны лишь дискретные ориентации магнитного момента атома относительно поля. Она приводит к выражению для c_кат, аналогичному (53.6).

Ферро и антиферромагнетизм. Доменная структура.

Особый класс магнетиков образуют вещества, способные обладать намагничением даже в отсутствие внешнего магнитного поля. По своему наиболее распространенному представителю – железу – они получили название ферромагнетиков. К их числу принадлежат железо, никель, кобальт, гадолиний, их сплавы и соедивения, а также некоторые сплавы и соединения марганца и хрома с неферромагнитными элементами (например, MnAlCu, СгТе и т. д.). В последнее время большую роль стали играть ферромагнитные полупроводники, называемые ферритами. Ферромагнетизм присущ всем этим веществам только в кристаллическом состоянии.

Ферромагнетики являются сильномагнитными веществами– их намагничение в огромное (до 10¹⁰) число раз превосходит намагничение диа- и парамагнетиков, принадлежащих к категории слабомагнитных веществ.

Намагничение слабомагнитных веществ изменяется с напряженностью поля линейно. Намагничение ферромагнетиков зависит от Н сложным образом. На рис. 101 дана кривая намагничения ферромагнетика, магнитный момент которого первоначально был равен нулю

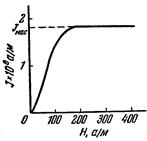Рис. 101.

Рис. I02.

(она называется основной или нулевой кривой намагничения). Уже в полях порядка ~ 100 а/м намагничение J достигает насыщения. Основная кривая намагничения на диаграмме В– Н приведена на рис. 102 (кривая 0–1). Напомним, что В = m ₀ (Н + J). Поэтому по достижении насыщения В продолжает расти с Н по линейному закону: В = m ₀ Н + const, где const = m ₀ J _нас.

Приятно отметить, что кривая намагничения железа была впервые получена и подробно исследована русским ученым А. Г. Столетовым.

Кроме нелинейной зависимости между Н и J (или Н и В) для ферромагнетиков характерно также наличие гистерезиса. Если довести намагничение до насыщения (точка 1 на рис. 102) и затем уменьшать напряженность магнитного поля, то намагничение следует не первоначальной кривой 0–1, а изменяется в соответствии с кривой 1–2. В результате, когда напряженность внешнего поля станет равной нулю (точка 2), намагничение не исчезает и характеризуется величиной В _r, которая называется остаточной индукцией. Намагничение имеет при этом значение J _r, называемое остаточным намагничением.

Намагничение обращается в нуль (точка 5) лишь под действием поля Н _с, имеющего направление, противоноложное полю, вызвавшему намагничение. Напряженность Нс называется коэрцитивной силой. Существование остаточного намагничения делает возможным изготовление постоянных магнитов, т. е. тел, которые без затраты энергии на поддержание макроскопических токов обладают магнитным моментом и создают в окружающем их пространстве магнитное поле.

Очевидно, что постоянный магнит тем лучше сохраняет свои свойства, чем больше коэрцитивная сила материала, из которого он изготовлен. При действии на ферромагнетик переменного магнитного поля индукция изменяется в соответствии с кривой 1–2–3–4–5–1 (рис. 102), которая называется петлей гистерезиса (аналогичная петля получается и на диаграмме J – Н). Если максимальные значения Н таковы, что намагничение достигает насыщения, получается так называемая максимальная петля гистерезиса (сплошная петля на рис. 102). Если при амплитудных значениях Н насыщение не достигается, получается петля, называемая частным циклом (пунктирная петля на рисунке). Частных циклов может существовать бесконечное множество, все они лежат внутри максимальной петли гистерезиса.

Гистерезис приводит к тому, что намагничение ферромагнетика не является однозначной функцией Н; оно в сильной мере зависит также от предшествующей истории образца – от того, в каких полях он побывал прежде.

Так, например, в поле напряженности Н ₁ (рис. 102) индукция может иметь любое значение в пределах от В ₁’ до В ₁".

Из всего сказанного о ферромагнетиках видно, что они очень похожи по своим свойствам на сегнетоэлектрики. В связи с неоднозначностью зависимости В от Н понятие магнитной проницаемости применяется лишь к основной кривой намагничения. Относительная магнитная проницаемость ферромагнетиков m, (а следовательно и магнитная восприимчивость

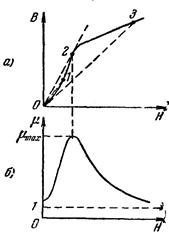Рис. 103

c) является функцией напряженности поля. На рис. 103, а изображена основная кривая намагничения. Проведем из начала координат прямую линию, проходящую через произвольную точку кривой. Тангенс угла наклона этой прямой пропорционален отношению В / Н, т.е. относительной магнитной проницаемости m для соответствующего значения напряженности поля. При увеличении Н от нуля угол наклона (а значит и m) сначала растет. В точке 2 он достигает максимума (прямая 0–2 является касательной к кривой), а затем убывает. На рис. 103,6 дан график зависимости m от Н. Из рисунка видно, что максимальное значение проницаемости достигается несколько раньше, чем насыщение. При неограниченном возрастании Н проницаемость асимптотически приближается к единице. Это следует из того, что J в выражении m = 1 + J / H не может превысить значение J _нас.

Величины B _r (или J _r), Н _с и m _max являются основными характеристиками ферромагнетика. Если коэрцитивная сила не велика, ферромагнетик называется жестким. Для него характерна

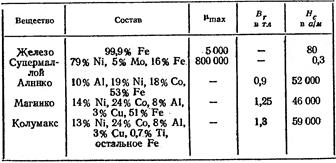
широкая петля гистерезиса. Ферромагнетик с малой Нс (и соответственно узкой петлей гистерезиса) называется мягким. В зависимости от назначения берутся ферромагнетики с той или иной характеристикой. Так, для постоянных магнитов употребляются жесткие ферромагнетики, а для сердечников трансформаторов – мягкие. В таблице приведены характеристики некоторых типичных ферромагнетиков.

Ферромагнетики при намагничении деформируются. Это явление называется магнитострикцией. Относительное изменение линейных размеров образца при магнитострикции невелико –- в полях порядка 105 а/м оно составляет 10^–5–10^–6. Знак эффекта зависит от природы ферромагнетика, ориентации кристаллографических осей по отношению к направлению магнитного поля и от напряженности поля. У некоторых ферромагнетиков при переходе от слабых полей к сильным знак магнитострикции изменяется на обратный.

Теория ферромагнетизма была создана Я- И. Френкелем и В. Гейзенбергом в 1928 г. Из опытов по изучению магнитомеханических явлений (см. § 51) следует, что ответственными за магнитные свойства ферромагнетиков являются собственные (спиновые) магнитные моменты

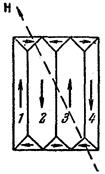Рис. 104.

электронов. При определенных условиях в кристаллах могут возникать так называемые обменные силы (природа этих сил сугубо квантовая и рассмотрение их в данном разделе невозможно). Обменное взаимодействие заставляет магнитные моменты электронов выстраиваться параллельно друг другу. В результате возникают области спонтанного (самопроизвольного) намагничения, которые называются также доменами.

В пределах каждого домена ферромагнетик спонтанно намагничен до насыщения и обладает определенным магнитным моментом. Направления этих моментов для разных доменов различны (рис. 104),так что в отсутствие внешнего поля суммарный момент всего тела равен нулю. Домены имеют размеры порядка 10^-6– 10^{-5 м.}

Действие поля на домены на разных стадиях процесса намагничения оказывается различным. Вначале, при слабых полях, наблюдается смещение границ доменов, в результате чего происходит увеличение тех доменов, моменты которых составляют с Н меньший угол, за счет доменов, у которых угол между векторами р _m и Н больше. Например, домены 1 и 3 (рис. 104) увеличиваются за счет доменов 2 и 4. С увеличением напряженности поля этот процесс идет все дальше и дальше, пока домены с меньшими углами, обладающие в магнитном поле меньшей энергией, не поглотят целиком энергетически менее выгодные домены. На следующей стадии имеет место поворот магнитных моментов доменов в направлении поля. При этом моменты электронов в пределах домена поворачиваются одновременно, без нарушения их строгой параллельности друг другу. Эти процессы (исключая небольшие смещения границ между доменами в очень слабых полях) являются необратимыми, что и служит причиной гистерезиса.

Для каждого ферромагнетика имеется определенная температура Т _с, при которой области спонтанного намагничения распадаются и вещество утрачивает ферромагнитные свойства. Эта температура называется точкой Кюри. Для железа она равна 768° С, для никеля 365° С. При температуре выше точки Кюри ферромагнетик становится обычным парамагнетиком, магнитная восприимчивость которого подчиняется закону Kюри – Вейсса

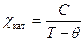(54.1)

Величина q носит название температуры Вейса и определяется величиной обменного взаимодействия и величиной магнитного момента отдельного магнитного атома магнетика. При охлаждении ферромагнетика ниже точки Кюри в нем снова возникают домены.

В точке Кюри присходит фазовый переход второго рода. При температуре, равной Т _с, наблюдается аномалия в поведении ряда физических свойств, в частности теплоемкости, ферромагнетика.

В некоторых случаях обменные силы приводят к возникновению так называемых антиферромагнетиков (хром, марганец и др.).

В антиферромагнетиках собственные магнитные моменты электронов самопроизвольно ориентированы антипараллельно друг другу. Такая ориентация охватывает попарно соседние атомы. В результате антиферромагнетики обладают крайне малой магнитной восприимчивостью и ведут себя как очень слабые парамагнетики.

Для антиферромагнетиков также существует температура T _n (аналог температуры Кюри в случае ферромагнетиков), при которой антипараллельная ориентация спинов исчезает. Эта температура называется антиферромагнитной точкой Кюри или точкой Нееля. У некоторых антиферромагнетиков (например, у эрбия, диспрозия, сплавов марганца и меди) таких температур две (верхняя и нижняя точки Нееля), причем антиферромагнитные свойства наблюдаются только при промежуточных температурах. Выше верхней точки вещество ведет себя как парамагнетик, а при температурах, меньших нижней точки Нееля, становится ферромагнетиком.

Явление электромагнитной индукции.

В 1831 г. Фарадей открыл, что во всяком замкнутом проводящем контуре при изменении потока магнитной индукции через поверхность, ограниченную этим контуром, возникает электрический ток. Это явление называют электромагнитной индукцией, а возникающий ток индукционным.

Рис. 105.

Величина индукционного тока не зависит от способа, которым вызывается изменение потока магнитной индукции Ф, но определяется лишь скоростью изменения Ф, т. е. значением d Ф /d t. При изменении знака d Ф /d t меняется также направление тока. Поясним сказанное следующим примером. На рис. 105 изображен контур 1, силу тока в котором i ₁ можно менять с помощью реостата. Ток i ₁ создает магнитное поле, пронизывающее контур 2. Если увеличивать ток i ₁ поток магнитной индукции Ф через контур 2 будет расти. Это приведет к появлению в контуре 2 индукционного тока i ₂, регистрируемого гальванометром. Уменьшение тока i ₁ обусловит убывание потока магнитной индукции через второй контур, что приведет к появлению в нем индукционного тока иного направления, чем в первом случае. Индукционный ток i ₂ можно вызвать также, приближая контур 2 к первому контуру, или удаляя второй контур от первого. В обоих случаях направления возникающего тока будут противоположными. Наконец, электромагнитную индукцию можно вызвать, не перемещая контур 2 поступательно, а поворачивая его так, чтобы менялся угол между нормалью к контуру и направлением поля.

Заполнение всего пространства, в котором поле отлично от нуля, однородным магнетиком приводит, при прочих равных условиях, к увеличению индукционного тока в m раз. Этим подтверждается то, что индукционный ток обусловлен изменением не потока вектора Н, а потока магнитной индукции.

Ленц установил правило, с помощью которого можно найти направление индукционного тока. Правило Ленца гласит, что индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей. Если, например, изменение Ф вызвано перемещением контура, то возникает индукционный ток такого направления, что сила, действующая на него во внешнем поле, противится движению контура. При приближении контура 2 к первому контуру возникает ток i ₂ (рис. 105), магнитный момент которого направлен против внешнего поля (угол a между векторами р _m и В равен p). Следовательно, согласно формуле (48.8) на контур 2 будет действовать сила, отталкивающая его от первого контура. При удалении контура 2 от первого контура возникает ток i ₂", момент которого р _m совпадает по направлению с В (a = 0), так что сила, действующая на контур 2, имеет направление к первому контуру.

Дата добавления: 2015-04-24