Взаимодействие токов. 1 страница

Электрические токи взаимодействуют между собой. Например, два тонких прямолинейных параллельных проводника, по которым текут токи (мы будем называть их прямыми токами), притягивают друг друга, если токи в них имеют одинаковое направление, и взаимно отталкиваются, если направление токов противоположное.

Опыт показывает, что сила взаимодействия, приходящаяся на единицу длины каждого из параллельных проводников, пропорциональна величинам токов в них i ₁ и i ₂ и обратно пропорциональна расстоянию b между ними:

(38.1)

По соображениям, которые станут ясными в дальнейшем, коэффициент пропорциональности мы обозначили через 2 k.

Закон взаимодействия токов был установлен в 1820 г. Ампером. Общий вид этого закона будет записан далее. § 46.

На основании закона (38.1) устанавливается единица силы тока в системе СИ. Единица силы тока в СИ – ампер – определяется как сила неизменяющегося тока, который, проходя по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызвал бы между этими проводниками силу, равную 2×10^–7 Н на каждый метр длины.

Кулон определяют как заряд, проходящий за 1 сек через поперечное сечение проводника, по которому течет постоянный ток силой в 1 а. В рационализованном виде формула (38.1) записывается следующим образом:

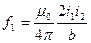(38.2)

где m ₀ – так называемая магнитная постоянная. Чтобы найти численное значение m ₀ воспользуемся тем, что согласно определению ампера при i ₁ = i ₂ = 1 а и b = 1 м f ₁ получается равной 2×10^–7 Н/м. Подставим эти значения в формулу (38.2):

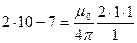
Отсюда

Магнитное поле.Магнитный момент.

Взаимодействие токов осуществляется через поле, которое называется магнитным. Это название происходит от того, что, как обнаружил в 1820 г. Эрстед, поле, создаваемое током, оказывает ориентирующее действие на магнитную стрелку.

Движущиеся заряды (токи) изменяют свойства окружающего их пространства – создают в нем магнитное поле. Это поле проявляется в том, что на движущиеся в нем заряды (токи) действуют силы.

Подобно тому, как для исследования электрического поля мы использовали пробный точечный заряд, применим для исследования магнитного поля пробный ток, циркулирующий в плоском замкнутом контуре очень малых размеров. Ориентацию контура в пространстве будем характеризовать направлением нормали к контуру, связанной с направлением тока правилом правого винта (рис. 63). Такую нормаль мы будем называть положительной.

Рис 63

Внеся пробный контур в магнитное поле, мы обнаружим, что поле оказывает на контур ориентирующее действие, устанавливая его положительной нормалью в определенном направлении. Примем это направление за направление поля в данной точке. Если контур повернуть так, чтобы направления нормали и поля не совпадали, возникает вращательный момент, стремящийся вернуть контур в равновесное положение. Величина момента зависит от угла a между нормалью и направлением поля, достигая наибольшего значения М _mах при a = p/2 (при a = 0 момент равен нулю).

Вращательный момент зависит как от свойств поля в данной точке, так и от свойств контура. Внося в одну и ту же точку разные пробные контуры, мы обнаружим, что величина М _mах пропорциональна силе тока I в контуре и площади контура S и совершенно не зависит от формы контура Таким образом, действие магнитного поля на плоский контур с током определяется величиной

p _m = IS, (39.1)

которую называют магнитным моментом контура (аналогично вращательный момент, действующий в электрическом поле на диполь, пропорционален электрическому моменту диполя р = ql).

Кроме силы тока I и площади S, контур характеризуется также ориентацией в пространстве. Поэтому магнитный момент следует рассматривать как вектор, направление которого совпадает с направлением положительной нормали:

p _m = p _m n

(n – единичный вектор).

На пробные контуры, отличающиеся значением p _m, действуют в данной точке поля разные по величине вращательные моменты М _mах. Однако отношение М _mах/ p _m будет для всех контуров одно и то же и может быть принято для количественной характеристики поля. Физическую величину В, пропорциональную этому отношению, называют магнитной индукцией:

(39.3)

Магнитная индукция – вектор, направление которого определяется равновесным направлением положительной нормали к пробному контуру (мы назвали его направлением поля). Формула (39.3) определяет модуль вектора В.

Поле вектора В можно представить наглядно с помощью линий магнитной индукции, которые строятся по тем же правилам, что и линии вектора Е.

Из сказанного вытекает, что В характеризует силовое действие магнитного поля на ток и, следовательно, является аналогом напряженности электрического поля Е, которая характеризует силовое действие электрического поля на заряд.

З-н Био-Савара. Поле движущегося заряда.

Био и Савар провели в 1820 г. исследование магнитных полей токов различной формы. Они установили, что магнитная индукция во всех случаях пропорциональна силе тока, создающего магнитное поле, и более или менее сложным образом зависит от расстояния до той точки, в которой определялась В. Лаплас проанализировал экспериментальные данные, полученные Био и Саваром, и нашел, что магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей,создаваемых отдельными элементарными участками тока. Для магнитной индукции поля, создаваемого моментом тока длины d l, Лаплас получил формулу

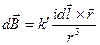(40.1)

где k ' – коэффициент пропорциональности, зависящий от выбора единиц измерения, i –.сила тока, d l – вектор, совпадающий с элементарным участком тока и направленный в ту сторону, в которую течет ток (рис. 64), r – вектор, проведенный от элемента тока в ту точку, в

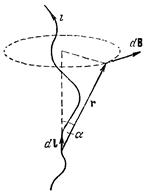Рис. 64

которой определяется d B, r – модуль этого вектора.

Соотношение (40.1) носит название закона Био – Савара – Лапласа или более кратко закона Био – Савара.

Направлен вектор d B перпендикулярно к плоскости, проходящей через d l и точку, в которой вычисляется поле, причем так, что вращение вокруг d l в направлении d B связано с d l правилом правого винта (рис 64). Для модуля d B можно написать следующее выражение:

(40.2)

где a – угол между векторами d l и r.

В рационализованной форме закон Био – Савара записывается следующим образом:

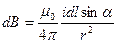(40.3)

т. е. полагается 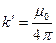. Единица магнитной индукции в СИ называется тесла (Тл).

Электрический ток есть, как мы знаем, упорядоченное движение зарядов. Таким образом, магнитное поле возбуждается движущимися зарядами. Поле (40.1) создается всеми движущимися зарядами, заключенными в элементе тока d l. Чтобы найти магнитную индукцию поля, создаваемого одним движущимся зарядом, преобразуем выражение (40.1), заменив в нем силу тока i произведением плотности тока j на площадь поперечного сечения проводника S. Вектор плотности тока j и вектор d l имеют одинаковое направление. Поэтому можно написать, что

i d l = S j d l. (40.6)

Если все носители заряда в проводнике одинаковы и имеют заряд е' (е' – алгебраическая величина), вектор плотности тока можно представить в виде [см. (31.4)]

j = е ' n u, (40.7)

где n – число носителей в единице объема, u – средняя скорость их упорядоченного движения. Заметим, что когда носители тока положительны, j и u имеют одинаковое направление. В случае отрицательных носителей j и u направлены в противоположные стороны.

Подставим в формулу (40.1) выражение (40.6) для id l, заменив в нем j согласно (40.7) (полагаем 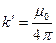). В результате получим, что

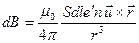(40.8)

Произведение Sn d l дает число носителей заряда, заключенных в элементе провода длины d l. Разделив выражение (40.8) на это число, получим магнитную индукцию поля, создаваемого одним зарядом, движущимся со скоростью u.

Если заряд е ' движется со скоростью u, то индукция создаваемого этим зарядом магнитного поля в точке, положение которой относительно заряда определяется радиусом-вектором r, равна

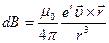(40.9)

Следует иметь в виду, что электромагнитные возмущения распространяются в пространстве с конечной скоростью, равной скорости света с. Поэтому поле в данной точке пространства будет соответствовать тому состоянию (т. е. положению и скорости) заряда, которое существовало на t = r /с секунд раньше (r –расстояние от точки, где был заряд раньше на t секунд, до точки, в которой определяется В). Таким образом, имеет место запаздывание значений поля, тем большее, чем дальше отстоит данная точка поля от вызвавшего это поле заряда. Формула (40.9) даёт правильный результат лишь в том случае, если перемещением заряда за время t (которое равно ut) можно пренебречь по сравнению с растоянием r до данной точки поля, т. е. при соблюдении условия: ut << r. Разделив неравенство на t и приняв во внимание, что r / t равно с, получим условие

u << c (40.11)

при котором справедлива формула (40.9).

Поле прямого и кругового токов.

Применим формулу (40.3) для вычисления полей простейших токов. Рассмотрим поле, создаваемое током, текущим по бесконечному прямому проводу (рис. 65). Все d B в данной точке имеют одинаковое направление (в нашем случае за чертеж). Поэтому сложение векторов d B можно заменить сложением их модулей. Точка, для которой мы вычисляем магнитную индукцию, находится на расстоянии b от провода. Из рис. 65 видно, что

Подставим эти значения в формулу (40.3 ):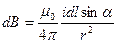

Угол a для всех элементов бесконечного прямого тока изменяется в пределах от 0 до p. Следовательно,

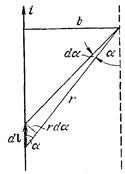Рис. 65.

Риг. 66.

Таким образом, магнитная индукция поля прямого тока определяется формулой

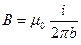(41.1)

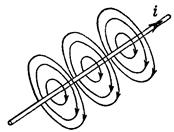
Линии магнитной индукции поля прямого тока представляют собой систему охватывающих провод концентрических окружностей (рис. 66).

Рис. 67.

Рис. 68

Рассмотрим поле, создаваемое током, текущим по тонкому проводу, имеющему форму окружности радиуса R (круговой ток). Определим магнитную индукцию в центре круговсго тока (рис. 67). Каждый элемент тока создает в центре индукцию, направленную вдоль положительной нормали к контуру. Поэтому векторное сложение d B сводится к сложению их модулей. По формуле (40.3 )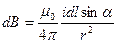

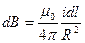
(a = p/2). Проинтегрируем это выражение по всему контуру:

Итак, магнитная индукция в центре кругового тока равна

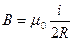(41.4)

Теперь найдем В на оси кругового тока, на расстоянии х от плоскости, в которой лежит контур (рис. 68).

Векторы d B перпендикулярны к плоскостям, проходящим через соответствующие d l и r. Следовательно, они образуют симметричный конический веер (рис. 68,6).

Из соображений симметрии можно заключить, что результирующий вектор В направлен вдоль оси тока. Каждый из составляющих векторов d B вносит в результирующий вектор вклад

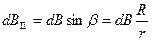
Угол a между d l и r прямой, поэтому

Проинтегрировав по всему контуру и заменив r на получим

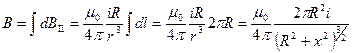(41.5)

При х = 0 эта формула переходит, как и должно быть, в формулу (41.4) для магнитной индукции в центре кругового тока.

Стоящее в числителе соотношения (41.5) выражение pR ² i равно р _m – магнитному моменту контура. На больших расстояниях от контура в знаменателе можно пренебречь R ² по сравнению с х ². Тогда формула (41.5) принимает вид

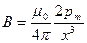
аналогичный выражению F.2) для напряженности электрического поля на оси диполя. Учитывая, что В на оси кругового тока и р _m направлены вдоль положительной нормали к контуру, можно написать

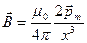(41.6)

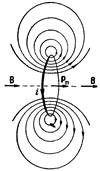Рис. 69.

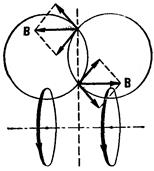Рис. 70

На рис. 69 изображены линии магнитной индукции поля кругового тока. Даны лишь линии, лежащие в одной из плоскостей, проходящих через ось тока. Подобная же картина имеет место в любой из этих плоскостей. Из рис. 70 видно, что два одинаковых соосных круговых тока создают в плоскости, относительно которой они симметричны, магнитную индукцию, направленную в каждой точке перпендикулярно к этой плоскости.

Циркуляция вектроа В. Поле соленоида.

Возьмем контур, охватывающий прямой ток, и вычислим для него циркуляцию вектора В:

.

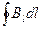Вначале рассмотрим случай, когда контур лежит в плоскости, перпендикулярной к току (рис. 71; ток перпендикулярен к плоскости чертежа и направлен за чертеж).

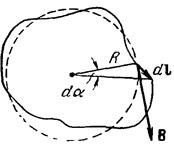Рис. 71.

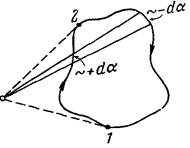Рис. 72.

В каждой точке контура вектор В направлен по касательной к окружности, проходящей через эту точку. Воспользовавшись известным свойством скалярного произведения векторов, B _ld l можно заменить через B d l _B, где d l_B – проекция перемещения d l на направление В. Но d l_B можно представить в виде R d a, где R – расстояние от прямого тока до d l, d a – угол, на который поворачивается радиальная прямая при перемещении вдоль контура на отрезок d l. Поэтому, учтя выражение (41.1 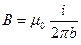) для В, можно написать

Таким образом, выражение для циркуляции имеет вид

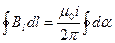(42.1)

При обходе по контуру, охватывающему ток, радиальная прямая все время поворачивается в одном направлении, поэтому 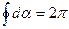. Иначе обстоит дело, если ток не охватывается контуром (рис. 72). В этом случае при обходе по контуру радиальная прямая поворачивается

Рис. 73.

сначала в одном направлении (участок 1–2), а затем в противоположном (участок 2–1), вследствие чего .

Учитывая этот результат, можно написать

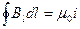(42.2)

где под i следует подразумевать ток, охватываемый контуром. Если контур тока не охватывает, циркуляция вектора В равна нулю.

Случай контура произвольной формы (рис. 73) отличается от рассмотренного нами случая лишь тем, что при перемещении вдоль контура радиальная прямая не только поворачивается вокруг тока, но и перемещается вдоль него. Все предыдущие выкладки остаются справедливыми, если под d a подразумевать угол, на который поворачивается проекция радиальной прямой на перпендикулярную к току плоскость. Суммарный угол поворота этой проекции равен 2 p, если контур охватывает ток, и нулю в противном случае. Следовательно, мы снова приходим к формуле (42.2). Эта формула получена нами для случая прямого тока. Можно показать, что она справедлива и для тока, текущего по проводнику произвольной формы.

Если контур охватывает несколько токов, циркуляция В равна их алгебраической сумме:

(42.3)

Вычисляя сумму токов, положительным нужно считать такой ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления будет отрицательным.

Выражение (42.3) справедливо только для поля в вакууме. Для поля в веществе в формуле (42.3), кроме токов, текущих по проводам (макротоков), необходимо учитывать также молекулярные токи.

Воспользовавшись соотношением (31.3 ), можно написать

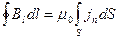(42.4)

где S – произвольная поверхность, опирающаяся на данный контур.

Величины Е и В являются основными силовыми характеристиками соответствующих полей. Сопоставление выражений (9.2) и (42.3) для циркуляции Е и В позволяет заключить, что между этими полями имеется принципиальное различие. Циркуляция напряженности электростатического поля всегда равна нулю, откуда следует, что электростатическое поле потенциально и может быть охарактеризовано потенциалом j. Циркуляция магнитной индукции отлична от нуля, если контур, по которому берется циркуляция, охватывает ток. Поля, обладающие таким свойством, называются вихревыми (или соленоидальными). Магнитному полю нельзя приписать потенциал, который был бы связан с магнитной индукцией соотношением, аналогичным формуле (11.7 ).

Этот потенциал не был бы однозначным – после каждого обхода по контуру,

Рис. 74.

охватывающему ток, и возвращения в первоначальную точку он получал бы приращение, равное m ₀ i.

Далее, линии напряженности электростатического поля начинаются и заканчиваются на зарядах. Как показывает опыт, линии магнитной индукции, напротив, всегда замкнуты (см. рис. 66, 69 и 75). Это указывает на то, что магнитных зарядов в природе не существует.

Применим формулу (42.3) для вычисления магнитной индукции поля бесконечно длинного соленоида. Соленоид (рис. 74) представляет собой тонкий провод, навитый плотно, виток к витку, на цилиндрический каркас. В отношении создаваемого им поля соленоид эквивалентен системе одинаковых круговых токов с общей прямой осью. Бесконечно длинный соленоид симметричен относительно любой перпендикулярной к его оси плоскости. Взятые попарно симметричные относительно такой плоскости витки создают поле, магнитная индукция которого перпендикулярна к плоскости (см. рис. 70). Следовательно, в любой точке внутри и вне соленоида вектор В может иметь лишь направление, параллельное оси.

Возьмем прямоугольный контур 1–2–3–4 (рис.74). Циркуляцию В по этому контуру можно представить следующим образом:

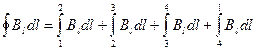
Из четырех интегралов, стоящих в правой части, второй и четвертый равны нулю, так как вектор В перпендикулярен к участкам контура, по которым они берутся.

Взяв участок 3–4 на большом расстоянии от соленоида (где поле заведомо должно быть очень слабым), третьим слагаемым можно пренебречь. Следовательно, можно утверждать, что

здесь В – магнитная индукция поля в тех точках, где располагается отрезок 1–2, l – длина этого отрезка.

Если отрезок 1–2 проходит внутри соленоида на любом расстоянии от его оси, контур охватывает суммарный ток nli, где n – число витков соленоида, приходящееся на единицу его длины, i – сила тока в соленоиде.

Поэтому согласно (42.3)

откуда

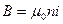(42.6)

Отметим, что полученный нами результат не зависит от того, на каком расстоянии от оси (но внутри соленоида) располагается отрезок 1–2. Если этот отрезок располагается вне соленоида, то охватываемый контуром ток равен нулю, вследствие чего

откуда B = 0. Таким образом, вне бесконечно длинного соленоида магнитная индукция равна нулю, внутри–всюду одинакова и имеет величину, определяемую формулой (42.6). По этой причине в учении о магнетизме бесконечно длинный соленоид играет такую же роль, как плоский конденсатор в учении об электричестве.

В обоих случаях поле однородно и полностью заключено внутри конденсатора (электрическое) и внутри соленоида (магнитное). Произведение in называется числом ампер-витков на метр. При n = 1000 витков на метр и силе тока в 1 а магнитная индукция внутри соленоида будет 4p×10^–4Тл.

Подобно тому, как оба круговых тока на рис. 70 вносят одинаковый вклад в результирующее поле, обе половины бесконечно длинного соленоида принимают равное участие в создании поля (42.6). Поэтому, если половину соленоида убрать, то у конца оставшегося «полубесконечного» соленоида магнитная индукция будет равна половине значения, получаемого из (42.6):

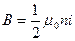(42.8)

Практически, если длина соленоида значительно больше, чем его диаметр, формула (42.6) будет справедлива для точек в средней части соленоида, а формула (42.8) для точек вблизи его

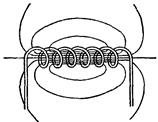Рис. 75.

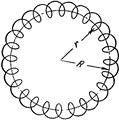Рис. 76.

концов.

На рис. 75 показана примерная картина линий магнитной индукции для соленоида конечной длины.

Тороид представляет собой тонкий провод, плотно навитый на каркас, имеющий форму тора (рис. 76). Он эквивалентен системе одинаковых круговых токов, центры которых расположены по окружности. Возьмем контур в виде окружности радиуса r, центр которой совпадает с центром тороида. В силу симметрии вектор В в каждой точке должен быть направлен по касательной к контуру. Следовательно,

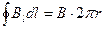
где В – магнитная индукция в тех точках, где проходит контур.

Если контур проходит внутри тороида, он охватывает ток 2 pRni (R– радиус тороида, n – число битков на единицу его длины). В этом случае

В 2 p r = m ₀2 pRni,

откуда

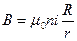(42.9)

Контур, проходящий вне тороида, токов не охватывает, поэтому для него В 2 p r = 0. Таким образом, вне тороида магнитная индукция равна нулю.

Для тороида, радиус которого R значительно превосходит радиус витка, отношение R / r для всех точек внутри тороида мало отличается от единицы и вместо (42.9) получается такая же формула, как для бесконечно длинного соленоида:

В = m ₀ ni (42.10)

В этом случае поле можно считать однородным в каждом из сечений тороида. В разных сечениях поле имеет различное направление, поэтому говорить об однородности поля в пределах всего тороида можно только условно, имея в виду модуль вектора В.

Сила, действующая на ток в магнитном поле. Сила Ампера для дифференциации силы и элемента длины.

Согласно закону, установленному Ампером, на элемент тока d l действует в магнитном поле сила

d f = ki d l ´ B (46.1)

(k – коэффициент пропорциональности, i – сила тока, В – магнитная индукция в том месте, где помещается элемент d l).

Величина силы (46.1) вычисляется по формуле

d f = kiB d l sin a (46.2)

где a – угол между векторами d l и В (рис. 84,a). Направлена сила перпендикулярно к плоскости, в которой лежат векторы d l и В.

Правило левой руки.

Направление силы, действующей на ток, удобно определять с помощью так называемого правила левой руки. Если расположить левую руку так, чтобы вектор В «вонзался» в ладонь, а четыре сложенные вместе пальца были направлены вдоль тока, то отставленный в сторону большой палец укажет направление силы (рис. 84,6).

Проверим закон Ампера для дифференциалов при вычислении силы взаимодействия двух находящихся в вакууме параллельных бесконечно длинных прямых токов. Если расстояние между токами b (рис. 85), то каждый элемент тока i ₂ будет находиться в магнитном поле, индукция которого . Угол a между элементами тока i ₂ и вектором В ₁ прямой.

Дата добавления: 2015-04-24