Описание поля в диэлектриках. Вектор электрического смещения. Диэлектрическая проницаемость

Под напряженностью поля в диэлектрике понимают значение Е, получающееся усреднением истинного поля по физически бесконечно малому объему. Истинное (микроскопическое) поле в диэлектрике сильно меняется в пределах меж молекулярных расстояний. Однако при рассмотрении действия поля на макроскопические тела эти изменения сказываться не будут и действие поля на тело определяется усредненным (макроскопическим) значением Е.

Макроскопическое поле Е получается в результате наложения двух полей: поля Е ₀, создаваемого свободными зарядами, т. е. такими зарядами, которые могут передаваться от одного тела к другому при их касании, и поля Е ' связанных зарядов. В силу принципа суперпозиции полей

Е = Е ₀ + Е ' (16.1)

Поляризация диэлектрика обусловлена действием суммарного поля (16.1). Следовательно, именно это Е нужно подставлять в формулы (15.2) и (15.12).(P = ke ₀ E; s ’ = ke ₀ E _n)

Связанные заряды отличаются от свободных лишь тем, что не могут покинуть пределы молекулы (или атома), в состав которой они входят. В остальном же их свойства таковы, как и у всех прочих зарядов. В частности, на связанных -зарядах начинаются либо заканчиваются q '/ e ₀ линий вектора Е '. Поэтому теорему Гаусса для определяемого выражением (16.1) вектора Е нужно записывать следующим образом:

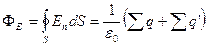(16.2)

т. е. при вычислении потока вектора Е через замкнутую поверхность следует учитывать алгебраическую сумму не только свободных, но также и связанных зарядов, заключенных внутри поверхности. Поэтому формула (16.2) оказывается малопригодной для нахождения вектора Е в диэлектрике – она выражает свойства неизвестной величины Е через связанные заряды q ', которые в свою очередь определяются неизвестной Е [см. формулу (15.12)].

К счастью, затруднение, обусловленное тем, что Е зависит также и от связанных зарядов, можно обойти, введя в рассмотрение вспомогательную величину, связанную простым соотношением с вектором Е и определяемую лишь распределением в пространстве свободных зарядов. Чтобы установить вид этой вспомогательной величины, сопоставим формулу (16.2) с выражением (15.9) (). С точностью до знака и множителя 1/ e ₀ правая часть выражения (15.9) совпадает со второй из сумм в формуле (16.2). Это дает возможность исключить из соотношений заряды q ', заменив их потоком вектора Р.

Легко проверить, что, объединив вместе (15.9) и (16.2), можно получить следующую формулу:

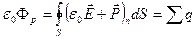(16.3)

Выражение, стоящее в скобках под знаком интеграла, и есть та вспомогательная величина, о которой шла речь выше. Ее обозначают буквой D и называют электрическим смещением (или электрической индукцией).

Итак, электрическим смещением (электрической индукцией) называется физическая величина, определяемая соотношением

D = e ₀ E + P. (16.4)

С использованием этой величины формула (16.3) может быть записана в виде

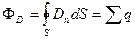(16.5)

Если свободные заряды распределены внутри замкнутой поверхности непрерывно с объемной плотностью r, формула (16.5) видоизменяется следующим образом:

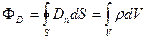(16.6)

Формулы (16.5) и (16.6) выражают теорему Гаусса для вектора электрического смещения: поток вектора электрического смещения через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных зарядов.

В вакууме Р = 0, так что определяемая выражением (16.4) величина D превращается в e ₀ E и формулы (16.5) и (16.6) переходят в формулы (8.3) и (8.4).

Единицей потока вектора электрического смещения является кулон (K). Согласно (16.5) заряд в 1 к создает через охватывающую его поверхность поток смещения в 1 K.

Подставив в формулу (16.4) выражение (15.2 P = ke ₀ E) для Р, получим

D = e ₀ Е + ke ₀ Е = e ₀ (1 + k) Е. (16.7)

Безразмерную величину

e = 1 + k (16.8)

называют относительной диэлектрической проницаемостью или. просто диэлектрической проницаемостью среды. Следовательно, соотношение (16.7) можно записать в виде

D = e ₀ e Е (16.9)

(В анизотропных диэлектриках направления D и Е, вообще говоря, не совпадают)

Это и есть то простое соотношение между векторами Е и D, о котором речь была выше. Согласно формулам (5.3) и (16.9) электрическое смещение поля точечного заряда в вакууме равно

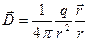(16.10)

Единицей электрического смещения служит кулон на квадратный метр (к/м²).

Чтобы выяснить физический смысл величин D и e, рассмотрим пример поля в диэлектрике.

Дата добавления: 2015-04-24