Диполь в однородном и неоднородном электрических полях

Если диполь поместить в однородное электрическое поле, образующие диполь заряды + q и – q окажутся под действием равных по величине, но противоположных по направлению сил f ₁ и f ₂ (рис.. 28). Эти силы образуют пару, плечо которой равно l sin a, т. е. зависит от ориентации диполя относительно поля. Модуль каждой из сил равен qE. Умножив его на плечо, получим величину момента пары сил, действующих на диполь:

М = qEl sina = pE sina, (14.1)

где р – электрический момент диполя.

Формула (14.1), очевидно, может быть написана в векторном виде

М = р ´ Е. (14.2)

Момент (14.2) стремится повернуть диполь так, чтобы его момент р установился по направлению поля.

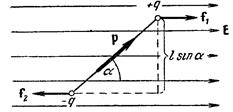Рис. 28

Чтобы увеличить угол между векторами р и Е на da, нужно совершить против сил, действующих на диполь в электрическом поле, работу

dA = Mda. = pE sin a d a.

Эта работа идет на увеличение потенциальной энергии W, которой обладает диполь в электрическом поле

dW = pEsin a d a. (14.3)

Интегрирование выражения (14.3) дает для энергии диполя в электрическом поле выражение

W = – pE cos a + const.

Наконец, полагая const равной нулю, получаем

W = – pE cos a = – pE. (14.4)

Выбрав таким образом значение const, мы полагаем энергию диполя равной нулю в том случае, когда диполь устанавливается перпендикулярно к полю. Наименьшее значение энергии, равное – рЕ, получается при ориентации диполя по направлению поля, наибольшее, равное рЕ, – при р, направленном в сторону, противоположную Е.

В неоднородном поле силы, действующие на заряды диполя, вообще говоря, не одинаковы по величине. При малых размерах диполя силы f ₁ и f ₂ можно приближенно считать коллинеарными (рис. 29). Предположим, что поле изменяется быстрее всего в направлении х,

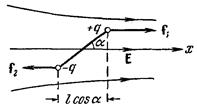рис. 29.

совпадающем с направлением Е в том месте, где расположен диполь. Положительный заряд диполя смещен относительно отрицательного в направлении х на величину D х = l cos a. Поэтому напряженность поля в точках, где помещаются заряды, отличается на 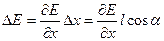. Следовательно, результирующая f ₁ + f ₂, действующая на диполь, будет отлична от нуля. Проекция этой результирующей на ось х, очевидно, равна

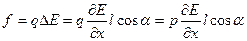(14.5)

Таким образом, в неоднородном поле на диполь, кроме вращательного момента A4.2), действует сила A4.5). Под действием этой силы диполь будет либо втягиваться в область более сильного поля (угол a острый), либо выталкиваться из нее (угол a тупой). Отметим, что выражение для силы f можно получить из формулы A4.4) для энергии диполя, использовав известное из механики соотношение между потенциальной энергией и силой. Действительно, продифференцировав A4.4) по х в предположении, что a (т. е. ориентация диполя) остается постоянной, и изменив у результата знак на обратный, мы придем к формуле A4.5).

Дата добавления: 2015-04-24