Взаимодействие токов. 3 страница

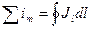D4.3)

Исключив из формул (44.2) и (44.3) сумму молекулярных токов, легко получить следующее соотношение:

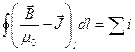(44.4)

Выражение, стоящее в скобках под знаком интеграла, и есть искомая вспомогательная величина. Ее обозначают буквой Н и называют напряженностью магнитного поля.

Итак, напряженностью магнитного поля называется физическая величина, определяемая соотношением

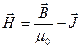(44.5)

С использованием этой величины формула (44.4) может быть записана в виде

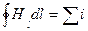(44.6)

Если макроскопические токи распределены в пространстве с плотностью j, формула (44.6) видоизменяется следующим образом:

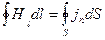(44.7)

(S – произвольная поверхность, ограниченная контуром, по которому берется циркуляция). Формулы (44.6) и (44.7) выражают теорему о циркуляции вектора Н: циркуляция вектора напряженности магнитного поля по некоторому контуру равна алгебраической сумме макроскопических токов, охватываемых этим контуром.

Из сказанного выше вытекает, что напряженность магнитного поля Н является аналогом электрического смещения (электрической индукции) D. Первоначально предполагалось, что в природе имеются подобные электрическим зарядам магнитные массы, и учение о магнетизме развивалось по аналогии с учением об электричестве. В те времена и были введены названия: «магнитная индукция» для В и «напряженность поля» для Н.

Впоследствии выяснилось, что магнитных масс в природе не существует и что величина, названная магнитной индукцией, в действительности является аналогом не электрического смещения D, а напряженности электрического поля Е (соответственно Н –– аналогом не Е, a D). Однако изменять уже установившуюся терминологию не стали, тем более, что вследствие различной природы электрического и магнитного полей (электростатическое поле потенциально, магнитное – соленоидально) величины В и D обнаруживают много сходства в своем поведении (например, линии В, как и линии D, не претерпевают разрыва на границе двух сред).

В вакууме J = 0, поэтому Н превращается в В / m ₀ и формулы (44.6) и (44.7) переходят в формулы (42.3 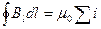) и (42.4 ).

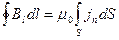Из (41.1 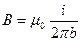) следует, что напряженность поля прямого тока в вакууме определяется выражением

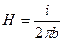(44.8)

из которого видно, что напряженность магнитного поля имеет размерность, равную размерности силы тока, деленной на размерность длины. В соответствии с этим единица напряженности магнитного поля в СИ носит название ампер на метр (а/м). Согласно (44.8) на расстоянии b = 1/2 p (м)от прямого провода, по которому течет ток силой 1 а, напряженность магнитного поля равна 1 а/м. В этом случае магнитная индукция равна 4p×10^–7 тл.

Вектор намагничения J принято связывать не с магнитной индукцией, а с напряженностью поля. Как показывает опыт, вектор J связан с вектором Н в той же точке магнетика соотношением

J = c H (44.12)

где c – характерная для данного магнетика величина, называемая магнитной восприимчивостью1). Согласно (44.5) размерность Н совпадает с размерностью J. Следовательно, c –безразмерная величина.

Подставив в формулу (44.5 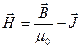) выражение (44.12) для J, получим

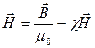
откуда

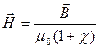(44.13)

Безразмерная величина

m =1+ c (44.14)

называется относительной магнитной проницаемостью или просто магнитной проницаемостью вещества.

В отличие от диэлектрической восприимчивости k, которая принимает лишь положительные значения (вектор поляризации Р в изотропном диэлектрике всегда направлен по полю Е), магнитная восприимчивость c бывает как положительной, так и отрицательной. Поэтому магнитная проницаемость m может быть как больше, так и меньше единицы.

Подставив (44.14) в формулу (44.13), придем к соотношению

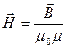(44.15)

которое и является тем простым соотношением между векторами В и Н, о котором упоминалось выше.

Таким образом, напряженность магнитного поля Н есть вектор, имеющий то же направление, что и вектор В, но в m ₀ m раз меньший по модулю (в анизотропных средах векторы Н и В могут не совпадать по направлению).

Перейдем к выяснению физического смысла величин Н и m. Рассмотрим однородное магнитное поле в вакууме, которое можно задать с помощью либо вектора В ₀, либо вектора H ₀ = В ₀/ m ₀. Вектор H ₀ мы назовем напряженностью внешнего поля. Внесем в это поле бесконечно длинный круглый стержень из однородного магнетика и расположим его вдоль В ₀

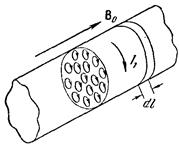Рис. 78.

(рис. 78). Под действием поля молекулярные токи установятся так, что их магнитные моменты расположатся вдоль оси стержня, вследствие чего их плоскости станут перпендикулярными к этой оси. Рассмотрим молекулярные токи, лежащие в произвольно выбранном поперечном сечении стержня. В каждой точке внутри стержня смежные молекулярные токи текут в противоположные стороны, так что их совместное действие равно нулю. Некомпенсированными будут лишь участки токов, примыкающие к поверхности стрежня. Таким образом, суммарное действие молекулярных токов будет таким, какое вызвал бы макроскопический ток, текущий по поверхности стержня. Обозначим силу этого тока, приходящуюся на единицу длины стержня (линейную плотность тока), через I ₁. Очевидно, что цилиндр, обтекаемый током, эквивалентен соленоиду с числом ампер–витков ni, равным линейной плотности тока I ₁. Следовательно, все молекулярные токи возбуждают совместно такое поле, какое создал бы в вакууме соленоид с числом ампер–витков, равным I ₁. Согласно формуле (42.6) магнитная индукция этого поля равна

В ' = m ₀ I ₁. (44.20)

Легко видеть, что направление В ' совпадает с направлением В ₀. Вне стержня В ' равна нулю.

Выделим мысленно в стержне перпендикулярный к оси слой толщины d l. Молекулярные токи, заключенные в объеме этого слоя, эквивалентны круговому току силы I ₁d l. Согласно формуле (39.1) магнитный момент этого тока равен

d p _m = I ₁ S d l

где S – площадь поперечного сечения стержня. Разделив d p _m на объем слоя d V = S d l, получим для намагничения стержня следующее выражение:

J = I ₁ (44.21)

Таким образом, намагничение стержня совпадает с линейной плотностью тока.

С учетом (44.21) формула (44.20) принимает вид

В ' = m ₀ J (44.22)

(мы воспользовались тем, что векторы В ' и J параллельны).

Складывая векторы В ' и В ₀, находим вектор магнитной индукции результирующего поля

B = В ₀ + В ' = В ₀ + m ₀ J

Наконец, подставив это значение В в формулу (44.5 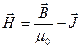), получаем

Н = B ₀/ m ₀ = Н ₀. (44.23)

Итак, в рассмотренном нами случае напряженность поля в магнетике совпадает с вектором магнитной индукции внешнего поля, деленным на m ₀, т. е. оказывается равной напряженности внешнего поля.

Согласно формуле (44.15 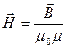), умножив Н на m ₀ m, мы получим индукцию В:

B = m ₀ m H = m ₀ m (B ₀/ m ₀) = m B ₀ (44.24)

Отсюда следует, что относительная магнитная проницаемость m показывает, во сколько раз усиливается поле в магнетике.

Заметим, что поскольку поле В ' отлично от нуля только внутри стержня, магнитное поле вне стержня остается без изменений.

Преломление линий магнитной индукции.

Выясним, что происходит на границе двух однородных изотропных магнетиков с разными m. Рассмотрим воображаемый цилиндр высоты h, основания которого S ₁ и S ₂ расположены по разные стороны поверхности раздела (рис. 79). Применим к этому цилиндру теорему Гаусса (44.1). Потоком В через боковую поверхность цилиндра можно пренебречь, так как h мы будем стремить к нулю. Поток через верхнее основание цилиндра равен B _1n S ₁, где B _1n – нормальная составляющая вектора В в первом магнетике в непосредственной близости к поверхности раздела. Аналогично поток через нижнее основание есть B _2n S ₂, где B _2n – нормальная составляющая вектора В во втором магнетике также в непосредственной близости

Рис. 79.

Рис. 80.

к поверхности раздела магнетиков.

Сложив эти два потока, мы получим полный поток, который согласно теореме Гаусса должен быть равен нулю:

Ф _B = B _1n S ₁ + B _2n S ₂ = (B _1n + B _2n) S = 0.

Отсюда следует, что B _1n = – B _2n. Если проектировать B ₁ и В ₂ на одну и ту же нормаль, то получится, что

B _1n = B _2n. (45.1)

Заменив согласно (44.15) составляющие В соответствующими составляющими вектора Н, умноженными на m ₀ m, получим соотношение

m ₀ m ₁ H _1n = H _2n m ₀ m ₂

из которого следует, что

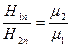(45.2)

Теперь возьмем на границе магнетиков прямоугольный контур (рис. 80) и вычислим для него циркуляцию Н. Ширину контура а возьмем столь малой, чтобы вкладом, вносимым в циркуляцию сторонами, перпендикулярными к поверхности раздела, можно было пренебречь. Тогда для циркуляции получается выражение b { Н _1t – Н _2t). Поскольку контур не охватывает макроскопических токов, циркуляция должна быть равна нулю [см. (44.6)], откуда вытекает, что

Н _1t = Н _2t (45.3)

Заменив согласно (44.15) составляющие Н соответствующими составляющими вектора В, деленными на m ₀ m, получим соотношение

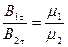(45.4)

Резюмируя, можно сказать, что при переходе через границу раздела двух магнетиков нормальная составляющая вектора В и тангенциальная составляющая вектора Н изменяются

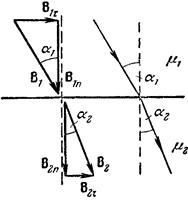Рис. 81.

непрерывно. Тангенциальная же составляющая вектора В и нормальная составляющая вектора Н при переходе через границу раздела претерпевают разрыв.

Таким образом, при переходе через границу раздела двух сред вектор В ведет себя аналогично вектору D, а вектор Н – аналогично вектору Е.

На рис. 81 показано поведение линий В при пересечении границы двух магнетиков. Обозначим углы между линиями В и нормалью к поверхности раздела соответственно a ₁ и a ₂. Отношение тангенсов этих углов равно

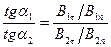
откуда с учетом (45.1) и (45.4) получается закон преломления линий магнитной индукции:

(45.5)

При переходе в магнетик с большей m линии магнитной индукции отклоняются от нормали к поверхности.

Легко видеть, что это приводит к сгущению линий. Сгущение линий В в веществе с большой магнитной проницаемостью дает возможность формировать магнитные

пучки, т. е. придавать им необходимую форму и направление. В частности, чтобы осуществить магнитную защиту некоторого объема, его окружают железным экраном. Как

Рис. 82.

Рис. 83.

видно из рис. 82, сгущение линий магнитной индукции в толще экрана приводит к ослаблению поля внутри.

На рис. 83 дана схема лабораторного электромагнита. Он состоит из железного ярма, на которое насажены питаемые током катушки. Линии магнитной индукции оказываются сосредоточенными в основном внутри ярма.

Лишь в узком воздушном зазоре они проходят в среде с малой m. Вектор В пересекает границы между воздушным зазором и ярмом по нормали к поверхности раздела. Отсюда согласно D5.1) следует, что магнитная индукция в зазоре и в ярме одинакова по величине. Применим теорему о циркуляции Н к контуру, проходящему по оси ярма. Напряженность поля с большой точностью можно считать всюду в железе одинаковой и равной H _жел = В / m ₀ m _жел. В воздухе H _возд = В / m ₀ m _возд.

Обозначим длину участка контура в железе через l _жел. а в зазоре– через l _возд. Тогда циркуляцию можно представить в виде H _жел l _жел + H _возд l _возд. Согласно (44.6) эта циркуляция должна быть равна Ni, где N – суммарное число витков катушек электромагнита, i – сила тока. Таким образом, имеем

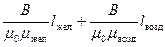
откуда

(m _возд отличается от единицы лишь в пятом знаке после запятой). Обычно l _возд бывает порядка 10 см = 0,1 м, l _жел – порядка 1 м, m _жел достигает значений порядка нескольких тысяч. Поэтому вторым слагаемым в знаменателе можно пренебречь и написать, что

(45.6)

Следовательно, магнитная индукция в зазоре электромагнита имеет такую величину, какую она имела бы внутри соленоида без сердечника, на единицу длины которого было бы намотано число витков, равное N / l _возд [см. (42.10) В = m ₀ ni ]. Увеличивая общее число витков и уменьшая размеры воздушного зазора, можно получать поля с большим значением В. С помощью электромагнитов с железным сердечником удается получать поля с В до ~1 Тл.

Классификация магнетиков.

Прежде чем изложить классификацию магнетиков, рассмотрим величины, с помощью которых принято характеризовать магнитные свойства разных веществ. В § 44 была введена для этой цели восприимчивость c, определяющая величину намагничения единицы объема вещества [см. формулу (44.12)].

Часто вместо восприимчивости единицы объема c пользуются отнесенной к одному киломолю вещества киломолярной (для химически простых веществ – килоатомной) восприимчивостью c _км (c _кат) или отнесенной к единице массы удельной восприимчивостью c _уд. Между значениями этих восприимчивостей имеются соотношения: c _км = cV _км где V _км – объем киломоля вещества (в м³/кмоль), c _уд = (1/ d) c, где d – плотность вещества (в кг/м³). В то время как c – безразмерная величина, c _км (или c _кат) имеет размерность м³/кмоль (или м³/кат), а c _уд – м³/кг.

Восприимчивость, отнесенная к молю (грамм-молекуле) вещества, называется молярной (для химически простых веществ – атомной). Очевидно, что c _м = cV _м, где V _м – объем моля вещества (в см³/моль).

В зависимости от знака и величины магнитной восприимчивости все магнетики подразделяются на три группы:

1) диамагнетики, у которых c отрицательна и мала (c _км ~ 10^–8 – 10^–7 м³/кмоль);

2) парамагнетики, у которых c невелика, но положительна (c _км ~ 10^–7 – 10^–6 м³/кмоль);

3) ферромагнетики, у которых c положительна и достигает очень больших значений (c _км ~ 10³ м³/кмоль).

Кроме того, в отличие от диа- и парамагнетиков, для которых c постоянна, магнитная восприимчивость ферромагнетиков является функцией напряженности магнитного поля. Таким образом, вектор намагничения J может как совпадать по направлению с Н (у пара- и ферромагнетиков), так и быть направленным в противоположную сторону (у диамагнетиков). Напомним, что у диэлектриков вектор поляризации всегда направлен в ту же сторону, что и Е.

Магнитомеханические явления.

Магнитные моменты атомов и молекул

В главе VII мы видели, что гипотеза Ампера о молекулярных токах позволяет объяснить многие явления в магнетиках. Природа молекулярных токов стала понятной после того, как опытами Резерфорда было установлено, что атомы всех веществ состоят из положительно заряженного ядра и движущихся вокруг него отрицательно заряженных электронов.

Согласно теории, развитой в 1913 г. Нильсом Бором, электроны в атомах движутся по круговым орбитам. Через площадку, расположенную в любом месте на пути электрона (рис. 94), переносится в единицу времени заряд ev, где е – заряд электрона, a v – число оборотов в

Рис. 94.

секунду. Следовательно, движущийся по орбите электрон образует круговой ток силы' i = ev. Поскольку заряд электрона отрицателен, направление движения электрона и направление тока противоположны. Магнитный момент создаваемого электроном тока равен

р _m = iS = evpr ²,

где r – радиус орбиты. Произведение 2 pr дает скорость движения электрона v, поэтому можно написать, что

р _m = evr /2 (51.1)

Момент (51.1), обусловлен движением электрона по орбите, вследствие чего называется орбитальным магнитным моментом электрона. Направление вектора р _m образует с направлением тока правовинтовую, а с направлением движения электрона левовинтовую систему (рис. 94).

Движущийся по орбите электрон обладает моментом импульса

L = mvr (51.2)

(m – масса электрона). Вектор L называют орбитальным механическим моментом электрона. Он образует с направлением движения электрона правовинтовую систему. Следовательно, направления векторов р _m и L противоположны.

Отношение магнитного момента элементарной частицы к ее механическому моменту называется гиромагнитным отношением. Для электрона оно равно

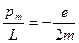(51.3)

(знак «–» указывает на то, что направления моментов противоположны).

Вследствие вращения вокруг ядра электрон оказывается подобным волчку. Это обстоятельство лежит в основе так называемых гиромагнитных или магнитомеханических явлений, заключающихся в том, что намагничение магнетика приводит к его вращению и, наоборот, вращение магнетика вызывает его намагничение. Существование первого явления было доказано экспериментально Эйнштейном и де Хаасом, второго – Барнеттом.

В основе опыта Эйнштейна и де Хааса лежат следующие соображения. Если намагнитить стержень из магнетика, то орбитальные магнитные моменты электронов установятся по направлению поля, а механические моменты – против поля. В результате суммарный механический момент электронов S L _i станет отличным от нуля (первоначально вследствие хаотической ориентации отдельных моментов он был равен нулю). Момент импульса системы

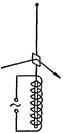Рис. 95.

стержень + электроны должен остаться без изменений. Поэтому стержень приобретает момент импульса, равный – 2jL/, т. е. придет во вращение. Изменение направления намагничения приведет к изменению направления вращения стержня.

Механическую модель этого опыта можно осуществить, поставив человека на вращающийся стул и дав ему в руки вращающееся велосипедное колесо. Поворачивая колесо вверх, человек приходит во вращение в сторону, противоположную направлению вращения колеса. Поворачивая колесо вниз, человек приходит во вращение в противоположную сторону.

Опыт Эйнштейна и де Хааса осуществлялся следующим образом (рис. 95). Тонкий железный стержень подвешивался на упругой закручивающейся нити и помещался внутрь соленоида. Закручивание нити при намагничении стержня постоянным магнитным полем получалось весьма малым. Для усиления эффекта был применен метод резонанса – соленоид питался переменным током, частота которого подбиралась равной собственной частоте механических колебаний системы. При этих условиях амплитуда колебаний достигала значений, которые можно было измерить, наблюдая смещения светового зайчика, отраженного от зеркальца, укрепленного на нити. Из данных опыта было вычислено гиромагнитное отношение, которое получилось равным – e / m. Таким образом, знак заряда носителей, создающих молекулярные токи, совпал со знаком заряда электрона. Однако полученный результат превысил ожидаемое значение гиромагнитного отношения (51.3) в два раза.

Чтобы понять опыт Барнетта, вспомним, что при попытках вовлечь гироскоп во вращение вокруг некоторого направления ось гироскопа поворачивается так, чтобы направления собственного и принудительного вращений гироскопа совпали. Если установить гироскоп, закрепленный в карданном подвесе, на диск центробежной машины и привести ее во вращение, то ось гироскопа установится по вертикали, причем так, что направление вращения гироскопа совпадет с направлением вращения диска. При изменении направления вращения центробежной машины ось гироскопа поворачивается на 180°, т. е. так, чтобы направления обоих вращений снова совпали.

Барнетт приводил железный стержень в очень быстрое вращение вокруг его оси и измерял возникающее при этом намагничение. Из результатов этого опыта Барнетт также получил для гиромагнитного отношения величину, в два раза превышающую значение (51.3).

В дальнейшем выяснилось, что кроме орбитальных моментов (51.1) и (51.2) электрон обладает собственным механическим L _s и магнитным p _ms моментами, для которых гиромагнитное отношение равно

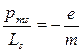
т. е. совпадает со значением, полученным в опытах Эйнштейна и де Хааса и Барнетта. Отсюда следует, что магнитные свойства железа обусловлены не орбитальным, а собственным магнитным моментом электронов.

Существование собственных моментов электрона первоначально пытались объяснить, рассматривая электрон как заряженный шарик, вращающийся вокруг своей оси.

В соответствии с этим собственный механический момент электрона получил название спин (от английского to spin – вращаться). Однако вскоре обнаружилось, что такое представление приводит к ряду противоречий, и от гипотезы о «вращающемся» электроне пришлось отказаться. В настоящее время принимается, что собственный механический момент (спин) и связанный с ним собственный (спиновый) магнитный момент являются такими же неотъемлемыми свойствами электрона, как его масса и заряд.

Спином обладают не только электроны, но и другие элементарные частицы.

Спин элементарных частиц оказывается целым или полуцелым кратным величины ħ, которая равна постоянной Планка h, деленной на 2 p:

ħ = h /2 p = 1,05×10^–34 дж×сек (51.5)

В частности, для электрона L _s = ½ ħ, в связи с чем говорят, что спин электрона равен ½. Таким образом, ħ представляет собой как бы естественную единицу момента импульса, подобно тому как элементарный заряд е является естественной единицей заряда.

В соответствии с (51.4) собственный магнитный момент электрона равен

p _ms = –(e/m) L _s = –(e/m)(ħ /2) = –(eħ /2 m) (51.6)

Величину

m _в = –(eħ /2 m) = 0,92710^–23 джоуль/тесла (51.7)

называют магнетоном Бора. Следовательно, собственный магнитный момент электрона равен одному магнетону Бора.

Магнитный момент атома слагается из орбитальных и собственных моментов входящих в его состав электронов, а также из магнитного момента ядра (который обусловлен магнитными моментами входящих в состав ядра элементарных частиц:–протонов и нейтронов).

Магнитный момент ядра значительно меньше моментов электронов, поэтому при рассмотрении многих вопросов им можно пренебречь и считать, что магнитный момент атома равен векторной сумме магнитных моментов электронов. Магнитный момент молекулы также можно считать равным сумме магнитных иомеатов входящих в ее состав электронов.

Экспериментальное определение магнитных моментов атомов и молекул было осуществлено Штерном и Герлахом. В их опытах молекулярный лучок пропускался через магнитное поле с большим градиентом. Неоднородность доля достигалась за счет специальной формы полюсных наконечников электромагнита (рис. 96). Согласно формуле (48.8) на атомы

Дата добавления: 2015-04-24