Общий случай 4 страница

Модуль силы Лоренца (см. (114.1)) равен F=QvB sina, где a — угол между v и В.

Отметим еще раз (см. § 109), что маг­нитное поле не действует на покоящийся электрический заряд. В этом существенное отличие магнитного поля от электрическо­го. Магнитное поле действует только на движущиеся в нем заряды. Сила Лоренца всегда перпендикуляр­на скорости движения заряженной части­цы, поэтому она изменяет только направ­ление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает. Иными словами, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изме­няется.

Если на движущийся электрический заряд помимо магнитного поля с индук­цией В действует и электрическое поле с напряженностью Е, то результирующая сила F, приложенная к заряду, равна век­торной сумме сил — силы, действующей со стороны электрического поля, и силы Ло­ренца:

F = Q E + Q [ vB ].

Это выражение называется формулой Ло­ренца. Скорость v в этой формуле есть скорость заряда относительно магнитного поля.

Движение заряженных частиц в магнитном поле

Выражение для силы Лоренца (114.1) по­зволяет найти ряд закономерностей дви­жения заряженных частиц в магнитном поле. Направление силы Лоренца и на­правление вызываемого ею отклонения за­ряженной частицы в магнитном поле за­висят от знака заряда Q частицы. На этом основано определение знака заряда частиц, движущихся в магнитных полях.

Для вывода общих закономерностей будем считать, что магнитное поле одно­родно и на частицы электрические поля не действуют. Если заряженная частица дви­жется в магнитном поле со скоростью v вдоль линий магнитной индукции, то угол а между векторами v и В ра­вен 0 или p. Тогда по формуле (114.1) сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она дви­жется равномерно и прямолинейно.

Если заряженная частица движется в магнитном поле со скоростью v, перпен­дикулярной вектору В, то сила Лоренца F =Q[ vB ] постоянна по модулю и нор­мальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центростремительное ускорение. Отсюда следует, что частица будет двигаться по окружности, радиус r которой определяет­ся из условия

QvB = mv²/r, откуда

Период вращения частицы, т. е. вре­мя Т, затрачиваемое ею на один полный оборот,

T = 2nr/v. Подставив сюда выражение (115.1), по­лучим т. е. период вращения частицы в однород­ном магнитном поле определяется только величиной, обратной удельному заряду (Q/m) частицы, и магнитной индукцией поля, но не зависит от ее скорости (при v << с)). На этом основано действие цикли­ческих ускорителей заряженных частиц (см. §116).

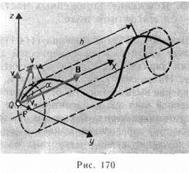
Если скорость v заряженной частицы направлена под углом а к вектору В (рис. 170), то ее движение можно пред­ставить в виде суперпозиции: 1) равно­мерного прямолинейного движения вдоль поля со скоростью v_||=vcosa; 2) равно­мерного движения со скоростью v _┴= v sina по окружности в плоскости, пер­пендикулярной полю. Радиус окружности определяется формулой (115.1) (в данном случае надо заменить v на v_┴=vsina). В результате сложения обоих движений возникает движение по спирали, ось кото­рой параллельна магнитному полю (рис. 170). Шаг винтовой линии h=v _|| T=vT cosa. Подставив в последнее выражение (115.2), получим h=2pmv cosa/(BQ) Направление, в котором закручивается спираль, зависит от знака заряда ча­стицы. Если скорость v заряженной частицы составляет угол а с направлением векто­ра В неоднородного магнитного поля, ин­дукция которого возрастает в направле­нии движения частицы, то r и h уменьша­ются с ростом В. На этом основана фокусировка заряженных частиц в маг­нитном поле.

Эффект Холла

Эффект Холла (1879) — это возникнове­ние в металле (или полупроводнике) с то­ком плотностью j, помещенном в магнит­ное поле В, электрического поля в направ­лении, перпендикулярном В и j.

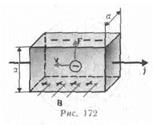
Поместим металлическую пластинку с током плотностью j в магнитное поле В, перпендикулярное j (рис.172). При дан­ном направлении j скорость носителей тока в металле — электронов — направ­лена справа налево. Электроны испытыва­ют действие силы Лоренца (см. §114), которая в данном случае направлена вверх. Таким образом, у верхнего края пластинки возникнет повышенная концен­трация электронов (он зарядится отрица­тельно), а у нижнего — их недостаток (за­рядится положительно). В результате это­го между краями пластинки возникнет дополнительное поперечное электрическое поле, направленное снизу вверх. Когда напряженность Е_B этого поперечного поля достигнет такой величины, что его дейст­вие на заряды будет уравновешивать силу Лоренца, то установится стационарное распределение зарядов в поперечном на­правлении. Тогда еЕ_B=еDj /а = еvВ, или Dj=vВа, где а — ширина пластинки, Dj — попереч­ная (холловская) разность потенциалов.

Учитывая, что сила тока I =jS=nevS (S — площадь поперечного сечения пластинки толщиной d, n — концентрация электронов, v — средняя скорость упоря­доченного движения электронов), получим

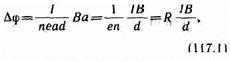т. е. холловская поперечная разность по­тенциалов прямо пропорциональна маг­нитной индукции В, силе тока I и обратно пропорциональна толщине пластинки d. В формуле (117.1) R= 1 /(en) — постоян­ная Холла, зависящая от вещества. По измеренному значению постоянной Холла можно: 1) определить концентрацию носи­телей тока в проводнике (при известных характере проводимости и заряде носите­лей); 2) судить о природе проводимости полупроводников (см. §242, 243), так как знак постоянной Холла совпадает со зна­ком заряда е носителей тока. Эффект Хол­ла поэтому наиболее эффективный метод изучения энергетического спектра носите­лей тока в металлах и полупроводниках. Он применяется также для умножения постоянных токов в аналоговых вычисли­тельных машинах, в измерительной техни­ке (датчики Холла) и т. д.

Циркуляция вектора В для магнитного поля в вакууме

Аналогично циркуляции вектора напря­женности электростатического поля (см. § 83) введем циркуляцию вектора магнитной индукции. Циркуляцией векто­ра В по заданному замкнутому контуру называется интеграл 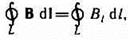где d l — вектор элементарной длины кон­тура, направленной вдоль обхода контура, В ₁= В cosa — составляющая вектора В в направлении касательной к контуру (с учетом выбранного направления обхо­да), а — угол между векторами В и d l.

Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В): циркуляция вектора В по про­извольному замкнутому контуру равна произведению магнитной постоянной m₀ на алгебраическую сумму токов, охватывае­мых этим контуром:

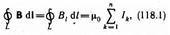
где n — число проводников с токами, ох­ватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается конту­ром. Положительным считается ток, на­правление которого связано с направлени­ем обхода по контуру правилом правого винта; ток противоположного направления считается отрицательным. Например, для системы токов, изображенных на рис. 173,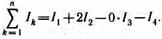

Выражение (118.1) справедливо толь­ко для поля в вакууме, поскольку, как будет показано ниже, для поля в веществе необходимо учитывать молекулярные токи.

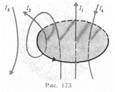Продемонстрируем справедливость теоремы о циркуляции вектора В на примере магнитного поля прямого тока I, пер­пендикулярного плоскости чертежа и на­правленного к нам (рис. 174). Представим себе замкнутый контур в виде окружности радиуса r. В каждой точке этого контура вектор В одинаков по модулю и направлен по касательной к окружности (она являет­ся и линией магнитной индукции). Следо­вательно, циркуляция вектора В равна

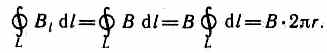Согласно выражению (118.1), получим В •2p r =m₀ I (в вакууме), откуда B =m₀/(2pr). Таким образом, исходя из теоремы о цир­куляции вектора В получили выражение для магнитной индукции поля прямого тока, выведенное выше (см. (110.5)). Сравнивая выражения (83.3) и (118.1) для циркуляции векторов Е и В, видим, что между ними существует при­нципиальное различие. Циркуляция векто­ра Е электростатического поля всегда рав­на нулю, т. е. электростатическое поле яв­ляется потенциальным. Циркуляция век­тора В магнитного поля не равна нулю. Такое поле называется вихревым. Теорема о циркуляции вектора В имеет в учении о магнитном поле такое же значе­ние, как теорема Гаусса в электростатике, так как позволяет находить магнитную индукцию поля без применения закона Био — Савара — Лапласа.

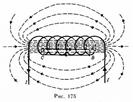Магнитное поле соленоида и тороида

Рассчитаем, применяя теорему о циркуля­ции, индукцию магнитного поля внутри соленоида. Рассмотрим соленоид длиной l, имеющий N витков, по которому течет ток (рис. 175). Длину соленоида считаем во много раз больше, чем диаметр его витков, т. е. рассматриваемый соленоид бесконечно длинный. Экспериментальное изучение маг­нитного поля соленоида (см. рис. 162, б) показывает, что внутри соленоида поле является однородным, вне соленоида — неоднородным и очень слабым.

Для нахождения магнитной индукции В выберем замкнутый прямоугольный кон­тур ABCDA, как показано на рис.175. Циркуляция вектора В по замкнутому кон­туру ABCDA, охватывающему все N вит­ков, согласно (118.1), равна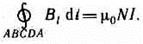

Интеграл по ABCDA можно представить в виде четырех интегралов: по АВ, ВС, CD и DA. На участках АВ и CD контур перпендикулярен линиям магнитной ин­дукции и В ₁=0. На участке вне соленоида В =0. На участке DA циркуляция векто­ра В равна Вl (контур совпадает с линией магнитной индукции); следовательно, 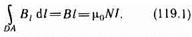да (в вакууме): B=m₀NI/l. (119.2)

Получили, что поле внутри соленоида од­нородно (краевыми эффектами в об­ластях, прилегающих к торцам соленоида, при расчетах пренебрегают). Важное значение для практики имеет также магнитное поле тороида —кольце­вой катушки, витки которой намотаны на сердечник, имеющий форму тора (рис. 176). Магнитное поле, как показыва­ет опыт, сосредоточено внутри тороида, вне его поле отсутствует.

Линии магнитной индукции в данном случае, как следует из соображений сим­метрии, есть окружности, центры которых расположены по оси тороида. В качестве контура выберем одну такую окружность радиуса r. Тогда, по теореме о циркуля­ции (118.1), B • 2pr=m ₀ NI, откуда следует, что магнитная индукция внутри тороида (в вакууме) В =m₀ NI/ (2p r), где N — число витков тороида.

Если контур проходит вне тороида, то токов он не охватывает и В • 2pr= 0. Это означает, что поле вне тороида отсутству­ет (что показывает и опыт).

Поток вектора магнитной индукции. Теорема Гаусса для поля В

Потоком вектора магнитной индукции (магнитным потоком) через площадку d S называется скалярная физическая величи­на, равная dФ_B= B d S =B_n dS,(120.1)где B_n=В cosa — проекция вектора В на направление нормали к площадке dS (a — угол между векторами n и В), d S =dS n — вектор, модуль которого ра­вен dS, а направление совпадает с направ­лением нормали n к площадке. Поток век­тора В может быть как положительным, так и отрицательным в зависимости от знака cosa (определяется выбором поло­жительного направления нормали n). Обычно поток вектора В связывают с оп­ределенным контуром, по которому течет ток. В таком случае положительное на­правление нормали к контуру нами уже определено (см. §109): оно связывается с током правилом правого винта. Таким образом, магнитный поток, создаваемый контуром через поверхность, ограничен­ную им самим, всегда положителен. Поток вектора магнитной индук­ции Ф_B через произвольную поверхность S равен 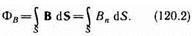Для однородного поля и плоской по­верхности, расположенной перпендикуляр­но вектору В, B _n= B =const и Ф_В=ВS.

Из этой формулы определяется единица магнитного потока вебер (Вб): 1 Вб — магнитный поток, проходящий через плоскую поверхность площадью 1 м², рас­положенную перпендикулярно однородно­му магнитному полю, индукция которого равна 1 Тл (1 Вб=1 Тл•м²).

Теорема Гаусса для поля В: поток век­тора магнитной индукции через любую замкнутую поверхность равен нулю: 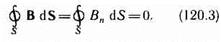Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми. Итак, для потоков векторов В и Е сквозь замкнутую поверхность в вихревом и потенциальном полях получаются раз­личные выражения (см. (120.3), (81.2)). В качестве примера рассчитаем поток вектора В через соленоид. Магнитная ин­дукция однородного поля внутри соленои­да с сердечником с магнитной проницае­мостью (г, согласно (119.2), равна В=m₀m,NI/l.

Магнитный поток через один виток со­леноида площадью S равен Ф₁=ВS, а полный магнитный поток, сцепленный со всеми витками соленоида и называемый потокосцеплением,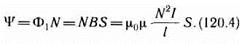

Работа по перемещению проводника и контура с током в магнитном поле

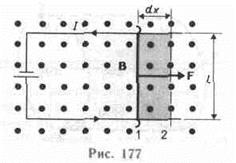На проводник с током в магнитном поле действуют силы, определяемые законом Ампера (см. §111). Если проводник не закреплен (например, одна из сторон кон­тура изготовлена в виде подвижной пере­мычки, рис. 177), то под действием силы Ампера он будет в магнитном поле переме­щаться. Следовательно, магнитное поле совершает работу по перемещению про­водника с током.

Для определения этой работы рассмотрим проводник длиной l с током I (он может свободно перемещаться), помещен­ный в однородное внешнее магнитное по­ле, перпендикулярное плоскости контура. При указанных на рис. 177 направлениях тока и поля сила, направление которой определяется по правилу левой руки, а значение — по закону Ампера (см. (111.2)), равна

F=IBl.

Под действием этой силы проводник пере­местится параллельно самому себе на от­резок Ах из положения 1 в положение 2. Работа, совершаемая магнитным полем, равна

dA=Fdx=IBldx =IB dS= I dФ, так как l dx=dS— площадь, пересекае­мая проводником при его перемещении в магнитном поле, В dS=dФ — поток век­тора магнитной индукции, пронизываю­щий эту площадь. Таким образом,

d A = I dФ, (121.1) Проинтегрировав выражение (121.1), оп­ределим работу, совершаемую силами Ам­пера, при конечном произвольном переме­щении контура в магнитном поле:

A = I DФ, (121.6) т. е. работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на из­менение магнитного потока, сцепленного

с контуром. Формула (121.6) остается справедливой для контура любой формы в произвольном магнитном поле.

Основы термодинамики. Число степеней свободы молекулы. Закон Больомана о равномерном распределении энергии по степеням свободы молекул. Первое начало термодинамики применительно к изопроцессам (изотермический, изохорный, адиабатный, изобарный). Работа, теплоемкость (удельная, молярная) Графики процессов на р-v диаграмме. Круговые процессы (циклы). Обратимые и необратимые процессы. Энтропия. Второе начало термодинамики. Тепловые двигатели и холодильные машины. Цикл Карно. Третье начало термодинамики
Реальный газ. Уравнение реального газа.

Важной характеристикой термодинамической системы является ее внутренняя энергия –энергия хаотического теплового движения микрочастиц системы(молекул, атомов, электронов, ядер и т.д.) и энергия взаимодействия этих частиц.

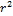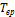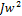Число степеней свободы: это число независимых переменных (координат), полностью определяющих положение системы в пространстве. В ряде задач молекулу одноатомного газа рассматривают как материальную точку, которой приписывают три степени свободы поступательного движения. При этом вращательное движение можно не учитывать (r→0, J=m →0, = /2→0)

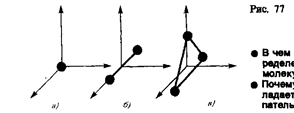
В классической механике молекула двухатомного газа в первом приближении рассматривается как совокупность двух материальных точек, жестко связанных неде­формируемой связью (рис. 77, б). Эта система кроме трех степеней свободы поступа­тельного движения имеет еще две степени свободы вращательного движения. Вращение вокруг третьей оси (оси, проходящей через оба атома) лишено смысла. Таким образом, двухатомный газ обладает пятью степенями свободы (i = 5). Трехатомная (рис. 77, я) и многоатомная нелинейные молекулы имеют шесть степеней свободы: три поступательных и три вращательных.

Независимо от общего числа степеней свободы молекул три степени свободы всегда поступательные. Ни одна из поступательных степеней свободы не имеет преиму­щества перед другими, поэтому на каждую из них приходится в среднем одинаковая энергия, равная 1/3 значения <  ₀> в (43.8):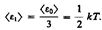

В классической статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/ 2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень «обладает» вдвое большей энергией потому, что на нее прихо­дится не только кинетическая энергия (как в случае поступательного и вращательного движений), но и потенциальная, причем средние значения кинетической и потенциаль­ной энергий одинаковы. Таким образом, средняя энергия молекулы 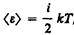где i — сумма числа поступательных, числа вращательных в удвоенного числа колеба­тельных степеней свободы молекулы: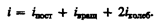

Так как в идеальном газе взаимная потенциальная энергия молекул равна нулю (молекулы между собой не взаимодействуют), то внутренняя энергия, отнесенная к одному молю газа, будет равнасумме кинетических энергий N _a молекул: 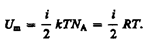Внутренняя энергия для произвольной массы т газа. 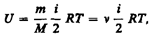где М — молярная масса,  — количество вещества.

Дата добавления: 2015-04-24