Применение первого начала термодинамики

Среди равновесных процессов, происходящих с термодинамическими системами, выде­ляются изопроцессы, при которых один из основных параметров состояния сохраняется постоянным.

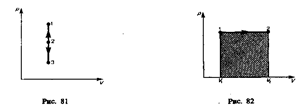
Изохорный процесс (V =const). Диаграмма этого процесса (изохора) в координатах р, V изображается прямой, параллельной оси ординат (рис. 81), где процесс 1—2 есть изохорное нагревание, а 1 — 3 — изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е. из первого начала термодинамики (Q= d U+A)дляизохорного процесса следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии: Тогда для произвольной массы газа получим

Изобарный процесс (p =const). Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, параллельной оси V. При изобарном процессе работа газа (см. (52.2)) при увеличения объема от V ₁ до V ₂ равна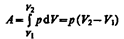

и определяется площадью заштрихованного прямоугольника (рис. 82). Если испо­льзовать уравнение Клапейрона — Менделеева для выбранных нами двух состояний, то 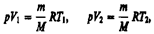откуда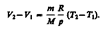

Тогда выражение для работы изобарного расширения примет вид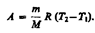

Из этого выражения вытекает физический смысл молярной газовой постоянной R:если T ₂ — T ₁ =1 К, то для 1 моль газа R=A, т. е. R численно равна работе изобарного расширения 1 моль идеального газа при нагревании его на 1 К.

В изобарном процессе при сообщении газу массой т количества теплоты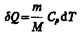

его внутренняя энергия возрастает на величину

Изотермический процесс (T =const). Как уже указывалось, изотермический процесс описывается законом Бойля—Мариотта: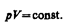

Диаграмма этого процесса (изотерма) в координатах р, V представляет собой гиперболу расположенную на диаграмме тем выше, чем выше температура, при которой происходит процесс.

найдем работу изотермического расширения газа:

Так как при Т =const внутренняя энергия идеального газа не изменяется: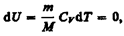

то из первого начала термодинамики (Q= d U+A) следует, что для изотермического процесс т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил: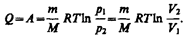

Адиабатическим называется процесс, при котором отсутствует теплообмен (Q= 0)между системой и окружающей средой. К адиабатическим процессам можно отнести все быстропротекающие процессы. Например, адиабатическим процессом можно считать процесс распространения звука в среде, так как скорость распространения звуковой волны настолько велика, что обмен энергией между волной и средой произойти не успевает. Адиабатические процессы применяются в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т. д.Из первого начала термодинамики (Q= d U+A) для адиабатического процесса следует, что 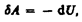т. е. внешняя работа совершается за счет изменения внутренней энергии системы 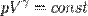… -уравнения адиабат. Процесса. называется показателем адиабаты (или коэффициентом Пуассона). Рассмотренные изохорный, изобарный, изотермический и адиабатический процессы имеют общую особенность — они происходят при постоянной теплоемкости. В первых двух процессах теплоемкости соответственно равны С_V и С _p, в изотермическом процессе (d T=0) теплоемкость равна ±, в адиабатическом (Q =0) теплоемкость равна нулю. Процесс, в котором теплоемкость остается постоянной, называется политропным.

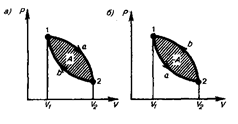
Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное. На диаграмме процессов цикл изображается замкнутой кривой (рис. 84). Цикл, совершаемый идеальным газом, можно разбить на процессы расширения (1 — 2) и сжатия (2 — 1) газа. Работа расширения (определяется площадью фигуры 1a2V ₂ V ₁ 1) положительна (d V >0), работа сжатия (определяется площадью фигуры 2b1V ₁ V ₂ 2) отрицательна (d V< 0 ). Следовательно, работа, совершаемая газом за цикл, определяется площадью, охватываемой замкнутой кривой. Если за цикл совершается положительная работа A= 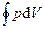> 0 (цикл протекает по часовой стрелке), то он называется прямым (рис. 84, а), если за цикл совершается отрицательная работа A= 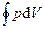< 0 (цикл протекает против часовой стрелки), то он называется обратным (рис. 84, б).

Прямой цикл используется в тепловых двигателях — периодически действующих двигателях, совершающих работу за счет полученной извне теплоты. Обратный цикл используется в холодильных машинах — периодически действующих установках, в ко­торых за счет работы внешних сил теплота переносится к телу с более высокой температурой.

В результате кругового процесса система возвращается в исходное состояние и, следовательно, полное изменение внутренней энергии газа равно нулю. Поэтому первое начало термодинамики для кругового процесса т. е. работа, совершаемая за цикл, равна количеству полученной извне теплоты. Однако в результате кругового процесса система может теплоту как получать, так и отдавать, поэтому 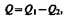где Q ₁ — количество теплоты, полученное системой, Q ₂ — количество теплоты, отданное системой. Поэтому термический коэффициент полезного действия для кругового процесса

Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении, причем если такой процесс происходит сначала в прямом, а затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среда и в этой системе не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым.

Любой равновесный процесс является обратимым. Обратимость равновесного процесса, происходящего в системе, следует из того, что се любое промежуточное состояние есть состояние термодинамического равновесия; для него «безразлично», идет процесс в прямом или обратном направлении. Реальные процессы сопровождают­ся диссипацией энергии (из-за трения, теплопроводности и т. д.), которая нами не обсуждается. Обратимые процессы — это идеализация реальных процессов. Их рассмот­рение важно по двум причинам: 1) многие процессы в природе и технике практически обратимы; 2) обратимые процессы являются наиболее экономичными; имеют максимальный термический коэффициент полезного действия, что позволяет указать пути повышения к. п. д. реальных тепловых двигателей

Понятие энтропии введено в 1865 г. Р. Клаузиусом. Для выяснения физического содержания этого понятия рассматривают отношение теплоты Q, полученной телом в изотермическом процессе, к температуре Т теплоотдающего тела, называемое приведенным количеством теплоты.

Приведенное количество теплоты, сообщаемое телу на бесконечно малом участке процесса, равно Q/T. Строгий теоретический анализ показывает, что приведенное количество теплоты, сообщаемое телу в любом обратимом круговом процессе, равно нулю: 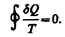(57.1)

Из равенства нулю интеграла (57.1), взятого по замкнутому контуру, следует, что подынтегральное выражение Q/T есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние. Таким образом, (57.2) Функция состояния, дифференциалом которой является Q/T, называется энтропией и обозначается S. Из формулы (57.1) следует, что для обратимых процессов изменение энтропии 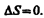(57.3)В термодинамике доказывается, что энтропия системы, совершающей необратимый цикл, возрастает: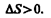

Таккак реальные процессы необратимы, то можно утверждать, что все процессы в замкнутой системе ведут к увеличению ее энтропии — принцип возрастания энтропии. При статистическом толковании энтропии это означает, что процессы в замкнутой системе идут в направлении увеличения числа микросостояний, иными словами, от менее вероятных состояний к более вероятным, до тех пор пока вероятность состояния не станет максимальной.

Работа газа теплоемкость Для рассмотрения конкретных процессов найдем в общем виде внешнюю работу, совершаемую газом при изменении его объема. Рассмотрим, например, газ, находящийся под поршнем в цилиндрическом сосуде (рис. 78). Если газ, расширяясь, пере­двигает поршень на бесконечно малое расстояние d l, то производит над ним работу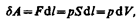

где S — площадь поршня, S d l=dV— изменение объема системы. Таким образом, (52.1)

Полную работу А, совершаемую газом при изменении его объема от V ₁ до V ₂, найдем интегрированием формулы (52.1): (52.2)Результат интегрирования определяется характером зависимости между давлением и объемом газа. Найденное для работы выражение (52.2) справедливо при любых изменениях объема твердых, жидких и газообразных тел.

Удельная теплоемкость вещества — величина, равная количеству теплоты, необходи­мому для нагревания 1 кг вещества на 1 К: Единица удельной теплоемкости — джоуль на килограмм-кельвин (Дж/(кг  К)). Молярная теплоемкость —величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К: (53.1)где = m / М — количество вещества.

Единица молярной теплоемкости — джоуль на моль-кельвин (Дж/(моль  К)). Удельная теплоемкость с связана с молярной С _m, соотношением 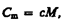(53.2)

где М — молярная масса вещества.Различают теплоемкости при постоянном объеме и постоянном давлении, если в процессе нагревания вещества его объем или давление поддерживается постоянным.

Запишем выражение первого начала термодинамики (51.2) для 1 моль газа с учетом формул (52.1) и (53.1): 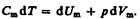(53.3)Если газ нагревается при постоянном объеме, то работа внешних сил равна нулю (см. (52.1)) и сообщаемая газу извне теплота вдет только на увеличение его внутренней энергии: (53.4)т. е. молярная теплоемкость газа при постоянном объеме С_V равна изменению внут­ренней энергии 1 моль газа при повышении его температуры на 1 К. Согласно формуле (50.1), тогда (53.5)Если газ нагревается при постоянном давлении, то выражение (53.3) можно запи­сать в виде Учитывая, что не зависит от вида процесса (внутренняя энергия идеального газа не зависит ни от p, ни от V, а определяется лишь температурой Т) и всегда равна С_V (см. (53.4)), и дифференцируя уравнение Клапейрона — Менделеева pV_m=RT (42.4) по T (p =const), получаем (53.6)Выражение (53.6) называется уравнением Майера; оно показывает, что С_р всегда больше С_V на величину молярной газовой постоянной. Это объясняется тем, что при нагрева­нии газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, таккак постоянство давления обеспечивается увеличением объема газа. Использовав (53.5), выражение (53.6) можно записать в виде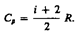

Второе начало термодинамики

Используя понятие энтропии и неравенство Клаузиуса, второе начало термодинамики можно сформулировать как закон возрастания энтропии замкнутой системы при необратимых процессах: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает.

Укажем еще две формулировки второго начала термодинамики:

1) по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу;

2) по Клаузиусу: невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому.

Первые два начала термодинамики дают недостаточно сведений о поведении термодинамических систем при нуле Кельвина. Они дополняются третьим началом термодинамика, или теоремой Нернста* — Планка: энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина: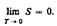

Тепловые двигатели и холодильные машины.

Из формулировки второго начала термодинамики по Кельвину следует, что вечный двигатель второго рода — периодически действующий двигатель, совершающий работу за счет охлаждения одного источника теплоты, — невозможен. Для иллюстрации этого положения рассмотрим работу теплового двигателя (исторически второе начало термодинамики и возникло из анализа работы тепловых двигателей).

Принцип действия теплового двигателя приведен на рис. 85. От термостата* с более высокой температурой Т ₁, называемого нагревателем, за цикл отнимается количество теплоты Q ₁, а термостату с более низкой температурой Т ₂, называемому холодильником, за цикл передается количество теплоты Q ₂, при этом совершается работа А = Q ₁ – Q ₂.

Процесс, обратный происходящему в тепловом двигателе, используется в холо­дильной машине, принцип действия которой представлен на рис. 86. Системой за цикл от термостата с более низкой температурой Т ₂ отнимается количество теплоты Q ₂ и от­дается термостату с более высокой температурой Т ₁ количество теплоты Q ₁. Для кругового процесса, согласно (56.1), Q=A, но, по условию, Q = Q ₂ – Q ₁< 0, поэтому А< 0 и Q ₂ – Q ₁= –А, или Q ₁ = Q ₂ + A, т. е. количество теплоты Q ₁, отданное системой источнику теплоты при более высокой температуре T ₁ больше количества теплоты Q ₂, полученного от источника теплоты при более низкой температуре T ₂, на величину работы, совершенной над системой. Следовательно, без совершения работы нельзя отбирать теплоту от менее нагретого тела и отдавать ее более нагретому. Это утверждение есть не что иное, как второе начало термодинамики в формулировке Клаузиуса.

Основываясь на втором начале термодинамики, Карно вывел теорему, носящую теперь его имя: из всех периодически действующих тепловых машин, имеющих оди­наковые температуры нагревателей (T ₁) и холодильников (T ₂), наибольшим к. п. д. обладают обратимые машины; при этом к. п. д. обратимых машин, работающих при одинаковых температурах нагревателей (T ₁) и холодильников (T ₂), равны друг другу и не зависят от природы рабочего тела (тела, совершающего круговой процесс и обменивающегося энергией с другими телами), а определяются только температурами нагревателя и холодильника.

Карно теоретически проанализировал обратимый наиболее экономичный цикл, состоящий из двух изотерм и двух адиабат. Его называют циклом Карно. Рассмотрим прямой цикл Карно, в котором в качестве рабочего тела используется идеальный газ, заключенный в сосуд с подвижным поршнем.

Цикл Карно изображен на рис. 87, где изотермические расширение и сжатие заданы соответственно кривыми 1 — 2 и 3—4, а адиабатические расширение и сжатие — кривыми 2 — 3 и 4—1. При изотермическом процессе U= const, поэтому, согласно (54.4), количество теплоты Q ₁, полученное газом от нагревателя, равно работе расширения А ₁₂, совершаемой газом при переходе из состояния 1 в состояние 2:

(59.1)

При адиабатическом расширении 2 — 3 теплообмен с окружающей средой отсутствует и работа расширения А ₂₃ совершается за счет изменения внутренней энергии (см. (55.1) и (55.8)):

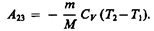
Количество теплоты Q ₂, отданное газом холодильнику при изотермическом сжатии, равно работе сжатия А ₃₄:

(59.2)

Работа адиабатического сжатия

Работа, совершаемая в результате кругового процесса,

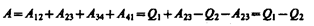
и, как можно показать, определяется площадью, заштрихованной на рис. 87. Термический к. п. д. цикла Карно, согласно (56.2),

Применив уравнение (55.5) для адиабат 2 — 3 и 4—1, получим

откуда

(59.3)

Подставляя (59.1) и (59.2) в формулу (56.2) и учитывая (59.3), получаем

(59.4)

Согласно теореме Карно, химический состав рабочего тела не влияет на результаты сравнения температур, поэтому такая термодинамическая шкала не связана со свойствами какого-то опреде­ленного термометрического тела. Отметим, что практически таким образом сравни­вать температуры трудно, так как реальные термодинамические процессы, как ухе указывалось, являются необратимыми.

Идеальные газы

Модель идеального газа, используемая в молекулярно-кинетической теории газов, позволяет описывать поведение разреженных реальных газов при достаточно высоких температурах и низких давлениях. При выводе уравнения состояния идеального газа размерами молекул и их взаимодействием друг с другом пренебрегают. Повышение давления приводит к уменьшению среднего расстояния между молекулами, поэтому необходимо учитывать объем молекул и взаимодействие между ними. Taк, в 1 м³ газа при нормальных условиях содержится 2,6810²⁵ молекул, занимающих объем пример­но 10^–4 м³ (радиус молекулы примерно 10^–10 м), которым по сравнению с объемом газа (1 м³) можно пренебречь. При давлении 500 МПа (1 атм = 101,3 кПа) объем молекул составит уже половину всего объема газа. Таким образом, при высоких давлениях и низких температурах указанная модель идеального газа непригодна.

При рассмотрении реальных газов — газов, свойства которых зависят от взаимо­действия молекул, надо учитывать силы межмолекулярного взаимодействия. Они прояв­ляются на расстояниях  10^–9 м и быстро убывают при увеличении расстояния между молекулами. Такие силы называются короткодействующими.

для реальных газов необходимо учитывать размеры молекул и их взаимодействие друг с другом, поэтому модель идеального газа и уравнение Клапейрона — Менделеева (42.4) pV _m =RT (для моля газа), описывающее идеальный газ, для реальных газов непригодны.

Учитывая собственный объем молекул и силы межмолекулярного взаимодействия, голландский физик И. Ван-дер-Ваальс (1837—1923) вывел уравнение состояния реального газа. Ван-дер-Ваальсом в уравнение Клапейрона — Менделеева введены две поправки.

1. Учет собственного объема молекул. Наличие сил отталкивания, которые проти­водействуют проникновению в занятый молекулой объем других молекул, сводится к тому, что фактический свободный объем, в котором могут двигаться молекулы реального газа, будет не V _m, а V _m — b, где b — объем,занимаемый самими молекулами.

Объем b равен учетверенному собственному объему молекул. Если, например, в сосуде находятся две молекулы, то центр любой из них не может приблизиться к центру другой молекулы на расстояние, меньшее диаметра d молекулы. Это означает, что для центров обеих молекул оказывается недоступным сферический объем радиуса d, т. е. объем, равный восьми объемам молекулы или учетверенному объему молекулы в рас­чете на одну молекулу.

2. Учет притяжения молекул. Действие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением. По вычислени­ям Ван-дер-Ваальса, внутреннее давление обратно пропорционально квадрату моляр­ного объема, т. е. 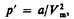(где а — постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного при­тяжения, V _m — молярный объем.Вводя эти поправки, получим уравнение Ван-дер-Ваальса для моля газа (уравнение состояния реальных газов):

Волновые процессы. Продольные и поперечные волны. Длина волны, скорость, частота (связь между этими величинами). Уравнение бегущей волны. Уравнение стоячей волны. Интерференция волн. Электромагнитные волны

Волновые процессы. Продольные и поперечные волны. Длина волны, скорость, частота (связь между этими величинами). Колебания, возбужденные в какой-либо точке среды (твердой, жидкой или газообразной), распространяются в ней с конечной скоростью, зависящей от свойств среды, передаваясь от одной точки среды к другой. Чем дальше расположена частица среды от источника колебаний, тем позднее она начнет колебаться. Иначе говоря, фазы колеба­ний частиц среды и источника тем больше отличаются друг от друга, чем больше это расстояние. При изучении распространения колебаний не учитывается дискретное (молекулярное) строение среды и среда рассматривается как сплошная, т. е. непрерыв­но распределенная в пространстве и обладающая упругими свойствами. Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной). При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества. Среди разнообразных волн, встречающихся в природе и технике, выделяются следующие их типы: волны на поверхности жидкости, упругие и электромагнитные волны. Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и попереч­ные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных — в плоскостях, перпендикулярных направлению распространения волны. Продольные волны могут возбуждаться в средах, в которых возникают упругие силы при деформации сжатия и растяжения, т. е. твердых, жидких и газообразных телах. Поперечные волны могут возбуждаться в среде, в которой возникают упругие силы при деформации сдвига, т. е. в твердых телах; в жидкостях и газах возникают только продольные волны, а в твердых телах — как продольные, так и поперечные. Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими. Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны l. Длина волны равна тому расстоянию, на которое распространяется определенная фаза колебания за период. или, учитывая, что T = 1/ n, где n — частота колебаний,

Уравнение бегущей волны. Бегущими волнами называются волны, которые переносят в пространстве энергию. Перенос энергии волнами количественно характеризуется вектором плотности потока энергии. Этот вектор для упругих волн называется вектором Умова. Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны. Для вывода уравнения бегущей волны — зависимости смещения колеблющейся частицы от координат и времени — рассмотрим плоскую волну, предполагая, что колебания носят гармонический характер, а ось х совпадает с направлением распрост­ранения волны. В данном случае волновые поверхности перпендикулярны оси х, а так как все точки волновой поверхности колеблются одинаково, то сме­щение x будет зависеть только от x и t, т. е. x = x (x, t). Если колебания точек, лежащих в плоскости х= 0,описываются функцией x (0, t) = A cos wt, то частица В среды колеблется по тому же закону, но ее колебания будут отставать по времени от колебаний источника на t, так как для прохождения волной расстояния х требуется время t = x / v, где v — скорость распространения волны. Тогда уравнение колебаний частиц, лежащих в плоскости х, имеет вид . Уравнение есть уравнение бегущей волны.

Дата добавления: 2015-04-24