
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема 26.2. +28.5. Пусть в окрестности точки существуют и непрерывны , … и пусть существует . Тогда при
|
|
|
|
◄ Обозначим 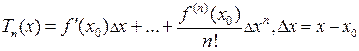 ,
, 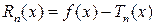 и рассмотрим отношение
и рассмотрим отношение 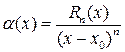 . По правилу Лопиталя(теореме 28.1), применённому
. По правилу Лопиталя(теореме 28.1), применённому 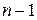 раз, имеем
раз, имеем
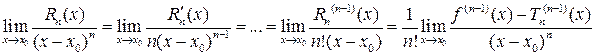 .Из определения
.Из определения 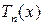 следует, что
следует, что 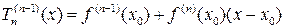 . Поэтому
. Поэтому 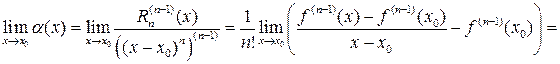
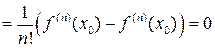 .Это означает, что
.Это означает, что 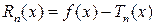 =
= 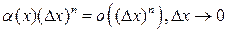 , что и требовалось доказать. ►
, что и требовалось доказать. ►
Вопрос 27. РАЗЛОЖЕНИЯ ФУНКЦИЙ ex, sinx, cosx, lnx, (1+x)µ
Применим доказанные формулы Тейлора к функциям, перечисленным выше.
1) Так как 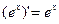 , для всех
, для всех 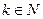 выполняется равенство
выполняется равенство
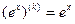 .Следовательно, все эти производные равны 1 при x=0.
.Следовательно, все эти производные равны 1 при x=0.
Поэтому 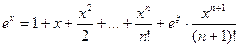 , где ξ – некоторая точка между 0 и x. Другая запись для точки ξ: ξ = θ x, 0 < q <1. Это – разложение ex с остаточным членом в форме Лагранжа.
, где ξ – некоторая точка между 0 и x. Другая запись для точки ξ: ξ = θ x, 0 < q <1. Это – разложение ex с остаточным членом в форме Лагранжа.
Формула Тейлора с остаточным членом в форме Пеано для ex принимает вид
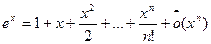 ,
, 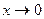 .
.
2)Перейдём к функциям sinx, cosx:
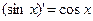 ,
, 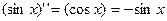 ,
, 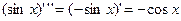 ,
, 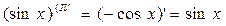 и т.д.
и т.д.
Эти равенства означают, что 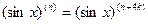 для любого
для любого 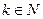 . Поэтому имеет место формула
. Поэтому имеет место формула 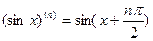 , которую легко проверить для n=0,1,2,3, а для остальных n она верна ввиду установленного равенства
, которую легко проверить для n=0,1,2,3, а для остальных n она верна ввиду установленного равенства 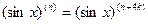 .
.
Поэтому при x=0 имеем:
производная порядка 4k равна 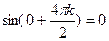 ;
;
производная порядка 4k+1 равна 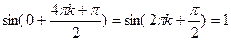 ;
;
производная порядка 4k+2 равна 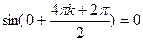 ;
;
производная порядка 4k+2 равна 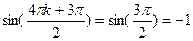 .
.
Следовательно,
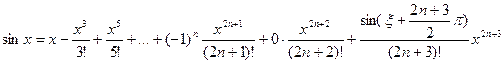 , где ξ лежит между 0 и x.
, где ξ лежит между 0 и x.
Здесь – небольшая хитрость. Мы разложили функцию до членов степени 2n+2, что позволило сделать погрешность меньшей. Конечно, член 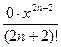 выписывать не надо, он равен 0, а здесь он был помещён только для разъяснения вышеупомянутой «хитрости». Итак
выписывать не надо, он равен 0, а здесь он был помещён только для разъяснения вышеупомянутой «хитрости». Итак 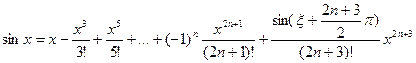 .
.
Аналогично,
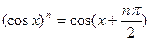 и
и
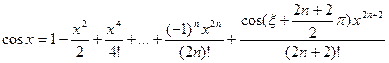
Разложения для sinx и cosx по формуле Тейлора с остаточным членом в форме Пеано имеют вид:
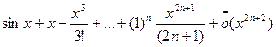 , x→0
, x→0
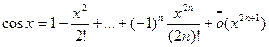 , x→0
, x→0
3) Перейдём к функции 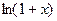 . Её последовательные производные равны:
. Её последовательные производные равны:
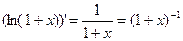 ,
,
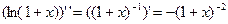 и т.д.
и т.д.
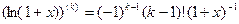
Вычисленная при х=0, производная порядка k равна 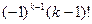
Поэтому
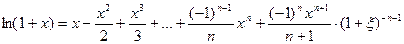 ,
,
где ξ – некоторая точка между 0 и х.
Разложение с остаточным членом в форме Пеано имеет вид:
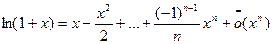
4) Наконец, вычислим последовательные производные функции 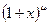 :
:
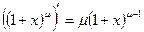 ,
, 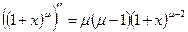 ,
,  ,
, 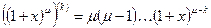 .
.
Вычисленная в точке  , производная порядка
, производная порядка 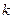 равна
равна 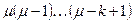 .
.
Поэтому формула Тейлора с остаточным членом в форме Лагранжа имеет вид:
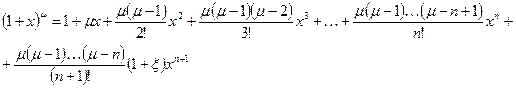 ,
,
где 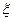 - между
- между 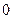 и
и 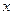 . Это так называемое биноминальное разложение с остаточным членом в форме Лагранжа. Та же формула с остаточным членом в форме Пеано имеет вид:
. Это так называемое биноминальное разложение с остаточным членом в форме Лагранжа. Та же формула с остаточным членом в форме Пеано имеет вид:
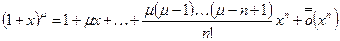 ,
, 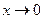 .
.
В качестве примера применения формулы Тейлора рассмотрим задачу нахождения 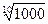 с точностью до 0,001.
с точностью до 0,001.
Сначала подготовим ее к применению формулы Тейлора. Для этого, зная, что 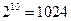 , перепишем вычисляемую величину в виде
, перепишем вычисляемую величину в виде 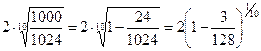 .
.
Используем биноминальное разложение при
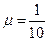 ,
, 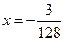 .
.
Число 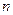 членов разложения выберем, исходя из заданной точности. Для этого найдем
членов разложения выберем, исходя из заданной точности. Для этого найдем 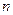 такое, чтобы:
такое, чтобы:

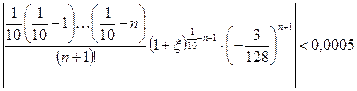 (1)
(1)
(тогда при умножении на стоящий впереди коэффициент 2 получаем требуемую точность 0,001).
Очевидно, что:
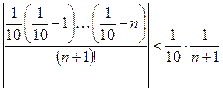 ;
;
Далее, 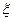 - между
- между 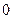 и
и 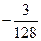 , поэтому
, поэтому 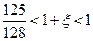 и
и 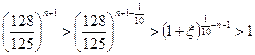 ,
,
поэтому
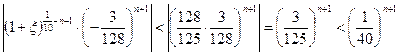
Итак, абсолютная величина левой части неравенства (1) не больше, чем
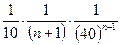 . (2)
. (2)
Поэтому если число (2) окажется меньше, чем 0,0005, то и остаточный член формулы будет меньше 0,0005 и требуемая точность будет достигнута.
Сразу ясно, что при 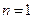
Число 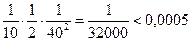 .
.
Поэтому требуемую точность для приближенной величины даёт приближённая формула:
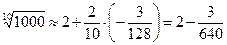 .
.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 399; Нарушение авторских прав?; Мы поможем в написании вашей работы!