Тогда и

Вопрос 28: ПРАВИЛА ЛОПИТАЛЯ

Приведённые ниже теоремы принадлежат, в основном, Лопиталю (G.F.de l’Hospitale) и И.Бернулли (Joh.Bernoulli).

1. Неопределённость типа

Теорема 28.1. Пусть: 1) функции f(x) и g(x) определены в промежутке (a, b], 2) 3) в промежутке (a, b] существуют конечные производные f’(x) и g’(x), причём g’(x) ≠ 0, и наконец, 4) существует (конечный или нет) предел

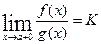
Доказательство.◄ Дополним определение функций f(x) и g(x), положив их при x = a равными нулю: f(a) = g(a) = 0. Тогда эти функции окажутся непрерывными во всём замкнутом промежутке [a, b]: их значения в точке a совпадают с пределами при x→a + 0 [ввиду 2)], а в прочих точках непрерывность вытекает из существования конечных производных [см. 3)]. Применяя теорему Коши, получим

,

где a‹c‹x. То обстоятельство, что g(x) ≠ 0, т. е. g(x) ≠ g(a), есть следствие предположения: g′(x) ≠ 0, как это было установлено при выводе формулы Коши.

Когда x→a, очевидно, и с→a, так что, в силу 4),

,

что и требовалось доказать.►

Таким образом, доказанная теорема сводит предел отношения функций к пределу отношения производных, если последний существует. Часто оказывается, что нахождение предела отношения производных проще и может быть осуществлено элементарными приёмами.

Теорема 1 легко распространяется на случай, когда аргумент x стремится к бесконечному пределу: a = 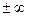. Именно, имеет место, например.

Теорема 28.2. Пусть: 1) функции f(x) и g(x) определены в промежутке [c, +∞), где с›0, 2) 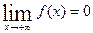, , 3) существуют в промежутке [c, +∞) конечные производные f′(x) и g′(x), причём g′(x) ≠ 0, и, наконец, 4) существует (конечный или нет) предел

Дата добавления: 2015-04-24