
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Устойчивость разностной схемы
|
|
|
|
Аппроксимация с порядком.
Сходимость разностной схемы с порядком.
Решение 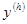 сходится к
сходится к  с порядком
с порядком  , если
, если 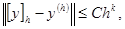 .
.
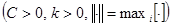 .
.
Пусть задача 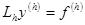 имеет единственное решение.
имеет единственное решение.
Пусть 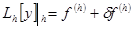 (
( - невязка).
- невязка).
Разностная задача аппроксимирует дифференциальную задачу на решении
 с порядком
с порядком  , если
, если 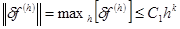 .
.
Пример. Рассмотрим схему Эйлера для задачи  .
.
Разностная задача  ,
, 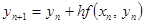 ,
,
 . Поэтому
. Поэтому
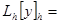
 =
=  . То есть,
. То есть,  , следовательно, схема Эйлера дает аппроксимацию первого порядка.
, следовательно, схема Эйлера дает аппроксимацию первого порядка.
Замечание. Ошибку аппроксимации  можно оценить по правилу Рунге, решая дифференциальное уравнение с шагом
можно оценить по правилу Рунге, решая дифференциальное уравнение с шагом 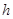 , а затем с шагом
, а затем с шагом  и сравнивая решения:
и сравнивая решения: 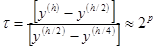 , где
, где  - порядок аппроксимации.
- порядок аппроксимации.
Разностная схема называется устойчивой, если 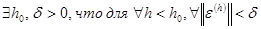 разностная задача
разностная задача  имеет единственное решение
имеет единственное решение  такое, что
такое, что  .
.
Другими словами, при малых возмущениях 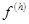 мало возмущается
мало возмущается 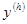 .
.
Теорема. Пусть разностная схема аппроксимирует дифференциальную задачу на решении  с порядком
с порядком  и устойчива. Тогда решение разностной задачи сходится к
и устойчива. Тогда решение разностной задачи сходится к  с порядком
с порядком  , причем
, причем 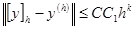 . Здесь
. Здесь  - константа аппроксимации, С – константа устойчивости.
- константа аппроксимации, С – константа устойчивости.
Доказательство. Пусть 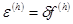 , тогда по единственности решения (определение устойчивости) и определению аппроксимации
, тогда по единственности решения (определение устойчивости) и определению аппроксимации  . Тогда
. Тогда
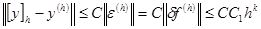 (при
(при 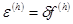 имеем
имеем 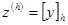 ).
).
Содержание.
Лекция 1 Неопределенный интеграл, таблица интегралов. 2
Лекция 2. Методы интегрирования и таблица интегралов. 4
Лекция 3. Интегрирование рациональных функций. 8
Лекция 4. Интегрирование иррациональных и 14
тригонометрических функций.
Лекция 5. Определенный интеграл. 18
Лекция 6. Формула Ньютона – Лейбница. 22
Лекции 7, 8 Несобственные интегралы. 25
Лекции 9-10. Приложения определенного интеграла. 32
Лекция 11. Дифференциальные уравнения. 37
Лекция 12. Основные типы дифференциальных уравнений 39
первого порядка.
Лекция 13. Геометрическая интерпретация дифференциальных 47
уравнений 1 порядка, изоклины. Особые точки и особые
решения.
Лекция 14. Дифференциальные уравнения высших порядков. 50
Лекции 15–16. Линейные дифференциальные уравнения 53
n –ого порядка с переменными коэффициентами.
Лекции 17-18. Линейные дифференциальные уравнения с 61
постоянными коэффициентами.
Лекции 19-20. Нормальные системы дифференциальных уравнений. 68
Лекция 21. Системы линейных дифференциальных уравнений. 76
Лекция 22. Однородные системы линейных дифференциальных 82 уравнений с постоянными коэффициентами.
Лекции 23-24. Устойчивость движения, классификация точек покоя, 87
теоремы Ляпунова.
Лекция 25. Приближенное вычисление интеграла. 95
Лекция 26. Обзор численных методов решения задачи Коши 98
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 744; Нарушение авторских прав?; Мы поможем в написании вашей работы!