Сходимость, устойчивость разностных схем, порядок точности методов

.

Методы Адамса.

Идея методов Адамса – использовать не промежуточные вычисления значений правой части дифференциального уравнения внутри отрезка 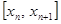, а значения правой части на предыдущих шагах (сделать метод методом «с памятью»).

В формуле 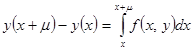заменим 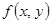интерполяционным полиномом Ньютона .

Явные методы Адамса (Адамса – Башфорта).

Возьмем 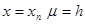, но интеграл будем брать по предыдущему отрезку 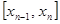. Тогда

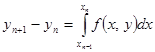
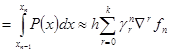
Здесь 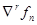- конечная разность 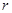- го порядка:

Подставляя эти разности, получим

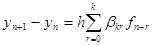(k – шаговый явный метод Адамса – Башфорта)

Пример. 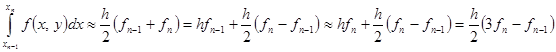Получен явный метод Адамса – Башфорта второго порядка ( двухшаговый )

Более точен метод Адамса – Башфорта четвертого порядка:

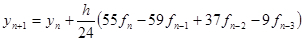
Заметим, если 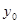задано (в задаче Коши начальное условие задается), то для того, чтобы начал работать метод Адамса 4 порядка, нужно вычислить еще значения (каким-либо другим методом) 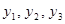. Тогда из системы формул Адамса Башфорта, выписанных для 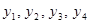, вычисляются значения правых частей 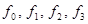, необходимые для того, чтобы метод начал работать. Затем уже по этим значениям по формуле метода определяются .

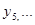Эта процедура называется «разгоном метода» и является обязательной в методах Адамса.

Неявные методы Адамса (Адамса – Мултона).

Возьмем 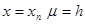, интеграл будем брать по отрезку 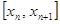. Тогда

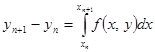
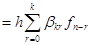
Здесь 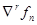- конечная разность 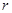- го порядка:

Подставляя эти разности, получим

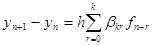(k – шаговый явный метод Адамса –Мултона)

Формально он записан в том же виде, что и метод Адамса – Башфорта, но разница существенна: в методе Адамса – Мултона в левой части уравнения присутствует 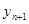, а в правой части присутствует 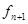. Поэтому приходится еще решать систему уравнений для явного определения .

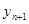Пример. 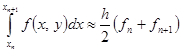. Поэтому имеем формулу

метода Адамса – Мултона второго порядка.

Более точен метод Адамса – Мултона четвертого порядка

.

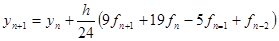Эти методы также требуют разгона.

Обобщением методов Адамса являются линейные многошаговые методы

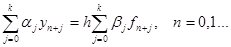
Если 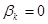, то метод – явный, если 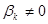, то метод – неявный.

Есть методы, сочетающие явные и неявные этапы – методы. Таковы, например, методы типа предиктор – корректор (предиктор P – предсказатель – явный метод, корректор С – неявный метод). Эти методы содержат обычно и этапы вычисления функции Е. Распространены методы РЕСЕ и РЕС.

Рассмотрим в качестве метода Р метод Адамса – Башфорта 2 го порядка, а в качестве метода С – метод Адамса – Мултона 2 го порядка.

Схема метода может быть записана в виде.

Р .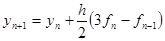

Е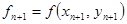

С

Е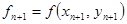

Метод Р «предсказывает», прогнозирует 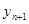, вычисляется значение правой части, которое используется в методе С – «корректоре» для коррекции приближения 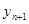, затем вычисляется более точное значение правой части, которое вновь используется в методе Р.

Вообще-то это – тема отдельного курса, но нельзя говорить о методах решения дифференциальных уравнений и не сказать хотя бы несколько слов о сходимости численных алгоритмов, устойчивости вычислительных схем и точности методов.

Рассмотрим дифференциальное уравнение 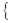, равномерную сетку на отрезке интегрирования .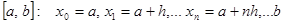

Рассмотрим сеточную функцию 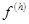- правую часть уравнения, определенную на сетке .

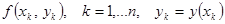Введем аппроксимации производной:

, , .

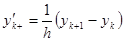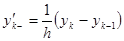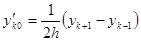Задача Коши (дифференциальная задача) 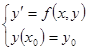заменяется разностной задачей (разностной схемой)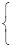

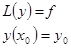
или .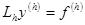

Разностная схема отличается от дифференциального уравнения тем, что функции заменены сеточными, производные заменены их аппроксимациями.

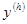- решение разностной задачи, - решение дифференциальной задачи, 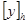- сеточная функция, построенная по .

Дата добавления: 2015-04-24