Гармонические колебания и их характеристики

Механические и электромагнитные колебания

Колебания и волны

Глава 18

Колебаниями называются движения или процессы, которые характеризуются опре­деленной повторяемостью во времени. Ко­лебательные процессы широко распро­странены в природе и технике, например качание маятника часов, переменный электрический ток и т. д. При колебатель­ном движении маятника изменяется ко­ордината его центра масс, в случае пере­менного тока колеблются напряжение и ток в цепи. Физическая природа колеба­ний может быть разной, поэтому различа­ют колебания механические, электромаг­нитные и др. Однако различные колеба­тельные процессы описываются одинако­выми характеристиками и одинаковыми уравнениями. Отсюда следует целесооб­разность единого подхода к изучению ко­лебаний различной физической природы. Например, единый подход к изучению ме­ханических и электромагнитных колеба­ний применялся английским физиком Д. У. Рэлеем (1842—1919), А. Г. Столето­вым, русским инженером-экспериментато­ром П.Н.Лебедевым (1866—1912). Боль­шой вклад в развитие теории колебаний внесли советский физик Л. И. Мандель­штам (1879- -1944) и его ученики.

Колебания называются свободными (или собственными), если они совершают­ся за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему (систему, совершающую колебания). Простейшим типом колебаний явля­ются гармонические колебания — колеба­ния, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Рассмотрение гармонических колебаний важно но двум причинам: 1) колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому; 2) различные периоди­ческие процессы (процессы, повторяющие­ся через равные промежутки времени) можно представить как наложение гармо­нических колебаний. Гармонические коле­бания величины s описываются уравнени­ем типа.

s= A cos(w₀t+j), (140.1)

где А - максимальное значение колеблю­щейся величины, называемое амплитудой колебаний, w₀ круговая (циклическая) частотой, j- начальная фаза колебаний

в момент времени t=0, (w₀t+j)— фаза колебаний в момент времени t. Так как косинус изменяется в пределах от +1 до -1, то s может, принимать значения от + А до - А.

Определенные состояния системы, совершающей гармонические колебания, по­вторяются через, промежуток времени Т, называемый периодом колебания, за кото­рый фаза колебания получает приращение 2p, т. е.

w₀(t+T ) +j=(w₀t +j)+2p,

откуда

T=2p/w₀. (140.2)

Величина, обратная периоду коле­баний,

v=1/T, (140.3)

т. о. число полных колебаний, совершае­мых в единицу времени, называется часто­той колебаний. Сравнивая (140.2) и (140.3), получим

w₀=2pv.

Единица частоты — герц (Гц):1Гц — частота периодического процесса, при ко­торой за 1 с совершается один цикл про­цесса.

Запишем первую и вторую производ­ные по времени от гармонически колеблю­щейся величины s (соответственно ско­рость и ускорение):

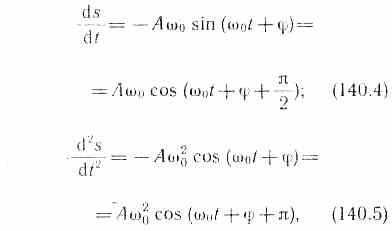
т. е. имеем гармонические колебания с той же циклической частотой. Амплитуды ве­личин (140.4) и (140.5) соответственно равны А w₀ и A w²₀. Фаза скорости (140.4) отличается от фазы величины (140.1) на π/2, а фаза ускорения (140.5) отличается от фазы величины (140.1) на p. Следова­тельно, в моменты времени, когда s=0,

ds/dt приобретает наибольшие значения;

когда же s достигает максимального отрицательного значения, то d²s/dt² приобретает

наибольшее положительное значение (рис. 198).

Из выражения (140.5) следует диффе­ренциальное уравнение гармонических ко­лебаний

d²s/dt²+w²₀s=0 (140.6)

(где учтено, что s=A cos(w₀t+j)). Решением этого уравнения является выражение (140.1).

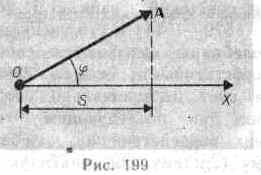
Гармонические колебания изобража­ются графически методом вращающегося вектора амплитуды, или методом вектор­ных диаграмм. Для этого из произвольной точки О, выбранной на оси х, под.углом j, равным начальной фазе колебания, откла­дывается вектор А, модуль которого равен амплитуде А рассматриваемого колебания (рис. 199). Если этот вектор привести во вращение с угловой скоростью w₀, то про­екция конца вектора будет перемещаться по оси х и принимать значения от - A до + А, а колеблющаяся величина будет из­меняться со временем по закону s= A cos(w₀t+j). Таким образом, гармо­ническое колебание можно представить проекцией на некоторую произвольно выбранную ось вектора амплитуды А, от­ложенного из произвольной точки оси под углом j, равным начальной фазе, и вра­щающегося с угловой скоростью w₀ вокруг этой точки.

В физике часто применяется другой метод, который отличается от метода вра­щающегося вектора амплитуды лишь по форме. В этом методе колеблющуюся ве­личину представляют комплексным чис­лом. Согласно формуле Эйлера, для ком­плексных чисел

e^iia=cosa+ i sina, (140.7)

где i=Ö-1 — мнимая единица. Поэтому уравнение гармонического колебания (140.1) можно записать в экспоненциаль­ной форме:

(140.8)

представляет собой гармоническое коле­бание. Обозначение Re вещественной части условимся опускать и (140.8) будем записывать в виде

В теории колебаний принимается, что ко­леблющаяся величина s равна веществен­ной части комплексного выражения, стоя­щего в этом равенстве справа.

Дата добавления: 2015-04-24