Наблюдатель пониженного порядка

Из предыдущего примера четко видно, что искать было излишне, так как . В тех случаях, когда некоторые координаты вектора совпадают с какими-либо из координат вектора 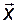, то очевидно, что рассматриваемый выше наблюдатель – наблюдатель полного порядка - выдает излишнюю информацию. Рассмотрим, каким образом можно получить наблюдатель с более простыми алгоритмами, полностью использующими информацию о векторе состояния 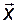, имеющуюся в векторе выхода . В более общем случае, когда вектор имеет размерность 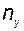, оказывается достаточным построить наблюдатель, порядок которого равен .

Пусть вектор имеет размерность 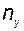и связан с вектором 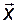равенством

, (3.11.19)

или

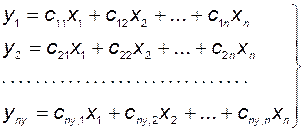. (3.11.20)

Если рассматривать как неизвестные, то здесь мы имеем 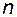неизвестных и 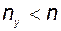уравнений. Таким образом, недостаёт 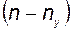уравнений. Полагаем, что , т. е. все строки матрицы линейно независимы. Введем 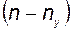- мерный вектор 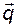, дополнив матрицу до квадратной невырожденной матрицы с помощью матрицы :

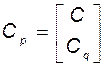. (3.11.21)

Запишем

, (3.11.22)

откуда следует

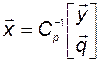. (3.11.23)

Обозначим

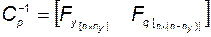, (3.11.24)

тогда

. (3.11.25)

Если удастся найти оценку 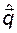вектора 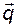, то можно будет вычислить оценку вектора состояния

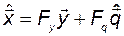. (3.11.26)

Так как 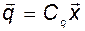, то

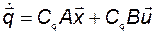. (3.11.27)

Подставим сюда 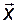из (3.11.26):

. (3.11.28)

Построим наблюдатель для вектора 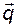. В последнем уравнении векторы 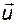и выступают в качестве входов. Если попытаться коррекцию наблюдателя ввести традиционным образом: , то получим

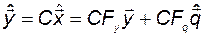. (3.11.29)

Но из (3.11.21) и (3.11.24) имеем

,

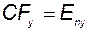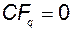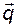откуда должно следовать ; , то есть и информации о здесь нет. Поэтому примем

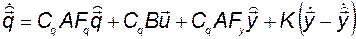. (3.11.30)

Проведем необходимые преобразования. Так как

,

то с учетом (3.11.26) получим

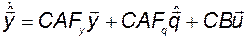. (3.11.31)

Проследим за поведением ошибки оценки

.

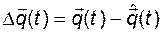Используя полученные выше выражения для 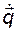и - (3.11.28) и (3.11.30), получим:

.

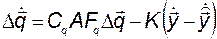Вычислим разность :

.

Так как выше было показано, что , то окончательно получим

, (3.11.32)

где матрица наблюдателя

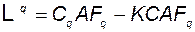. (3.11.33)

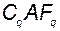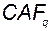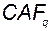Очевидно, что можно «заказать динамику обнуления ошибки», вы­бирая ( и - заданные матрицы). Матрицу следует выбирать таким образом, чтобы обеспечить заданное расположение собственных чисел наблюдателя. Если, например, , то имеет размер , а - и - . В этом случае задача решается аналогично расчету наблюдателя полного порядка со скалярным выходом.

Таким образом, рассчитав собственные значения матрицы , задавшись желаемыми собственными значениями наблюдателя пониженного порядка и получив соответствующие значения коэффициентов его характеристического полинома, легко записать выражение для матрицы в базисе идентификационного канонического представления. После этого потребуется перевести матрицу в исходный базис. Если известна пара матриц 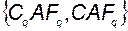, то через матрицы наблюдаемости в исходном базисе и в базисе идентификационного канонического представления и , причем должна быть построена с использованием пары матриц 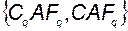, можно найти матрицу перехода от базиса 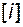к исходному базису .

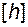Теперь следует позаботиться о реализуемости алгоритма наблюдателя. Из уравнения (3.11.30) с учетом (3.11.25) получим

. (3.11.34)

Это уравнение для реализации не годится, так как в случае его использования пришлось бы осуществлять операции дифференцирования вектора . В реальных условиях на вектор выхода объекта, как правило, наложены шумы измерений и другой физической природы. Эти шумы характеризуются широким спектром, и дифференцирование существенно увеличивает шумовую составляющую в выходном сигнале.

Для того чтобы не решать задачу измерения 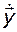, введем новую переменную , тогда

. (3.11.35)

Проведем соответствующую замену в (3.11.34) и в результате получим первое уравнение наблюдателя

. (3.11.36)

Теперь из уравнений (3.11.30) и (3.11.35) имеем

,

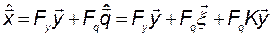или

. (3.11.37)

Это - второе уравнение наблюдателя. Таким образом, получено уравнение оценки вектора 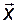с помощью наблюдателя пониженного порядка.

Дата добавления: 2015-03-31