Наблюдатель Люенбергера минимального порядка

Рассмотрим ещё один подход к формированию наблюдателя. Так же, как в п.3.11.2, сформируем матрицы , и введём вектор

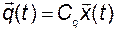. (3.11.38)

Оценку вектора 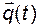будем искать как решение уравнения

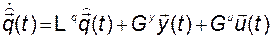, (3.11.39)

где , и 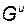- некоторые, пока неизвестные матрицы.

Как и прежде, ошибкой оценки вектора 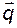будем считать разность

. (3.11.40)

В соответствии с уравнением объекта и выражением (3.11.38) запишем:

. (3.11.41)

Найдём дифференциальное уравнение для ошибки :

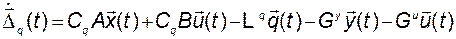. (3.11.42)

Добавим и вычтем в правой части последнего равенства и с учётом (3.11.38) получим

. (3.11.43)

Положим

(3.11.44)

и потребуем выполнения равенства

. (3.11.45)

Тогда получим уравнение для ошибки наблюдателя

. (3.11.46)

Если назначить матрицу так, чтобы её собственные числа лежали в левой полуплоскости достаточно далеко от мнимой оси, то ошибка наблюдателя, имеющая изначально место при ненулевых начальных условиях, будет с соответствующей скоростью стремиться к нулю. Так же быстро вектор

(3.11.47)

будет стремиться к вектору 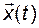. Вытекающее из (3.11.45) уравнение

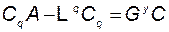a(3.11.48)

называется матричным уравнением Люенбергера.

Теперь учтём, что задача построения наблюдателя, то есть нахождения оценки вектора состояния 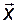, возникла из-за необходимости реализовать управление

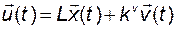. (3.11.49)

Сама по себе оценка вектора состояния часто не нужна. Поэтому попытаемся найти оценку линейной комбинации координат вектора состояния . Будем искать эту оценку в виде

. (3.11.50)

Так как с течением времени 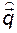стремится к 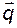, то с учётом (3.11.38) и уравнения выхода объекта получим

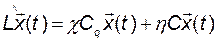, (3.11.51)

откуда следует

. (3.11.52)

Таким образом, необходимо решить следующую систему матричных уравнений:

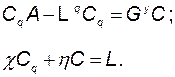(3.11.53)

Эта система всегда имеет решение, если, во-первых, собственные числа матриц и не совпадают друг с другом и, во-вторых, размерность вектора 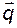(размерность матрицы наблюдателя )

, (3.11.54)

где 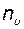- размер вектора управления; 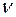- индекс наблюдаемости. Это такое число, для которого матрица

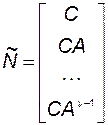(3.11.55)

имеет ранг, равный .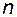

Таким образом, может быть сформулирован следующий итоговый алгоритм.

1. Найти индекс наблюдаемости 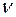и размерность наблюдателя .

2. Задать желаемую динамику наблюдателя и записать матрицу его динамики в виде матрицы, сопровождающей свой характеристический полином.

3. Вычислить матрицы согласно (3.11.53), а также матрицу согласно (3.11.44).

4. Реализовать алгоритмы регулятора, включая наблюдатель Люенбергера минимального порядка:

(3.11.56)

Дата добавления: 2015-03-31