
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формирование управления
|
|
|
|
Разделение исходного объекта на подсистемы интеграторов
Синтез управления в многомерной системе. Задача разделения каналов
В предыдущих разделах, посвящённых синтезу, рассматривались объекты со скалярным управлением (входом) и скалярным выходом. На практике встречаются и более сложные объекты. Один из них был упомянут в разделе 2.2. Это смесительный бак, у него две входные величины (два входных потока с различными концентрациями растворённого вещества) и две выходные (концентрация и расход выходного потока). В качестве другого примера может быть взят объект, связанный с перемоткой некоторой полосы с одного рулона на другой. Для этого объекта выходные переменные – это натяжение и линейная скорость перемотки; входные – напряжения или токи приводных двигателей моталки и разматывателя. Наконец, самолёт. В качестве выходных переменных могут выступать углы тангажа, курса и крена; в качестве входных, управляющих - угловые положения руля высоты, руля направления и элеронов.
Как правило, в таких объектах каждая выходная величина зависит от всех входных. В то же время при синтезе управления такими объектами часто требуется обеспечить не только заданные динамические и статические свойства системы, но и независимое управление по каждой из выходных переменных.
Пусть уравнения объекта имеют вид
 ; (3.10.1)
; (3.10.1)
 , (3.10.2)
, (3.10.2)
где размерность вектора состояния 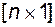 , вектор управления и вектор выхода имеют одинаковую размерность
, вектор управления и вектор выхода имеют одинаковую размерность  . Такую же размерность имеет вектор командного сигнала
. Такую же размерность имеет вектор командного сигнала 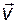 , поступающий на вход системы.
, поступающий на вход системы.
Требуется синтезировать управление 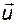 такое, чтобы:
такое, чтобы:
1) i –я составляющая вектора выхода 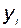 зависела только от i –й составляющей командного сигнала
зависела только от i –й составляющей командного сигнала 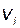 ;
;
|
|
|
2) по каждому из каналов была обеспечена заданная динамика, иными словами, передаточная функция 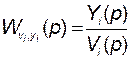 , имеющая заданные полюсы;
, имеющая заданные полюсы;
3) для каждого из каналов был обеспечен заданный статический коэффициент передачи.
Представим (3.10.2) в виде
 ,
,
где 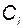 - строки матрицы
- строки матрицы  . Тогда
. Тогда 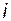 -я координата вектора выхода
-я координата вектора выхода
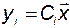 .
.
Рассмотрим процедуру многократного дифференцирования координат вектора выхода:
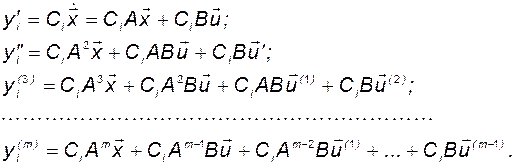 (3.10.3)
(3.10.3)
Сократим запись:
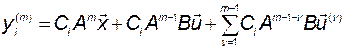 . (3.10.4)
. (3.10.4)
Для каждой координаты найдем максимальное число дифференцирований, при котором еще не появляется производная вектора 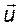 , то есть найдем такие числа
, то есть найдем такие числа  , что
, что
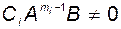 и
и 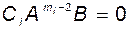 .
.
Таким образом, получим систему уравнений:
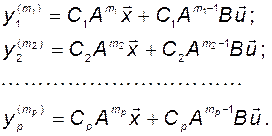 (3.10.5)
(3.10.5)
Запишем эту систему равенств в векторно-матричном виде:
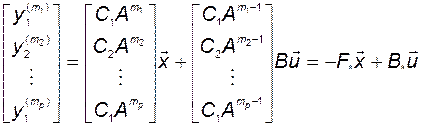 . (3.10.6)
. (3.10.6)
Обозначим
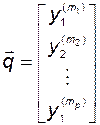 (3.10.7)
(3.10.7)
и
 ;
; 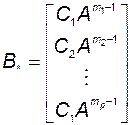 . (3.10.8)
. (3.10.8)
Тогда (3.10.6) можно переписать в виде
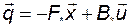 . (3.10.9)
. (3.10.9)
Если задача разделения каналов имеет решение, то матрица  не вырождена и
не вырождена и
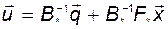 . (3.10.10)
. (3.10.10)
На рис. 3.10 представлена промежуточная структурная схема, соответствующая уравнениям (3.10.1), (3.10.2) и (3.10.8).

Для этой схемы справедливы уравнения
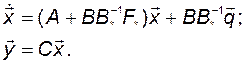 (3.10.11)
(3.10.11)
Обозначим
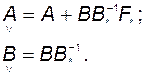 (3.10.12)
(3.10.12)
Теперь (3.10.11) превратится в
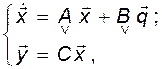 (3.10.13)
(3.10.13)
а структурная схема промежуточной системы с входным вектором 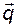 примет вид, представленный на рис. 3.11.
примет вид, представленный на рис. 3.11.
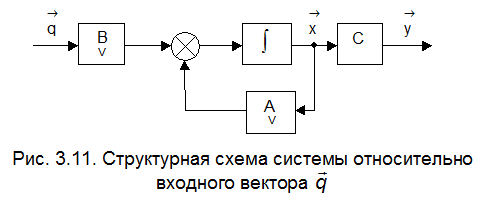
С другой стороны, вектор выхода  связан с вектором
связан с вектором 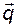 равенством (3.10.7), и поэтому схеме, представленной на рис. 3.11, полностью эквивалентна схема, составленная из
равенством (3.10.7), и поэтому схеме, представленной на рис. 3.11, полностью эквивалентна схема, составленная из  подсистем последовательно включённых интеграторов. Эта схема представлена на рис. 3.12.
подсистем последовательно включённых интеграторов. Эта схема представлена на рис. 3.12.
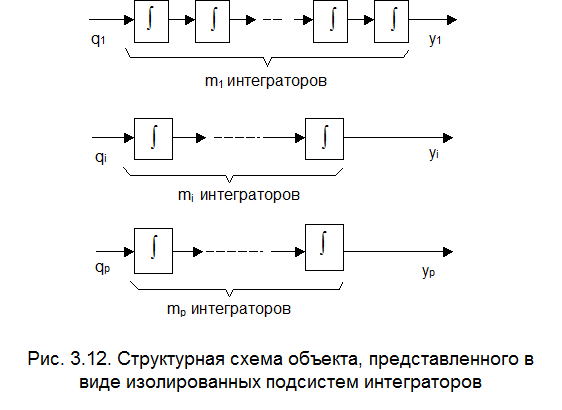
Общее количество интеграторов не может быть больше n, то есть
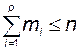 .
.
Таким образом, система 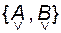 (3.10.13), у которой в качестве входного вектора выбран вектор
(3.10.13), у которой в качестве входного вектора выбран вектор 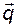 ,
,
а) развязана по каналам, то есть 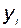 зависит только от
зависит только от 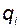 для всех значений
для всех значений 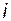 ;
;
б) имеет 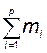 собственных значений, равных нулю.
собственных значений, равных нулю.
Теперь систему 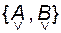 нужно попытаться привести к удобному базису, в котором следует синтезировать обратную связь, реализующую желаемые собственные числа по каждому каналу.
нужно попытаться привести к удобному базису, в котором следует синтезировать обратную связь, реализующую желаемые собственные числа по каждому каналу.
|
|
|
Прежде всего, установим некоторые свойства матриц  и
и 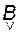 . Аналогично (3.10.4) запишем:
. Аналогично (3.10.4) запишем:
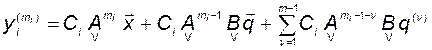 .
.
С другой стороны,  . Отсюда следует:
. Отсюда следует:
1) 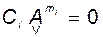 для всех i = 1,2,…, p; (3.10.14)
для всех i = 1,2,…, p; (3.10.14)
2) 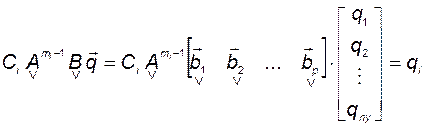 , (3.10.15)
, (3.10.15)
откуда
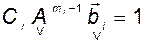 ; (3.10.16)
; (3.10.16)
 , при
, при 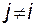 ; (3.10.17)
; (3.10.17)
3) 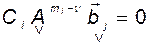 для
для  и для всех
и для всех 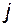 , i. (3.10.18)
, i. (3.10.18)
3.10.2. Преобразование базиса в пространстве 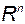
Перейдём от исходного базиса  к новому базису
к новому базису  с помощью некоторой матрицы преобразования
с помощью некоторой матрицы преобразования  . При выборе базиса
. При выборе базиса  учтем следующие обстоятельства:
учтем следующие обстоятельства:
§ объект управляем, поэтому ранг матрицы управляемости
 (3.10.19)
(3.10.19)
равен порядку системы;
§ так как каждый канал этой системы с размерностью  управляем, то столбцы
управляем, то столбцы
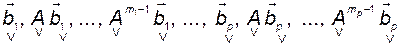
линейно независимы.
Теперь выберем базис  , соответствующий следующим координатным столбцам:
, соответствующий следующим координатным столбцам:
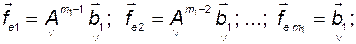
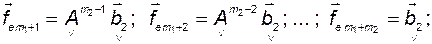 (3.10.20)
(3.10.20)
..................................
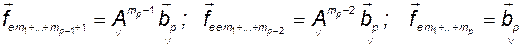 .
.
Если  , то оставшуюся часть векторов базиса
, то оставшуюся часть векторов базиса 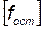 можно выбирать, перебирая оставшиеся столбцы матрицы
можно выбирать, перебирая оставшиеся столбцы матрицы 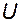 :
:

до тех пор, пока следующий вектор 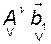 не будет выражаться в виде линейной комбинации всех предыдущих векторов базиса. Далее добавим
не будет выражаться в виде линейной комбинации всех предыдущих векторов базиса. Далее добавим  и так далее, пока число векторов базиса не достигнет числа
и так далее, пока число векторов базиса не достигнет числа 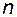 . Тогда матрица преобразования базиса
. Тогда матрица преобразования базиса  в базис
в базис  будет иметь вид
будет иметь вид
 .
.
Рассмотрим вид матрицы 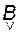 в базисе
в базисе  . Первый столбец этой матрицы, то есть вектор
. Первый столбец этой матрицы, то есть вектор 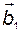 , совпадает с
, совпадает с 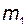 -м столбцом базиса
-м столбцом базиса  ; второй столбец матрицы
; второй столбец матрицы 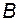 , то есть вектор
, то есть вектор 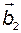 , совпадает с
, совпадает с  -м столбцом базиса
-м столбцом базиса  и так далее. Следовательно,
и так далее. Следовательно,
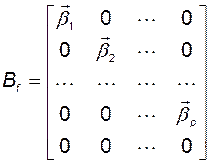 , (3.10.21)
, (3.10.21)
где
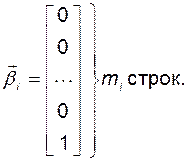 (3.10.22)
(3.10.22)
Теперь обратим внимание на матрицу  . В соответствии с (3.6.8)
. В соответствии с (3.6.8)
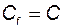

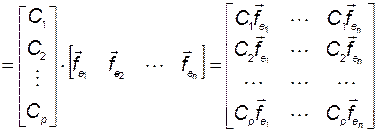 . (3.10.23)
. (3.10.23)
Из этого равенства с учётом (3.10.14), (3.10.16), (3.10.17) получим
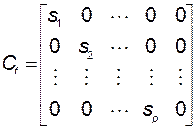 , (3.10.24)
, (3.10.24)
где
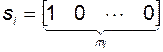 . (3.10.25)
. (3.10.25)
Наконец, займемся матрицей 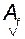 . Прежде всего, рассмотрим важную интерпретацию элементов матрицы
. Прежде всего, рассмотрим важную интерпретацию элементов матрицы  . В соответствии с (3.6.8)
. В соответствии с (3.6.8)

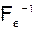

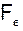 ,
,
поэтому
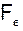


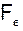 . (3.10.26)
. (3.10.26)
Левую часть этого равенства можно расписать следующим образом:
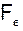

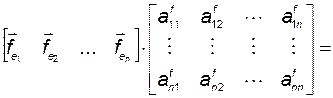
 .
.
С другой стороны:


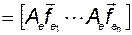 .
.
Таким образом, получаем
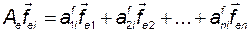 . (3.10.27)
. (3.10.27)
Это означает, что элементы 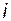 -го столбца матрицы
-го столбца матрицы 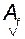
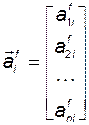
являются коэффициентами разложения произведения 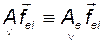 по координатным векторам
по координатным векторам 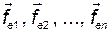 .
.
Используя (3.10.20), сопоставим произведения  с координатными столбцами векторов базиса
с координатными столбцами векторов базиса  :
:
 (3.10.28)
(3.10.28)
Так как векторы  ,
,  и т. д. не совпадают ни с одним из собственных векторов с номерами от 1 до
и т. д. не совпадают ни с одним из собственных векторов с номерами от 1 до 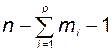 , то в соответствующих столбцах матрицы
, то в соответствующих столбцах матрицы 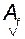 на позициях строк с номерами, большими
на позициях строк с номерами, большими  , могут находиться ненулевые элементы. Такие ячейки матрицы помечены символом "
, могут находиться ненулевые элементы. Такие ячейки матрицы помечены символом " 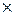 ". Кроме того, на данном этапе нет смысла рассматривать столбцы этой матрицы с номерами, большими
". Кроме того, на данном этапе нет смысла рассматривать столбцы этой матрицы с номерами, большими  . В результате получаем выражение для матрицы
. В результате получаем выражение для матрицы  в базисе
в базисе  :
:
|
|
|
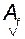 = =
| 0 1 0 … 0 0 0 1 … 0 …………. 0 0 0 … 1 0 0 0 … 0 | 0 0 0 … 0 0 0 0 … 0 …………. 0 0 0 … 0 0 0 0 … 0 | : : : : : | 0 0 0 … 0 0 0 0 … 0 …………. 0 0 0 … 0 0 0 0 … 0 |
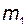
| |
| 0 0 0 … 0 0 0 0… 0 ………… 0 0 0 … 0 0 0 0 … 0 | 0 1 0 … 0 0 0 1 … 0 …………. 0 0 0 … 1 0 0 0 … 0 | : : : : : | 0 0 0 … 0 0 0 0 … 0 …………. 0 0 0 … 0 0 0 0 … 0 |
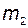
| ||
| …………. | …………. | …………. | ||||
| 0 0 0 … 0 0 0 0 … 0 …………. 0 0 0 … 0 0 0 0 … 0 | 0 0 0 … 0 0 0 0 … 0 …………. 0 0 0 … 0 0 0 0 … 0 | : : : : : | 0 1 0 … 0 0 0 1 … 0 …………. 0 0 0 … 1 0 0 0 … 0 |
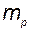
| ||
| * 0 0 … 0 …………. * 0 0 … 0 | * 0 0 … 0 …………. * 0 0 … 0 | : : : | * 0 0 … 0 …………. * 0 0 … 0 |

| ||
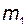
| 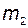
| 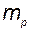
| 
|
Эту же матрицу удобнее записать в блочном виде:
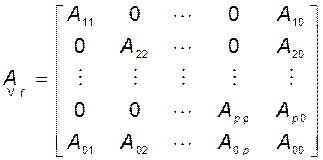 . (3.10.29)
. (3.10.29)
Разобьём вектор состояния 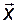 на систему
на систему  частных векторов и обозначим
частных векторов и обозначим
 , (3.10.30)
, (3.10.30)
где  имеет размерность
имеет размерность 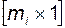 . Тогда уравнения (3.10.13) в базисе
. Тогда уравнения (3.10.13) в базисе  примут вид
примут вид

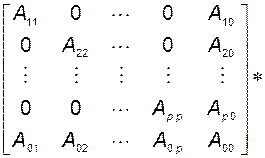
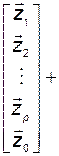
 ;
;
 . (3.10.31)
. (3.10.31)
Отсюда следуют уравнения для частных подсистем:
 ; (3.10.32)
; (3.10.32)
 ,
, 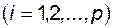 ;
;
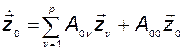 . (3.10.33)
. (3.10.33)
Раскроем систему дифференциальных уравнений для 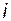 -й подсистемы:
-й подсистемы:
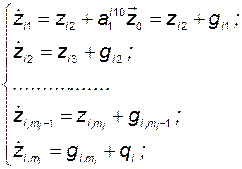 (3.10.34)
(3.10.34)
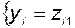 ,
,
где 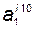 - первая строка матрицы
- первая строка матрицы 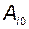 . Такой подсистеме соответствует структурная схема, представленная на рис. 3.13.
. Такой подсистеме соответствует структурная схема, представленная на рис. 3.13.
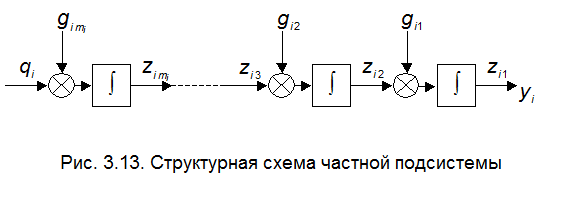
Из сопоставления этой схемы со схемой, приведённой на рис. 3.12, следует:
а) 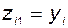 ;
; 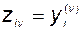 при
при  ;
;
б) 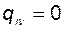 и
и 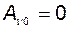 для
для 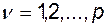 .
.
Таким образом, выходы интеграторов частных подсистем, показанных на рис. 3.12, совпали с координатами вектора 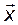 в базисе
в базисе  . Кроме того, все блочные матрицы
. Кроме того, все блочные матрицы 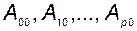 в (3.10.29)- нулевые.
в (3.10.29)- нулевые.
Работая в базисе  , мы имеем
, мы имеем  изолированных подсистем, сумма выходов которых подаётся на вход общей подсистемы с матрицей динамики
изолированных подсистем, сумма выходов которых подаётся на вход общей подсистемы с матрицей динамики 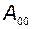 размерности
размерности 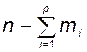 :
:
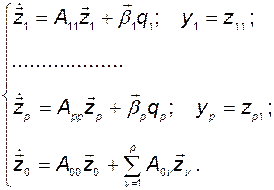 (3.10.35)
(3.10.35)
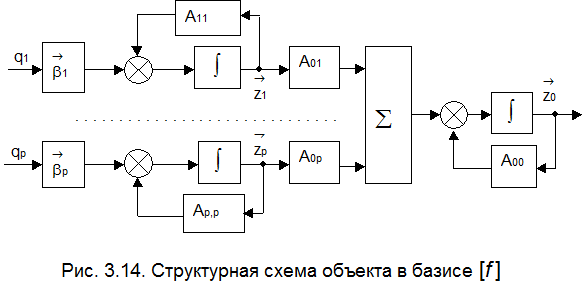
Соответствующая структурная схема представлена на рис. 3.14.
Пары матриц  для
для 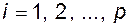 имеют форму УКП, причем каждая из матриц
имеют форму УКП, причем каждая из матриц 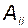 имеет только нулевые собственные значения. Это вполне согласуется с тем, что в п. 3.10.1 было произведено преобразование объекта на подсистемы последовательно включённых интеграторов. Сформируем управление
имеет только нулевые собственные значения. Это вполне согласуется с тем, что в п. 3.10.1 было произведено преобразование объекта на подсистемы последовательно включённых интеграторов. Сформируем управление  для
для 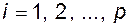 в следующем виде:
в следующем виде:
|
|
|
 , (3.10.36)
, (3.10.36)
где
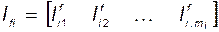 -
-
матрица обратной связи для 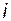 -й подсистемы в базисе
-й подсистемы в базисе  .
.
Тогда получим следующее дифференциальное уравнение для 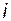 -й подсистемы:
-й подсистемы:
 ,
,
или
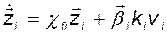 . (3.10.37)
. (3.10.37)
Нетрудно убедиться, что матрица динамики 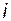 -й подсистемы в базисе
-й подсистемы в базисе  имеет вид
имеет вид
 . (3.10.38)
. (3.10.38)
Следовательно, определены характеристические полиномы подсистем:
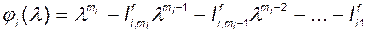 . (3.10.39)
. (3.10.39)
Согласно (3.8.22), а также с учетом (3.10.13), (3.10.24) и (3.10.37) запишем выражение для передаточной функции замкнутой 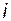 -й подсистемы:
-й подсистемы:
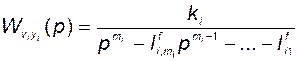 . (3.10.40)
. (3.10.40)
Очевидно
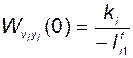 . (3.10.41)
. (3.10.41)
Задавая расположение полюсов и статику для каждой подсистемы, в итоге получим матрицы
 . (3.10.42)
. (3.10.42)
Возвращаясь в исходный базис для уравнений (3.10.13), получим
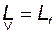
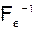 . (3.10.43)
. (3.10.43)
При этом вектор 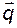 формируется в соответствии с выражением
формируется в соответствии с выражением
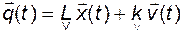 . (3.10.44)
. (3.10.44)
Учитывая (3.10.10), окончательно получим
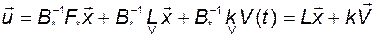 , (3.10.45)
, (3.10.45)
где
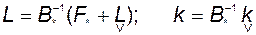 . (3.10.46)
. (3.10.46)
На этом можно закончить синтез, если часть системы, оказавшаяся вне обратной связи, имеет допустимые динамические свойства. Если же нет, например 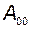 - неустойчива, то приходится идти на то, чтобы ввести обратную связь
- неустойчива, то приходится идти на то, чтобы ввести обратную связь  , по вектору
, по вектору 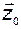 , по крайней мере, через один из каналов
, по крайней мере, через один из каналов 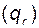 , оставив полностью развязанными остальные
, оставив полностью развязанными остальные 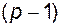 каналов. В этом случае
каналов. В этом случае  нужно рассчитывать совместно. Связь
нужно рассчитывать совместно. Связь  должна обеспечить «надзор» за бывшими ранее без контроля
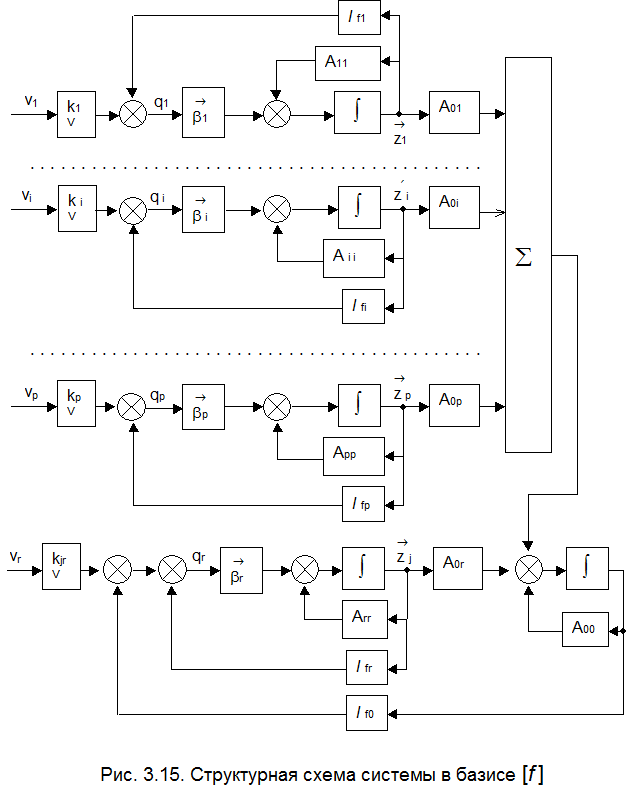
должна обеспечить «надзор» за бывшими ранее без контроля  полюсами (собственными числами) системы. Эта часть расчета может быть произведена по обычной методике синтеза системы с одним входом. Результирующая структура в базисе
полюсами (собственными числами) системы. Эта часть расчета может быть произведена по обычной методике синтеза системы с одним входом. Результирующая структура в базисе  приведена на рис. 3.15.
приведена на рис. 3.15.
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 625; Нарушение авторских прав?; Мы поможем в написании вашей работы!