Обратная связь по состоянию, обеспечивающая заданное (желаемое) расположение собственных чисел в замкнутой системе с одним (скалярным) входом

Передаточная функция и структура для системы в ИКП

В соответствии с видом матриц и уравнения системы со скалярным входом и скалярным выходом 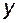имеют вид

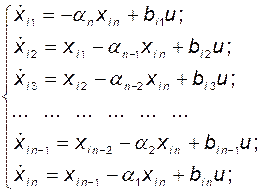(3.8.29)

. (3.8.30)

Этим уравнениям соответствует структурная схема, представле­нная на рис. 3.8.

В соответствии с этим рисунком передаточная функция системы имеет вид

(3.8.31)

Отметим, что статический передаточный коэффициент

. (3.8.32)

Даны уравнения полностью управляемого объекта управления в некотором исходном базисе

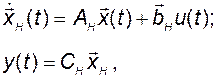(3.9.1)

каждая координата вектора состояния которого доступна для измерения.

Требуется синтезировать такое управление, которое бы обеспе­чило требуемое качество отработки внешнего командного сигнала .

Динамические свойства системы управления в основном определяются её собственными числами, то есть нулями характеристического полинома

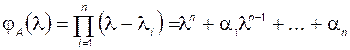. (3.9.2)

Время переходного процесса каждой моды определяется расстоянием до мнимой оси вещественной части; колебательность - соотношением мнимой и вещественной частей соответствующих собственных чисел. Эти зависимости могут быть проанализированы при изучении характеристик типовых звеньев, кроме того, они рассматриваются в обширной учебной литературе по теории автоматического регулирования и управления.

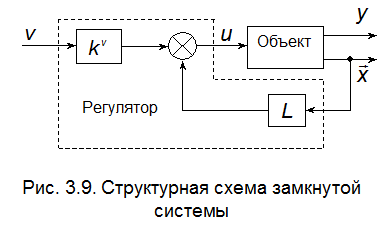
В соответствии со структурной схемой, приведённой на рис. 3.9, сформируем сигнал управления объектом в виде

, (3.9.3)

где – некоторая матрица-строка обратной связи:

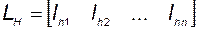; (3.9.4)

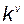– коэффициент по командному сигналу.

Тогда уравнение системы примет вид

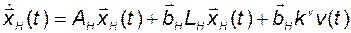, (3.9.5)

или

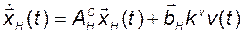, (3.9.6)

где - матрица замкнутой системы в исходном базисе:

. (3.9.7)

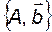Поскольку объект полностью управляем, то существует базис , в котором пара имеет управляемое каноническое представление . Поэтому перейдём к записи уравнений системы в базисе УКП. В соответствии с (3.4.16) произведём замену

. (3.9.8)

Тогда из (3.9.1) получим

; (3.9.9)

. (3.9.10)

Умножив уравнение (3.9.9) слева на , будем иметь

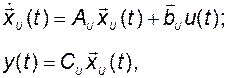(3.9.11)

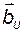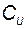где и - соответствующие матрицы в УКП.

Используя подстановку (3.9.8), из (3.9.3) получим

, (3.9.12)

где матрица обратной связи в базисе УКП

. (3.9.13)

В результате уравнение замкнутой системы в базисе управляемого канонического представле­ния будет иметь вид

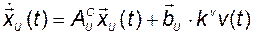. (3.9.14)

Здесь является сопровождающей матрицей по отношению к характеристическому полиному замкнутой системы

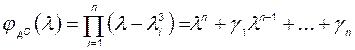, (3.9.15)

поэтому она имеет стандартный вид

. (3.9.16)

С другой стороны, очевидно, что

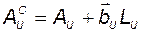. (3.9.17)

Отсюда сразу же следует связь между коэффициентами характеристического полинома (3.9.2) объекта и коэффициентами характеристического полинома (3.9.14) желаемой системы:

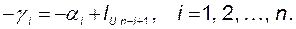(3.9.18)

Далее обусловлены следующие действия.

1) Задание желаемых собственных чисел замкнутой системы .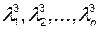

2) Вычисление коэффициентов характеристического полинома замкну­той системы 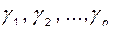в соответствии с выражением (3.9.14).

3) Вычисление согласно (3.9.17) коэффициентов матрицы обратной связи в базисе УКП:

. (3.9.19)

4) Вычисление в соответствии с (3.9.12) и (3.8.17) матрицы обратной связи в исходном базисе:

. (3.9.20)

5) Определение величины коэффициента 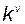в соответствии с требова­ниями по статике.

Так, например, если требуется обеспечить единичную статику по командному сигналу 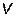, то это значит, что установившееся значение пе­реходной функции 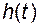замкнутой системы должно быть равно единице. Одним из свойств передаточной функции устойчивой системы является равенство

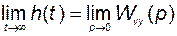. (3.9.21)

Согласно структурной схеме, приведённой на рис. 3.9, передаточная функция между командным 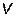и выходным 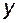сигналами имеет вид

, (3.9.22)

где передаточная функция 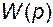может быть определена аналогично выражению (3.8.22). Таким образом, получаем

, (3.9.23)

откуда, окончательно,

. (3.9.24)

Дата добавления: 2015-03-31