
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Линейные операторы и матрицы линейных операторов
|
|
|
|
Отображение 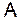 линейного пространства
линейного пространства  в линейное пространство
в линейное пространство 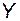
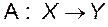
называют линейным преобразованием или линейным оператором, если оно удовлетворяет двум условиям:
а)
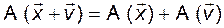 для всех
для всех 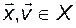 ; (3.5.1)
; (3.5.1)
б)
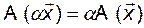 для всех
для всех 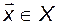 и любого
и любого 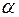 . (3.5.2)
. (3.5.2)
Если отображение 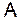 переводит вектор
переводит вектор 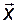 в некоторый другой вектор
в некоторый другой вектор  :
:
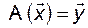 , (3.5.3)
, (3.5.3)
то вектор  называют образом вектора
называют образом вектора 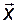 , а
, а 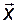 - прообразом вектора
- прообразом вектора  .
.
Линейный оператор, отображающий линейное пространство 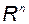 само в себя, называется линейным оператором в
само в себя, называется линейным оператором в 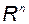 .
.
Пусть 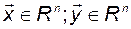 и
и 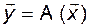 . Рассмотрим, как связаны в этом случае координаты векторов
. Рассмотрим, как связаны в этом случае координаты векторов 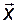 и
и  . Будем ориентироваться сначала на базис
. Будем ориентироваться сначала на базис 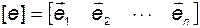 . Очевидно при этом, что
. Очевидно при этом, что
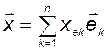 ; (3.5.4)
; (3.5.4)
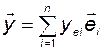 . (3.5.5)
. (3.5.5)
Рассмотрим прежде всего, как действует оператор 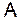 на элементы базиса. Пусть
на элементы базиса. Пусть
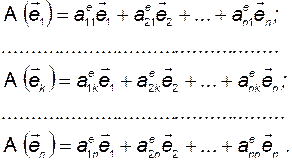 (3.5.6)
(3.5.6)
Из соотношений (3.5.3) и (3.5.4) следует
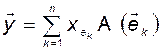 . (3.5.7)
. (3.5.7)
Учтём (3.5.6):
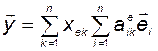 . (3.5.8)
. (3.5.8)
Сопоставляя это равенство с (3.5.5), получим
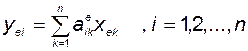 . (3.5.9)
. (3.5.9)
Запишем этот результат в матричной форме:
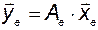 , (3.5.10)
, (3.5.10)
где, как и раньше, 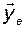 и
и 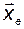 - координатные вектор-столбцы соответствующих векторов в базисе
- координатные вектор-столбцы соответствующих векторов в базисе  , а матрица
, а матрица
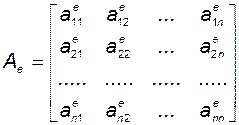 (3.5.11)
(3.5.11)
называется матрицей оператора 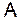 в базисе
в базисе  . Элементы её столбцов по построению - это координаты векторов
. Элементы её столбцов по построению - это координаты векторов 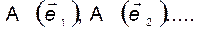 в базисе
в базисе  . Аналогично вводится понятие матрицы
. Аналогично вводится понятие матрицы 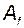 того же оператора
того же оператора 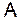 в некотором другом базисе
в некотором другом базисе  .
.
Рассмотрим теперь, как изменяется матрица оператора 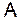 при замене базиса в пространстве
при замене базиса в пространстве 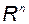 . Пусть, как и прежде,
. Пусть, как и прежде, 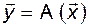 и матрица
и матрица  , в соответствии с (3.5.10), связывает между собой координатные столбцы векторов
, в соответствии с (3.5.10), связывает между собой координатные столбцы векторов 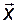 и
и  в базисе
в базисе  .
.
Согласно ранее полученным результатам - соотношениям (3.4.16),
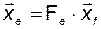 (3.5.12)
(3.5.12)
и
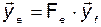 . (3.5.13)
. (3.5.13)
Из этих двух соотношений и (3.5.10) легко выводится равенство
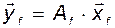 , (3.5.14)
, (3.5.14)
где
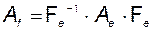 . (3.5.15)
. (3.5.15)
Эта формула позволяет связать между собой матрицы одного и того же оператора в различных базисах. В математике такие матрицы называются подобными. Ранее (п.2.4.3) уже отмечалось, что подобные матрицы имеют одинаковые собственные числа.
ПРИМЕР 3.5.1. Пусть имеется базис  (рис. 3.4).
(рис. 3.4).
1. Зададим оператор 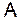 его действием на векторы базиса
его действием на векторы базиса  :
:
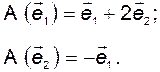
Тем самым мы определили матрицу оператора 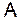 в базисе
в базисе  :
:
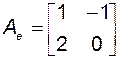 .
.
2. Зададим вектор 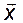 в базисе
в базисе  :
:
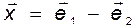 .
.

Отсюда
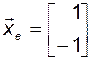 .
.
3. Рассчитаем координатный вектор, используя (3.5.14):
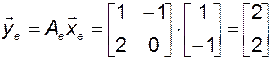 .
.
4. Введем новый базис  :
:
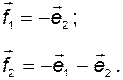
Тогда матрица перехода от базиса  к базису
к базису  будет иметь вид
будет иметь вид
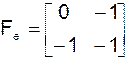 .
.
5. Определим матрицу 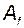 оператора
оператора 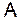 в базисе
в базисе  :
:
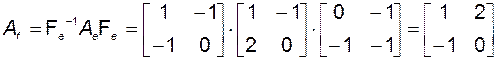 .
.
6. Найдём координатный столбец вектора 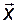 в базисе
в базисе  . В соответствии с рис. 3.4
. В соответствии с рис. 3.4
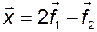 .
.
С другой стороны, согласно (3.5.12)
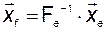 . (3.5.16)
. (3.5.16)
Оба подхода дают один и тот же результат:
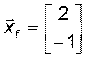 .
.
В итоге получим координатный столбец вектора  в базисе
в базисе  :
:
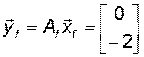 .
.
ПРИМЕР 3.5.2. Дана матрица  оператора
оператора 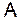 в базисе
в базисе  :
:
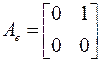
и два вектора - 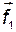 и
и 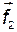 , координатные столбцы которых в том же базисе имеют вид
, координатные столбцы которых в том же базисе имеют вид
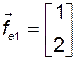 ;
; 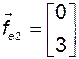 ,
,
то есть
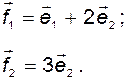
Примем эти векторы в качестве нового базиса и вычислим в нём матрицу 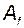 оператора
оператора 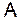 . Для этого выполним следующие действия.
. Для этого выполним следующие действия.
1. Составим матрицу перехода от базиса  к базису
к базису  :
:
 .
.
2. Вычислим обратную матрицу:
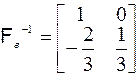 .
.
3. Вычислим матрицу 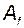 :
:
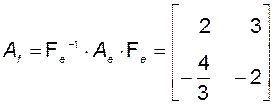 .
.
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 659; Нарушение авторских прав?; Мы поможем в написании вашей работы!