Управляемость линейных стационарных систем

Непрерывная линейная система

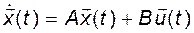(3.2.1)

является полностью управляемой тогда и только тогда, когда она может быть переведена из любого начального состояния 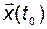в произвольный момент времени в любое конечное состояние 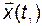за конечное время .

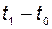Примем начальные условия нулевыми: 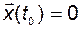. Тогда, в соответствии с формулой Коши,

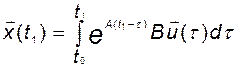. (3.2.2)

Принимая во внимание выражение для матричной экспоненты в виде бесконечного ряда

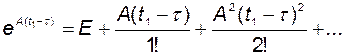, (3.2.3)

равенство (3.2.2) можно записать в виде

.

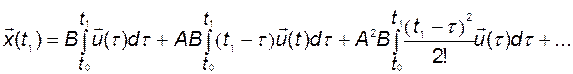Обозначим:

. (3.2.4)

Представим произведения 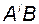в виде блочных матриц векторов :

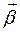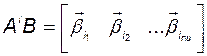. (3.2.5)

Тогда

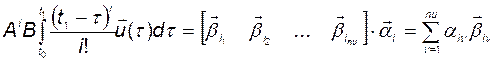(3.2.6)

и

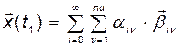. (3.2.7)

В результате вектор 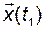может рассматриваться как линейная комбинация векторов 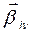, являющихся вектор-столбцами матриц 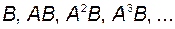. Иначе говоря, конечное состояние 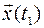принадлежит линейному подпространству, порождаемому вектор-столбцами бесконечной последовательности матриц .

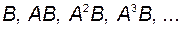В этой последовательности должна появиться матрица 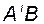, все вектор-столбцы которой линейно зависят от вектор-столбцов предыдущих матриц 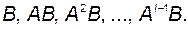Такая матрица обязательно должна иметь место, так как в линейном n- мерном пространстве не может быть более чем 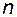линейно–независимых векторов. Отсюда же следует, что .

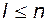Таким образом, можно записать

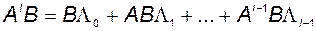, (3.2.8)

где 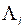- соответствующие диагональные матричные коэффициенты

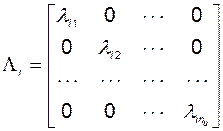. (3.2.9)

Очевидно, тем же свойством обладает и матрица 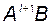, так как

. (3.2.10)

По индукции можно утверждать то же самое и для всех 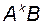при .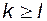

Итак, конечное состояние 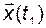принадлежит линейному подпространству, порождаемому вектор-столбцами матриц

...,

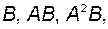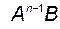
(здесь учтено, что 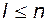). Если эти вектор-столбцы не порождают 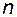-мерное пространство, то в такой системе можно достичь лишь тех состояний, которые принадлежат подпространству меньшей размерности.

Таким образом, критерий управляемости формулируется следующим образом:

Система 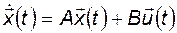полностью управляема тогда и только тогда, когда ранг матрицы управляемости

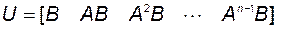(3.2.11)

равен 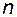, то есть полной размерности линейного пространства. При этом говорят, что пара матриц {A, B} полностью управляема.

ПРИМЕР 3.2.1. Определить управляемость системы

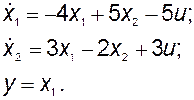
Для этой системы

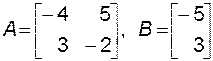
и матрица управляемости

.

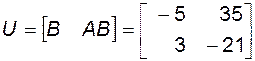Определитель этой матрицы равен нулю, она имеет ранг меньше двух, то есть порядка системы, и система является неуправляемой.

Отметим, что собственные числа матрицы динамики системы

,

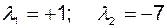то есть система неустойчива. В то же время передаточная функция по выходной координате

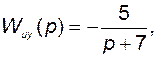
у неё только один - устойчивый полюс - и по ней не видно, что в действительности система неустойчива.

Матричная передаточная функция по вектору состояния

.

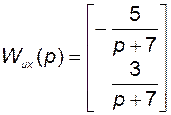Ей соответствует решение дифференциального уравнения системы

.

Как видно, в вынужденной составляющей решения отсутствует одна - неустойчивая - мода. Кроме того, независимо от управляющего сигнала для координат вынужденной составляющей вектора состояния существует линейная связь

.

ПРИМЕР 3.2.2. Определить управляемость системы

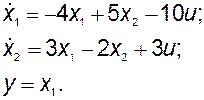
Для этой системы

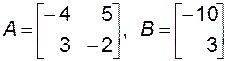
и матрица управляемости

.

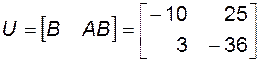Определитель этой матрицы не равен нулю, она имеет ранг, равный двум, то есть порядку системы, и система является полностью управляемой.

Отметим, что в данном случае полюсы передаточной функции

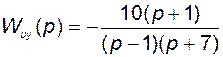
полностью повторяют все собственные числа матрицы .

Дата добавления: 2015-03-31