Интегральные критерии качества с позиций общности задач оптимального и модального синтеза

При рассмотрении качества систем управления большое место занимает группа интегральных критериев качества. Они достаточно полно изложены в обширной литературе по теории автоматического регулирования и управления. Это – интегралы от координат вектора состояния, вектора управления, ошибки регулирования. Интегральные показатели, или критерии качества, непосредственно выходят на синтез оптимального управления. При этом под оптимальностью понимается минимум какого-либо интегрального критерия. Наиболее простой из них – это интеграл от квадрата ошибки отработки командного сигнала на бесконечном интервале времени

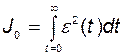. (2.11.1)

Однако, как показала практика, стремление к минимизации такого критерия приводит к чрезмерной колебательности переходных процессов. В связи с этим стали усложнять функционал. Так, например, кроме квадрата ошибки с целью уменьшения выбросов в переходных процессах в функционал стали вводить квадрат от её производной

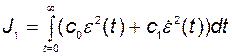. (2.11.2)

Кроме этого оказалось полезным учитывать величину управляющего воздействия:

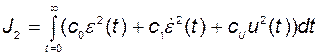. (2.11.3)

Различные исполнения системы в некоторых случаях стало удобным сравнивать по величине соответствующих интегральных показателей. Такой анализ неизбежно стал перерастать в синтез оптимального управления с различными интегральными критериями. В одной из наиболее общих форм интегральные критерии, используемые в оптимальном синтезе, записывают в виде

. (2.11.4)

Возникло целое направление в теории оптимальных систем – аналитическое конструирование регуляторов (АКР). Был разработан специальный математический аппарат, обеспечивающий расчёт управления, которое минимизирует функционал вида (2.11.4).

Однако возникла очередная проблема - проблема выбора значений элементов матриц 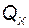, , 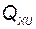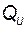в соответствующих квадратичных формах. Эту задачу в общем виде формализовать не удалось до сих пор. В то же время при проектировании систем выявилась важная закономерность: эталонные процессы, к которым притягивается движение в системе, должны соответствовать структуре управляемого объекта. Это означает, что уравнения эталонной системы, отображённой на рис. 2.46, должны иметь такой же вид, как и уравнения объекта. Поэтому в качестве эталонной системы можно выбрать систему того же порядка, что и объект, но с собственными числами, а значит, и с характеристическим полиномом, отвечающими требованиям, предъявляемым к замкнутой системе.

Рассмотрим способ формирования ошибки 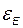, характеризующей отклонение некоторой конкретной системы от эталонной. Пусть эталонная система 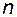однородных дифференциальных уравнений первого порядка приведена к одному дифференциальному уравнению 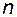-го порядка:

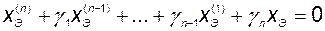. (2.11.5)

В левую часть равенства (2.11.5) вместо координаты 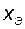подставим одну из координат вектора состояния объекта. Скорее всего при этом равенство нулю нарушится. Получаем уравнение невязки:

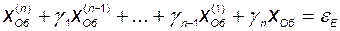. (2.11.6)

Переменная 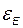характеризует отклонение процессов объекта от эталонных. Она равна нулю на интервале времени 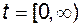только лишь в том случае, когда процессы в объекте или в проектируемой системе полностью тождественны процессам в эталонной системе.

Учтём уравнение объекта

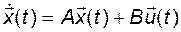(2.11.7)

и приведём уравнение (2.11.6) к такому виду, чтобы в него входили только координаты векторов состояния 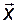и управления :

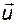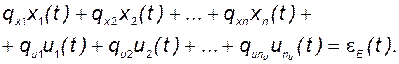(2.11.8)

Это уравнение, используя очевидные обозначения, можно записать иначе:

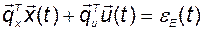. (2.11.9)

В соответствии с введённой текущей ошибкой 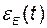может быть использован интегральный критерий качества (функционал)

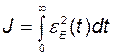. (2.11.10)

Квадрат ошибки можно записать с помощью квадратичных форм:

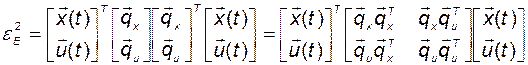, (2.11.11)

где

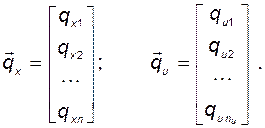(2.11.12)

Обозначив

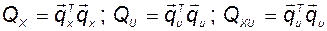, (2.11.13)

в итоге получаем критерий (2.11.4).

В связи с тем, что порядки уравнений объекта и эталонной системы совпадают, в результате оптимального синтеза удастся найти оптимальное управление, при котором минимум функционала окажется равным нулю. Так как при этом для процессов в системе с оптимальным управлением окажется выполнимым равенство (2.11.6) при 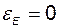, то полученная система будет иметь характеристический полином

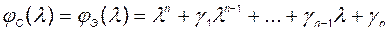(2.11.14)

и, следовательно, собственные числа синтезированной системы совпадут с собственными числами эталона.

Таким образом, результаты АКР при таком подходе обеспечивают не только минимум критерия (2.11.4), равный нулю, но и позволяет получить систему с желаемыми собственными числами. Поскольку связь переходных процессов с собственными числами (модами) системы более очевидна и непосредственна, модальный синтез часто оказывается предпочтительнее метода АКР, тем более, что алгоритм модального синтеза существенно проще алгоритмов АКР.

ПРИМЕР 2.11.1. Для иллюстрации изложенного рассмотрим объект, представленный на рис. 2.9. Уравнения объекта имеют следующий вид:

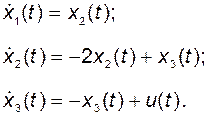(2.11.15)

Пусть эталонная система (эталонный процесс) определяется уравнением

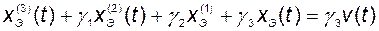, (2.11.16)

соответствующим желаемым собственным числам. Из этого уравнения видно, что при постоянном командном сигнале 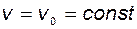в статике

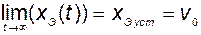. (2.11.17)

Подставив в левую часть равенства (2.11.16) координату объекта 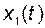, получим уравнение невязки:

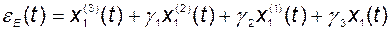. (2.11.18)

Заменим производные от координаты 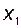на координаты вектора состояния объекта с учётом уравнений (2.11.15):

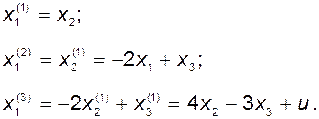(2.11.19)

В результате уравнение невязки принимает вид

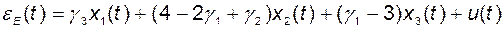, (2.11.20)

откуда получаем

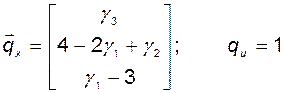. (2.11.21)

Теперь в соответствии с (2.11.13) могут быть вычислены матрицы 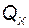, , 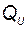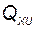и получен функционал (2.11.4) для использования при решении задачи АКР.

В то же время, приравняв нулю 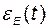в (2.11.20), можно непосредственно получить выражение для формирования управления 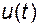через координаты вектора состояния объекта. Более того, если потребовать выполнения равенства

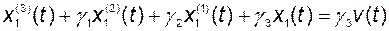, (2.11.22)

то с учётом (2.11.20) получим систему с обратной связью по вектору состояния и управлением

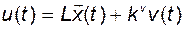, (2.11.23)

где фигурируют матрица обратной связи

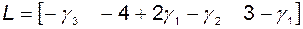(2.11.24)

и передаточный коэффициент по командному сигналу

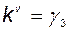. (2.11.25)

Таким образом, без решения задачи АКР получено оптимальное управление, обеспечивающее процессы в замкнутой системе, имеющей собственные числа, соответствующие характеристическому полиному эталонной системы (2.11.14). Кроме того, в полученной системе обеспечена единичная статика по командному сигналу 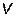(2.11.17).

В этом примере проиллюстрирована идентичность задачи АКР с надлежащим образом выбранным критерием оптимальности задаче модального синтеза. В следующих разделах будет подробно изложена методика модального синтеза.

Дата добавления: 2015-03-31