Наблюдаемость линейных стационарных систем

В теории автоматического управления большую роль играет задача восстановления вектора состояния по результатам наблюдения за входом и выходом объекта.

Непрерывная система

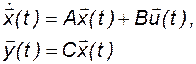(3.3.1)

называется наблюдаемой, если вектор состояния 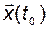можно определить, зная 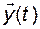на некотором интервале времени 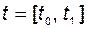. Если это справедливо для любого , то система называется полностью наблюдаемой. Задачей настоящего параграфа является вывод критерия наблюдаемости.

Достаточно рассмотреть задачу при . Тогда

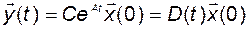. (3.3.2)

В развёрнутом виде - это система алгебраических уравнений

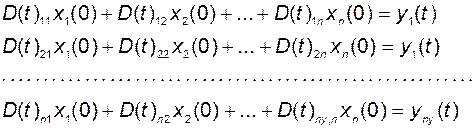, (3.3.3)

в качестве неизвестных в которой выступают координаты вектора состояния. В связи с тем, что, как правило, , число уравнений оказывается меньше числа неизвестных, и решение невозможно.

В соответствии с теоремой Кэли-Гамильтона каждая квадратная матрица удовлетворяет собственному характеристическому уравнению:

. (3.3.4)

Поэтому матричная экспонента, являющаяся степенным рядом относительно матрицы , может быть представлена в виде полинома степени 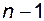. С учетом этого равенство (3.3.2) можно записать в виде

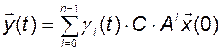, (3.3.5)

где 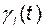– соответствующие коэффициенты этого полинома. Для i-й составляющей вектора выхода соответственно будем иметь

. (3.3.6)

Здесь – 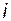-я строка матрицы .

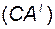Если набор для 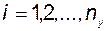; 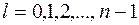не содержит полного базиса, то есть 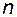линейно независимых строк, иначе говоря, если матрица

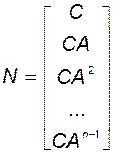(3.3.7)

имеет ранг, меньший, чем 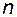, то в качестве ненулевого вектора начальных условий 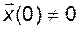может быть выбран вектор, ортогональный всем строкам матрицы N. Тогда в соответствии с (3.3.5) получим, что для всех , т.е. система не наблюдаема.

Теперь докажем, что если ранг матрицы N равен 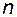, то может быть определен с помощью конечного числа измерений вектора выхода 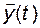. Обозначим

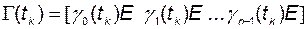, (3.3.8)

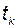где Е – квадратная единичная матрица размером . Моменты измерения выберем таким образом, чтобы для различных значений элементы отличались друг от друга. С учетом введенного обозначения равенство (3.3.5) примет вид

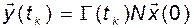. (3.3.9)

Известно, что ранг произведения любых двух матриц не превосходит ранга каждого из сомножителей. Ранг матрицы 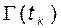не превосходит числа ее строк . Проводя многократные измерения на интервале времени переходного процесса системы, построим расширенный вектор выхода

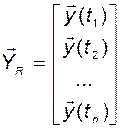(3.3.10)

и обозначим

. (3.3.11)

Матрица 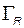имеет 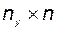строк. Моменты измерений должны быть выбраны таким образом, чтобы выполнялось условие 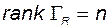. Как было обусловлено, ранг матрицы также равен 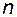. Поэтому уравнение

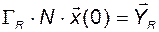(3.3.12)

содержит 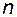линейно независимых скалярных уравнений, то есть оно может быть разрешено относительно вектора .

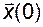Таким образом, доказан следующий критерий полной наблюдаемости стационарных линейных систем:

Линейная стационарная система вполне наблюдаема тогда и только тогда, когда ранг матрицы наблюдаемости N равен .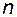

ПРИМЕР 3.3.1. Объект управления задан уравнениями

Этим уравнениям соответствуют матрицы

.

Определитель матрицы управляемости

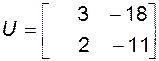
не равен нулю, поэтому система управляема. Матрица наблюдаемости

.

Её определитель также отличен от нуля, следовательно, система полностью наблюдаема.

Для данного объекта нетрудно рассчитать собственные числа

,

правые

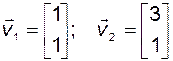
и левые

;

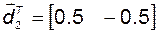
собственные векторы.

В соответствии с (2.4.27), (2.6.4) и (2.6.6) нетрудно получить передаточные функции по векторам состояния и выхода:

;

.

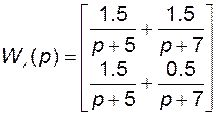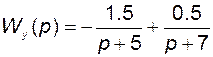В данном случае полюсы передаточной функции по выходу полностью отображают собственные числа матрицы динамики.

ПРИМЕР 3.3.2. Объект управления задан уравнениями

; .

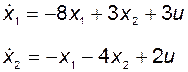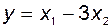Матрицы и 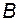здесь такие же, как и в предыдущем примере, следовательно, объект управляем. Матрица выхода

.

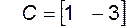Ранг матрицы наблюдаемости

в данном случае меньше порядка объекта и равен единице, так как второй столбец пропорционален первому. Следовательно, данный объект неуправляем.

Правые и левые собственные векторы матрицы динамики и передаточная функция по вектору состояния такие же, как и в предыдущем примере. Передаточная функция по выходу

.

У неё отсутствует полюс, равный второму собственному числу матрицы .

Определим свободное движение объекта по вектору состояния и по выходу:

Получаем:

;

.

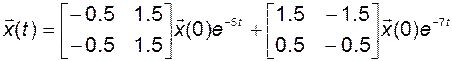Если выбрать

,

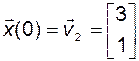то, так как векторы 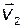и взаимно ортогональны и их скалярное произведение равно нулю, получим

,

в то время как

.

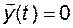Дата добавления: 2015-03-31