
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Канонические представления систем
|
|
|
|
3.8.1.Управляемое каноническое представление системы
со скалярным входом
Пусть в некотором исходном базисе 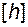 пространства состояний
пространства состояний  записаны уравнения движения объекта со скалярным управлением:
записаны уравнения движения объекта со скалярным управлением:
 ; (3.8.1)
; (3.8.1)
 . (3.8.2)
. (3.8.2)
Более общая запись связывает не координатные столбцы, а сами векторы в 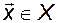 с помощью соответствующего оператора
с помощью соответствующего оператора 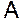 :
:
 . (3.8.3)
. (3.8.3)
Если система  управляема, то n векторов
управляема, то n векторов 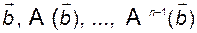 образуют базис в пространстве X в силу того, что
образуют базис в пространстве X в силу того, что 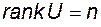 . Следовательно, в пространстве X в качестве базиса может быть выбрана следующая система векторов:
. Следовательно, в пространстве X в качестве базиса может быть выбрана следующая система векторов:
 (3.8.4)
(3.8.4)
Пусть характеристический полином оператора 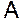 , а значит, и его матрицы в преобразованном базисе имеет вид:
, а значит, и его матрицы в преобразованном базисе имеет вид:
 . (3.8.5)
. (3.8.5)
Построим ещё один базис - базис  следующим образом:
следующим образом:
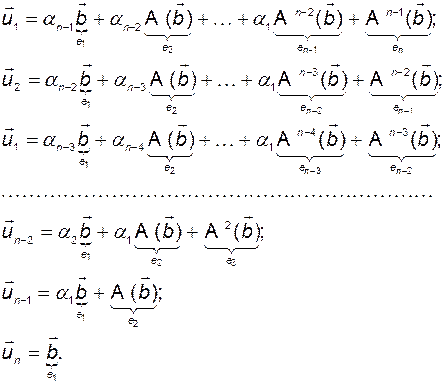 (3.8.6)
(3.8.6)
Проверим, действительно ли это базис? Матрица перехода от базиса  к базису
к базису  в соответствии с (3.4.4) и (3.4.5) имеет вид
в соответствии с (3.4.4) и (3.4.5) имеет вид
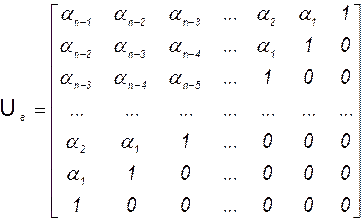 . (3.8.7)
. (3.8.7)
Эта матрица является треугольной, её определитель равен произведению диагональных элементов, умноженному на 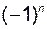 , т.е. не равен нулю. Следовательно,
, т.е. не равен нулю. Следовательно, 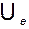 не вырождена и система векторов
не вырождена и система векторов 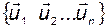 действительно образует базис в пространстве X.
действительно образует базис в пространстве X.
Вычислим теперь представление матрицы оператора 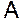 в базисе
в базисе  . При этом воспользуемся равенством
. При этом воспользуемся равенством
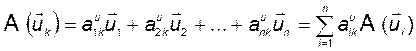 . (3.8.8)
. (3.8.8)
С учётом (3.8.6)
 (3.8.9)
(3.8.9)
По теореме Кэлли-Гамильтона 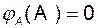 , а значит,
, а значит,  , откуда следует, что
, откуда следует, что  и
и  при
при 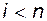 , то есть
, то есть
 . (3.8.10)
. (3.8.10)
Далее действуем аналогичным образом:
 , (3.8.11)
, (3.8.11)
откуда следует, что 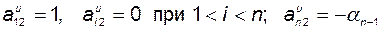 , то есть
, то есть
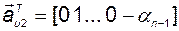 .
.
Далее:
 , (3.8.12)
, (3.8.12)
откуда следует, что
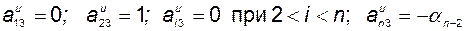 ,
,
то есть
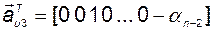 .
.
Вычислим предпоследний столбец матрицы:
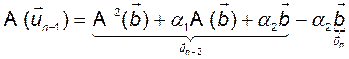 , (3.8.13)
, (3.8.13)
откуда следует, что 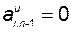 для
для 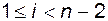 ,
, 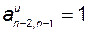 ,
, 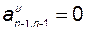 и
и 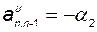 , то есть
, то есть
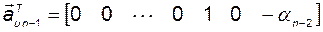 .
.
Наконец,
 , (3.8.14)
, (3.8.14)
откуда следует, что 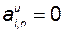 для
для 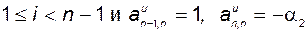 ,
,
то есть
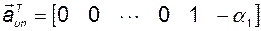 .
.
Таким образом, матрица  оператора
оператора 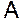 в базисе
в базисе  имеет вид
имеет вид
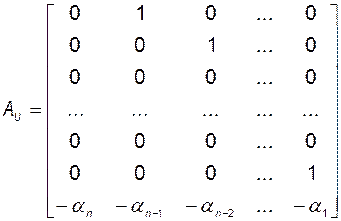 . (3.8.15)
. (3.8.15)
Так как  , то есть является последним вектором базиса
, то есть является последним вектором базиса  , то координатный столбец вектора
, то координатный столбец вектора  в этом базисе
в этом базисе
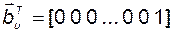 . (3.8.16)
. (3.8.16)
Пара 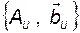 называется управляемым каноническим представлением (УКП) системы с одним (скалярным) входом. Матрица
называется управляемым каноническим представлением (УКП) системы с одним (скалярным) входом. Матрица  называется сопровождающей по отношению к полиному
называется сопровождающей по отношению к полиному 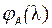 .
.
Таким образом, мы доказали, что если исходная система управляема, то в пространстве состояний Х существует базис, в котором пара 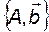 имеет управляемое каноническое представление.
имеет управляемое каноническое представление.
Если в некотором исходном базисе 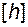 заданы матрицы
заданы матрицы 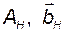 и если система управляема, то для того, чтобы вычислить их (матриц) УКП, достаточно вычислить коэффициенты характеристического полинома
и если система управляема, то для того, чтобы вычислить их (матриц) УКП, достаточно вычислить коэффициенты характеристического полинома 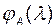 . После этого может быть вычислена матрица преобразования от исходного базиса
. После этого может быть вычислена матрица преобразования от исходного базиса 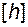 к УКП в соответствии с (3.7.8):
к УКП в соответствии с (3.7.8):
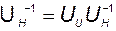 . (3.8.17)
. (3.8.17)
Далее индекс “h” для системы в исходном базисе будем опускать.
ПРИМЕР 3.8.1. Для системы

известны матрицы
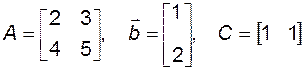 .
.
Нетрудно вычислить матрицу
 .
.
Её определитель  , откуда следует, что система управляема и, значит, для неё существует УКП. Вычислим характеристический полином:
, откуда следует, что система управляема и, значит, для неё существует УКП. Вычислим характеристический полином:
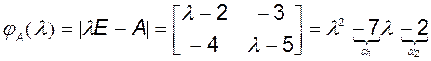 .
.
Это позволяет сразу же записать матрицы A и B в базисе УКП:
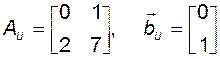 .
.
Векторно-матричные уравнения системы в УКП имеют вид
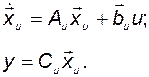
Для того чтобы найти матрицу 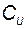 , требуется рассчитать матрицу перехода от исходного базиса к базису УКП. Для этого предварительно вычислим
, требуется рассчитать матрицу перехода от исходного базиса к базису УКП. Для этого предварительно вычислим
 и
и 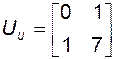 .
.
Тогда искомая матрица
 ,
,  .
.
После этого в соответствии с (3.6.8) находим
 .
.
3.8.2.Передаточная функция и структурная схема для системы
в УКП
Уравнения системы
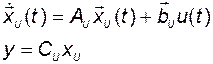 (3.8.18)
(3.8.18)
со скалярным входом 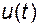 и скалярным выходом
и скалярным выходом  , где матрицы
, где матрицы  и
и 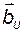 определяются выражениями (3.8.15) и (3.8.16), а матрица
определяются выражениями (3.8.15) и (3.8.16), а матрица 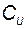 имеет вид
имеет вид
 , (3.8.19)
, (3.8.19)
можно записать в развёрнутом виде:
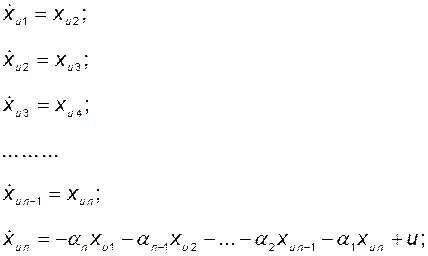 (3.8.20)
(3.8.20)
 . (3.8.21)
. (3.8.21)
Этим уравнениям соответствует схема, представленная на рис.3.7.
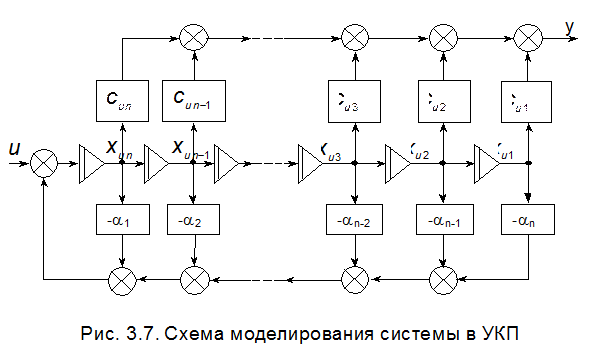
В соответствии с этим рисунком передаточная функция системы имеет вид
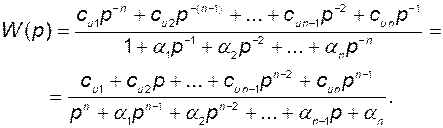 (3.8.22)
(3.8.22)
Отметим, что статический передаточный коэффициент
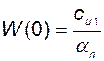 . (3.8.23)
. (3.8.23)
3.8.3.Идентификационное каноническое представление системы
с одним (скалярным) выходом
С помощью рассуждений, аналогичных проведённым в п.3.8.1, можно получить следующие результаты.
Если пара матриц  полностью наблюдаема, то в пространстве состояний Х всегда существует базис, в котором пара
полностью наблюдаема, то в пространстве состояний Х всегда существует базис, в котором пара  имеет идентификационное каноническое представление (ИКП):
имеет идентификационное каноническое представление (ИКП):
 ; (3.8.24)
; (3.8.24)
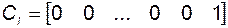 . (3.8.25)
. (3.8.25)
Отметим, что
 . (3.8.26)
. (3.8.26)
Если в некотором исходном базисе 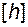 заданы матрицы
заданы матрицы 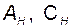 и если система полностью наблюдаема, то, для того чтобы вычислить их (матриц) ИКП, достаточно вычислить коэффициенты характеристического полинома
и если система полностью наблюдаема, то, для того чтобы вычислить их (матриц) ИКП, достаточно вычислить коэффициенты характеристического полинома 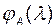 . После этого может быть вычислена матрица преобразования от исходного базиса
. После этого может быть вычислена матрица преобразования от исходного базиса 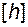 к ИКП в соответствии с (3.7.13):
к ИКП в соответствии с (3.7.13):
 . (3.8.27)
. (3.8.27)
Если известна матрица 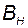 при векторе управления в исходном базисе, то с учётом (3.6.8) в базисе ИКП она может быть определена с помощью соотношения
при векторе управления в исходном базисе, то с учётом (3.6.8) в базисе ИКП она может быть определена с помощью соотношения
 . (3.8.28)
. (3.8.28)
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 1520; Нарушение авторских прав?; Мы поможем в написании вашей работы!