Замена базиса в пространстве состояний динамической системы

Пусть заданы уравнения системы

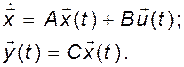(3.6.1)

Для этой системы могут быть найдены матрицы:

управляемости

, (3.6.2)

наблюдаемости

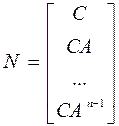, (3.6.3)

передаточной функции

. (3.6.4)

Могут быть также записаны выражения для векторов состояния и выхода

(3.6.5)

Полученные в предыдущих разделах результаты не были ограничены выбором какого-либо конкретного базиса в пространстве состояний. Все они были справедливы для любого базиса, в котором записаны матрицы . Для определённости назовём этот базис базисом . В этом случае можно подразумевать, что символы всех векторов и матриц в выражениях (3.6.1) - (3.6.5) снабжены индексом " 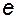". В дальнейшем нам будет удобно выбирать вполне определенный базис в пространстве состояний таким образом, чтобы матрицы имели «хорошую», каноническую форму. Такой выбор базиса может оказаться целесообразным, так как, во-первых, канонические представления матриц системы имеют минимальное число ненулевых элементов и поэтому удобны для моделирования и других вычислений, а во-вторых, канонические представления позволяют получить чрезвычайно простые алгоритмы синтеза управления.

Рассмотрим перевод уравнений (3.6.1) в некоторый новый базис . Отметим при этом, что, переходя к новому базису в пространстве состояний, преобразовывая базис для пространства вектора состояний, не будем изменять базис пространства входов и пространства выходов системы. Заменим в (3.6.1) 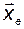на согласно (3.5.12):

(3.6.6)

Умножая слева обе части дифференциального уравнения на , получим

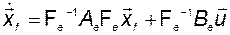. (3.6.7)

Учитывая (3.5.15) и вводя дополнительные обозначения

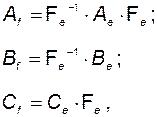(3.6.8)

окончательно получаем уравнения системы в базисе :

(3.6.9)

ПРИМЕР 3.6.1. Пусть система задана схемой моделирования, приведенной на рис. 3.5. Выберем в качестве координат вектора состояний в исходном базисе выходы интеграторов 1 и 2. В результате получим уравнения системы в исходном базисе:

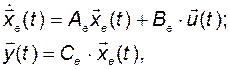
где

; ; .

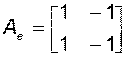Зададим матрицу перехода к новому базису

,

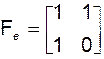которой соответствуют уравнения

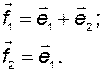
Вычислим обратную матрицу

.

В соответствии с (3.6.8) находим

; .

Этим матрицам соответствуют уравнения

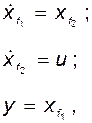
которым, в свою очередь, отвечает схема, приведённая на рис. 3.6.

Собственные числа системы, естественно, сохранились, так как матрицы и подобны. Связь между входом и выходом осталась неизменной, а схема моделирования стала заметно проще.

2.16.Вычисление матрицы преобразования базиса в пространстве состояний динамической системы
с помощью матриц управляемости и наблюдаемости

Пусть матрицы управляемой системы представлены в двух различных базисах и в пространстве состояний вектора :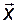

.

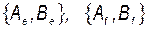Рассмотрим матрицу управляемости

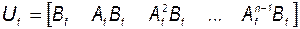. (3.7.1)

В соответствии с (3.6.8)

;

;

………….

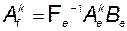. (3.7.2)

Учитывая эти равенства в (3.7.1), получим выражение для перевода матрицы управляемости из одного базиса в другой:

. (3.7.3)

Умножая это равенство справа на 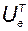, получаем

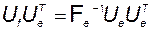. (3.7.4)

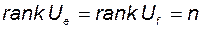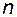Если система управляема, то . Это значит, что матрица имеет линейно независимых строк и может быть представлена в виде

, (3.7.5)

где векторы 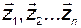– линейно независимы. Следовательно, матрица

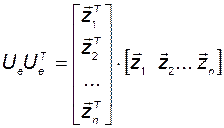, (3.7.6)

которая является матрицей Грама, имеет положительный определитель, а значит, – невырождена. Следовательно,

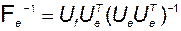. (3.7.7)

Если система имеет скалярный вход (u -скаляр), то матрица 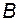ста­новится вектором , а матрица 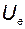– квадратной, в управляемой системе – невырожденной. Тогда

. (3.7.8)

Отметим, что в данном рассуждении – матрица перехода от базиса к базису , поэтому обратная ей - это матрица перехода от базиса к базису :

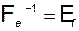. (3.7.9)

Рассмотрим другой случай, когда переход от базиса к базису задан парой матриц

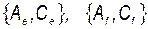
некоторой наблюдаемой системы. Запишем матрицу наблюдаемости (3.3.7) и с учётом (3.6.8) проведём аналогичные предыдущим преобразования:

. (3.7.10)

Так как система наблюдаема, то

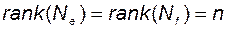
и матрица наблюдаемости имеет 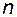линейно независимых столбцов

,

а квадратная матрица

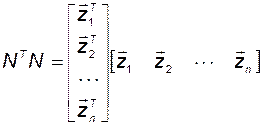
не вырождена. Умножим обе части равенства (3.7.10) слева на :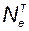

, (3.7.11)

откуда получим

. (3.7.12)

Если система имеет скалярный выход, то

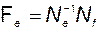. (3.7.13)

Дата добавления: 2015-03-31