Теорема 2.1

Якщо поверхню, задану рівнянням

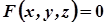, (1)

перетнути площиною 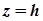, паралельною до площини , то в перерізі утвориться лінія, проекція якої на площину у напрямку осі 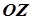в системі координат задається рівнянням

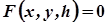. (2)

Доведення

Нехай деяку поверхню 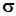перетнули площиною 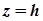і в перерізі отримали лінію (рис. 7.2). – проекція лінії на площину у напрямку осі 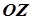. Покажемо, що рівняння (2) є рівнянням лінії у площині .

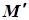Нехай належить лінії . Точка є проекцією деякої точки 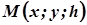, що належить лінії . Оскільки ця точка М належить даній поверхні, то її координати задовольняють рівняння поверхні (1), тобто 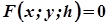. Таким чином, координати довільної точки 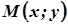кривої задовольняють рівняння (2).

Нехай тепер точка 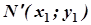площини не належить лінії . Ця точка є проекцією деякої точки 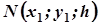, яка лежить у площині 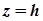, але не належить лінії . Отже, ця точка не лежить і на поверхні 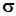. Тому .

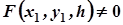Таким чином, рівняння (2) задовольняють координати точок кривої і тільки вони. Тому рівняння (2) є рівнянням кривої , що і треба було довести.

Аналогічно, якщо поверхню (1) перетнути площиною 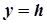, паралельною до площини 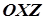, то рівняння проекції лінії перетину у напрямку 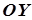на площину 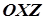у цій площині матиме рівняння .

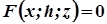Якщо ж поверхню (1) перетнути площиною 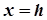, паралельною до 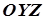, то рівняння проекції лінії перетину у напрямку осі ОX на площину ОYZ матиме вигляд .

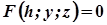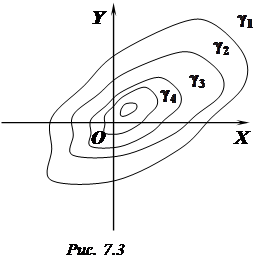Ця теорема дозволяє будувати карту перерізів поверхні на ту чи іншу координатну площину. Якщо, наприклад, поверхню перетнути площинами 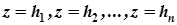, паралельними до площини і відповідні лінії перерізів спроектувати на площину , то на площині дістанемо карту відповідних перерізів, рівняння яких будуть 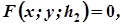…, 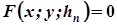(рис. 7.3).

Ця карта перерізів є сукупністю кривих, за формою і розміщенням яких можна судити про форму поверхні.

§ 3. Поверхні обертання

Означення 3.1

Нехай у деякій площині лежить пряма 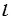і крива . Поверхня, яка утворюється внаслідок обертання кривої навколо прямої 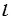, називається поверхнею обертання (рис. 7.4).

При цьому пряма 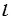називається віссю обер­тан­ня, а кри­­ва – твірною або меридіаном поверхні обертання. Кожна точка М кривої при цьому обертається по колу, площина якого перпендикулярна до осі 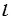, а центр знаходиться на осі 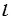. Це коло називається паралеллю поверхні обертання.

Складемо рівняння поверхні обертання.

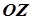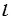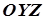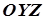Виберемо прямокутну систему координат так, щоб вісь збігалася з віссю обертання , а лінія , яка обертається, була розміщена в площині (рис. 7.5). Нехай крива у системі координат задається рівнянням

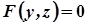, (1)

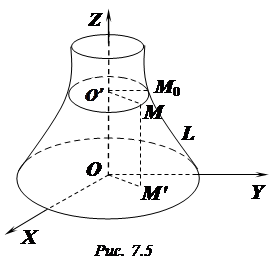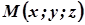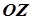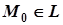а точка – довільна точка поверхні обертання. Через цю точку проведемо площину, перпендикулярну до осі . Вона перетне поверхню по колу, яке є паралеллю даної поверхні обертання. Припустимо, що це коло перетинається з лінією в точці . Оскільки точка , то її координати задовольняють рівняння (1):

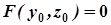. (2)

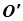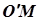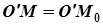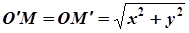Центр цього кола позначимо . – радіус паралелі, тому . Але якщо точку М спроектувати на площину , то її проекцією буде точка і , а . Звідси випливає, що , або 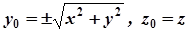. Підставивши одержані формули в (2), отримаємо

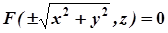. (3)

Отже, координати довільної точки М поверхні обертання задовольняють рівняння (3).

Припустимо тепер, що координати деякої точки 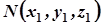задовольняють рівняння (3), тобто

. (4)

Покажемо, що ця точка належить даній поверхні обертання. Проведемо через точку N площину, перпендикулярну до осі 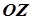(рис. 7.6).

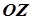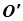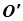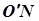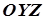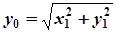Припустимо, що ця площина перетинає вісь в точці . Побудуємо в цій площині коло з центром радіусом . Нехай це коло перетинає площину в точці . Тоді . Звідси випливає, що , якщо 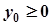, і 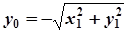, якщо 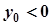. Крім того, оскільки точки 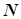і лежать у площині, паралельній до площини , то 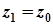. Тоді рівність (4) запишеться так: , звідки випливає, що точка належить меридіану, а це означає, що точка 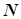лежить на даній поверхні обертання.

Отже, рівняння (3) – рівняння поверхні обертання.

Аналогічно можна встановити, що коли крива задана рівнянням 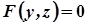у площині 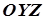і обертається навколо осі ОY, то рівняння поверхні обертання матиме вигляд

.

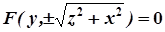Якщо крива знаходиться у площині 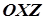, задана рівнянням і обертається навколо осі ОХ, то рівняння поверхні обертання

.

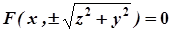В результаті приходимо до такого правила складання рівняння поверхні обертання: щоб скласти рівняння поверхні обертання, необхідно в рівнянні лінії, яка обертається, залишити без змін ту змінну, яка відповідає осі обертання, а другу змінну замінити на корінь квадратний, взятий із знаками “+” та “–“, з суми квадратів цієї ж змінної і тієї змінної, яка відсутня в рівнянні кривої.

Дата добавления: 2015-03-31