Приклад. При перетині еліпсоїда довільною площиною в перерізі утворюється еліпс

Т е о р е м а 6.1

При перетині еліпсоїда довільною площиною в перерізі утворюється еліпс.

Доведення

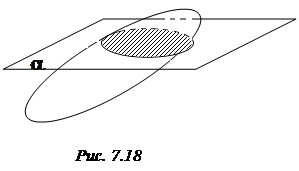Оскільки еліпсоїд є обмеженою поверхнею, то при перетині його з будь-якою площиною утвориться обмежена крива другого порядку (див. теорему 1.1 §1). Тому ця крива не може бути ні параболою, ні гіперболою, ні парою прямих. Отже, вона є еліпсом, що й треба було довести (рис. 7.18).

Записати рівняння еліпсоїда, осі якого збігаються з осями координат, і який проходить через точку 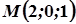та перетинає площину по еліпсу

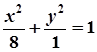. (2)

Розв’язання

Якщо осі координат збігаються з осями еліпсоїда, то ця система координат є канонічною, тому рівняння еліпсоїда матиме вигляд:

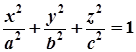. (3)

Площина перетинає цей еліпсоїд по еліпсу . Співставляючи останнє рівняння із (2), матимемо: . Тоді рівняння (3) набуде вигляду: .

За умовою точка 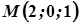лежить на цій поверхні, тому

,

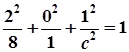звідки .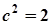

Тому рівняння даного еліпсоїда .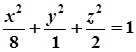

Відповідь: .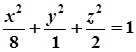

§7. Однопорожнинний гіперболоїд

Означення 7.1.

Однопорожнинним гіперболоїдом називається поверхня, яка в деякій прямокутній системі координат задається рівнянням

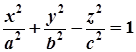. (1)

Це рівняння називається канонічним рівнянням однопорожнинного гіперболоїда, а система координат, в якій воно задане, – канонічною системою координат.

Дата добавления: 2015-03-31