
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Властивості гіперболічного параболоїда
|
|
|
|
Приклад
Знайти рівняння еліптичного параболоїда з вершиною в початку координат, вісь якого збігається з віссю 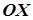 і якому належать точки
і якому належать точки 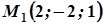 і
і 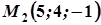 .
.
Розв’язання
Оскільки віссю еліптичного параболоїда є пряма 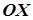 і абсциси точок на його поверхні додатні, то його канонічне рівняння має вигляд:
і абсциси точок на його поверхні додатні, то його канонічне рівняння має вигляд:
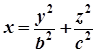 .
.
Підставимо координати даних точок у це рівняння і розв’яжемо систему:

Отже, шукане рівняння має вигляд
 .
.
Відповідь:  .
.
§ 10. Гіперболічний параболоїд
Означення 10.1. Гіперболічним параболоїдом називається поверхня, яка в деякій прямокутній системі координат задається рівнянням
 . (1)
. (1)
Це рівняння називається канонічним рівнянням гіперболічного параболоїда, а відповідна система координат – канонічною.
1. Гіперболічний параболоїд проходить через початок координат, і це єдина точка, в якій він перетинає координатні осі.
2. Гіперболічний параболоїд симетричний відносно координатних площин 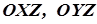 . Тому він симетричний і відносно осі
. Тому він симетричний і відносно осі 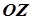 , яка називається його віссю. Точка, в якій ця вісь перетинає гіперболічний параболоїд, називається його вершиною.
, яка називається його віссю. Точка, в якій ця вісь перетинає гіперболічний параболоїд, називається його вершиною.
3. Якщо гіперболічний параболоїд перетнути площиною 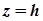 , паралельною до площини
, паралельною до площини  , то в перетині утвориться гіпербола
, то в перетині утвориться гіпербола
 ,
,
уявна вісь якої буде паралельною до осі 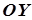 , якщо
, якщо  , і до осі
, і до осі 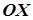 , якщо
, якщо 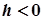 (рис. 7.29). Якщо ж
(рис. 7.29). Якщо ж 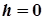 , то перетином буде пара прямих, що перетинаються:
, то перетином буде пара прямих, що перетинаються:
 ,
,
або

Якщо перетнути гіперболічний параболоїд площиною 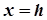 , паралельною до
, паралельною до 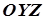 , то в перетині утвориться парабола
, то в перетині утвориться парабола
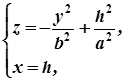 (2)
(2)
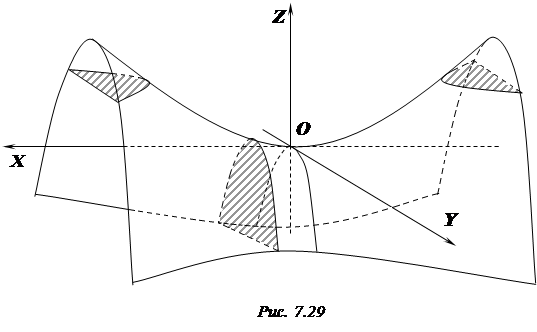 вітки якої напрямлені вниз (рис. 7.29).
вітки якої напрямлені вниз (рис. 7.29).
Якщо гіперболічний параболоїд перетнути площиною 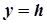 , паралельно до площини
, паралельно до площини 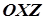 , то в перетині утвориться парабола
, то в перетині утвориться парабола
 (3)
(3)
вітки якої напрямлені вгору.
Зокрема, при перетині площиною 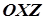 утвориться парабола
утвориться парабола
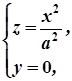 (4)
(4)
Координати вершини 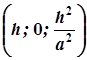 параболи (2) задовольняють рівняння (4). Отже, вершина параболи (2) лежить на параболі (4). Таким чином, гіперболічний параболоїд може бути утворений в результаті руху параболи (2), площина якої паралельна до площини
параболи (2) задовольняють рівняння (4). Отже, вершина параболи (2) лежить на параболі (4). Таким чином, гіперболічний параболоїд може бути утворений в результаті руху параболи (2), площина якої паралельна до площини 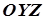 , так, щоб її вершина “ковзала” по параболі (3), яка лежить у перпендикулярній площині
, так, щоб її вершина “ковзала” по параболі (3), яка лежить у перпендикулярній площині 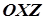 .
.
Поверхня, задана рівнянням  , також є гіперболічним параболоїдом, симетричним розглянутому відносно координатної площини
, також є гіперболічним параболоїдом, симетричним розглянутому відносно координатної площини  .
.
Якщо гіперболічний параболоїд задається рівнянням  або
або 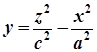 , то його віссю є пряма
, то його віссю є пряма 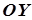 .
.
Якщо ж його рівняння  чи
чи  , то віссю є пряма
, то віссю є пряма 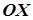 .
.
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 845; Нарушение авторских прав?; Мы поможем в написании вашей работы!