Приклад. Знайти рівняння площини, паралельної до однієї з координатних площин, яка перетинає двопорожнинний гіперболоїд по еліпсу з півосями і 2

Знайти рівняння площини, паралельної до однієї з координатних площин, яка перетинає двопорожнинний гіперболоїд 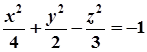по еліпсу з півосями 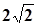і 2.

Розв’язання

Рівняння шуканої площини 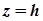, а рівняння її лінії перетину з двопорожнинним гіперболоїдом

,

або

.

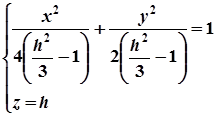За умовою задачі

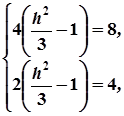
звідки .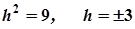

Отже, рівняння таких площин .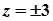

§ 9. Еліптичний параболоїд

Означення 9.1. Еліптичним параболоїдом називається поверхня, яка в деякій прямокутній системі координат задається рівнянням

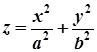. (1)

Це рівняння називають канонічним рівнянням еліптичного параболоїда.

З цього рівняння випливають такі властивості еліптичного параболоїда:

1. Еліптичний параболоїд проходить через початок координат, і це єдина точка, в якій він перетинає координатні осі.

2. Еліптичний параболоїд симетричний відносно координатних площин 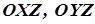, оскільки разом з точкою 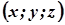його рівняння задовольняють точки 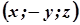, , 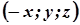симетричні відносно цих площин.

3. Еліптичний параболоїд симетричний відносно осі 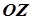, бо ця вісь є лінією перетину його площин симетрії. Вісь 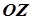називається віссю еліптичного параболоїда, а точка, в якій він перетинає цю вісь – вершиною.

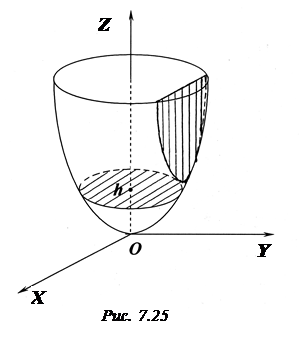
4. Якщо еліптичний параболоїд перетнути площинами 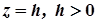, паралельними до площини , то в перетині утворяться еліпси 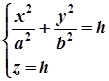, або 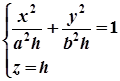. Розміри цих еліпсів збільшуються із збільшенням 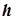(рис. 7.25).

Якщо еліптичний параболоїд перетнути площинами 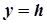, паралельними до площини 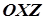, то в перетині утворяться параболи

, (2)

осі яких паралельні до осі .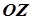

Якщо еліптичний парабалоїд перетнути площинами 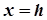, паралельними до 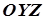, то в перетині утворяться параболи 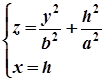, осі яких паралельні до осі .

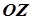Зокрема, в перерізі з площиною 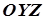утвориться парабола

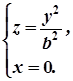(3)

Координати вершини параболи (2) задовольняють рівняння (3). Тому еліптичний параболоїд може бути утворений в результаті руху параболи (2), площина якої паралельна до площини 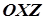, так, щоб її вершина рухалась по параболі (3), площина якої перпендикулярна до площин, в яких лежать перші параболи.

Зауваження. Якщо в рівнянні еліптичного параболоїда 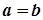, тобто 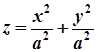, то одержимо параболоїд обертання, який утворюється з параболи

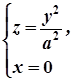
обертанням її навколо осі .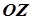

Якщо рівняння еліптичного параболоїда 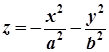, то він розташований в іншому півпросторі відносно площини , ніж еліптичний параболоїд (1) (рис. 7.26).

Еліптичний параболоїд, заданий рівнянням 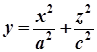, матиме своєю віссю вісь 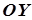(рис. 7.27).

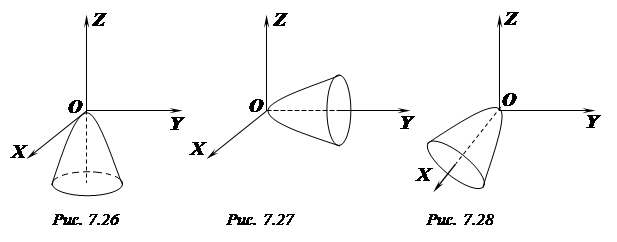
Якщо еліптичний параболоїд має рівняння 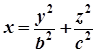, то його віссю буде вісь 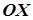(рис. 7.28).

Дата добавления: 2015-03-31