Прямолінійні твірні гіперболічного параболоїда

Розглянемо гіперболічний параболоїд, заданий канонічним рівнянням

. (7)

Перетворимо це рівняння так:

.

Розглянемо дві системи рівнянь:

і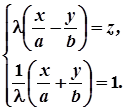

Ці системи визначають рівняння прямих, які повністю лежать на гіперболічному параболоїді, бо якщо перемножити відповідні частини рівнянь однієї системи, то одержимо рівняння (7) при довільному 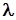, відмінному від нуля.

Ці прямі називаються прямолінійними твірними гіперболічного параболоїда. Вони мають такі ж властивості, як і прямолінійні твірні однопорожнинного гіперболоїда:

1. Через довільну точку гіперболічного параболоїда проходить одна і тільки одна твірна з кожної сім’ї.

2. Будь-які дві твірні однієї сім’ї є мимобіжними.

3. Будь-які дві твірні різних сімей перетинаються або паралельні.

Пропонуємо довести ці властивості самостійно.

Таким чином, гіперболічний параболоїд також є лінійчатою поверхнею (рис. 7.31).

Можна показати, що однопорож­нин­ний гіперболоїд утворюється ру­хом прямої, яка ковзає по трьох мимобіжних прямих. Аналогічно гіперболічний параболоїд можна утворити рухом прямої, яка ковзає по двох мимобіжних прямих і залишається при цьому весь час паралельною заданій площині.

Природно виникає запитання: чи мають прямолінійні твірні такі поверхні другого порядку як еліпсоїд, двопорожнинний гіперболоїд і еліптичний параболоїд?

Відповідь проста: ні. Покажемо це на прикладі еліпсоїда. Як було встановлено в §6, еліпсоїд лежить всередині деякого прямокутного паралелепіпеда, тобто є обмеженою поверхнею. Але кожна пряма є необмеженою лінією, а тому не може повністю лежати на еліпсоїді.

Дата добавления: 2015-03-31