Приклад 2

Приклад 1.

Записати рівняння дотичної площини до еліпсоїда 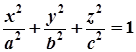у його точці .

Розв’язання

Для еліпсоїда . За формулою (7)

,

або

.

Записати рівняння дотичної площини до еліптичного параболоїда .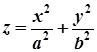

Розв’язання

Для цієї поверхні

,

За формулою (7):

,

або

.

Пропонуємо самостійно переконатися, що дотичною площиною

– до однопорожнинного гіперболоїда 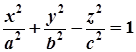є площина ;

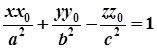– до двопорожнинного гіперболоїда –площина ;

– до гіперболічного параболоїда – площина ;

– до конічної поверхні 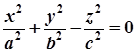– площина .

§ 15. Площини симетрії поверхні другого порядку

Означення 15.1. Площина називається площиною симетрії поверхні, якщо разом з довільною точкою М цій поверхні належить і точка 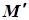, симетрична точці М відносно площини .

Нехай у деякій прямокутній системі координат поверхня другого порядку задана загальним рівнянням

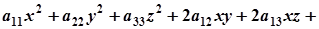
. (1)

Нехай ця поверхня має площину симетрії, нормальний вектор якої (рис. 7.34). Тоді ця площина симетрії буде діаметральною площиною, спряженою з напрямком, який задається вектором . Тому її рівняння запишеться так:

,

або

;

.

Коефіцієнти при змінних у цьому рівнянні є координатами нормального вектора до даної площини, який буде колінеарним до вектора , тому координати цих векторів пропорційні. Отже, справджується така рівність:

.

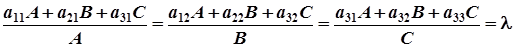Звідси, беручи до уваги, що 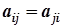, дістанемо:

(2)

Ця система матиме ненульовий розв’язок відносно (А, В, С) тоді і тільки тоді, коли її визначник дорівнює нулю:

. (3)

Рівняння (3) називається характеристичним рівнянням даної поверхні.

Оскільки матриця , є симетричною, то, як відомо з алгебри, її власні числа (корені рівняння (3)) будуть дійсними. Розв’язавши рівняння (3) і знайшовши його корені , необхідно підставити їх по черзі в систему (2). Розв’язуючи систему (2) для кожного , знайдемо координати 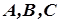відповідних нормальних векторів площин симетрії. Залежно від того, скільки розв’язків має система (2), поверхня може мати різну кількість площин симетрії або не мати жодної.

Знайшовши координати вектора 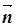, одразу можна записати рівняння площини симетрії як відповідної діаметральної площини.

Приклад

Знайти площини симетрії поверхні

.

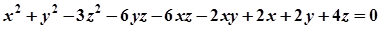Розв’язання

1. Складемо і розв’яжемо характеристичне рівняння

;

;

;

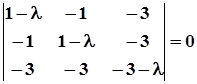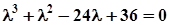Отже, .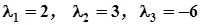

2. Для кожного з коренів характеристичного рівняння знаходимо із системи (3) відповідний нормальний вектор шуканої площини симетрії

Нехай . Тоді . Отже, .

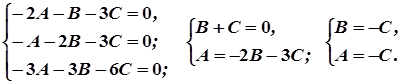
Нехай 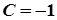, тоді , .

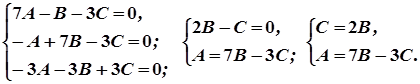
Нехай , тоді .

3. Записуємо рівняння площин симетрії як рівняння діаметральних площин, спряжених до знайдених напрямків (формула (8) § 12). Для цієї поверхні

Тому рівняння площин симетрії такі:

1) ;

;

.

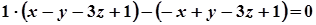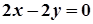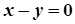2) .

;

.

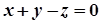3) .

;

.

Відповідь: .

§ 16. Зведення загального рівняння поверхні

другого порядку до канонічного вигляду

Нехай у деякій прямокутній системі координат поверхня другого порядку задана загальним рівнянням

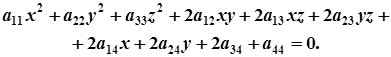(1)

Розглянемо вираз

, (2)

який називається квадратичною формою даної поверхні.

Дата добавления: 2015-03-31