
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Введемо позначення
|
|
|
|
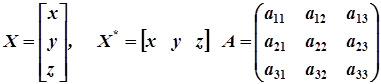 .
.
Тоді вираз (2) можна записати у вигляді  . Дійсно
. Дійсно
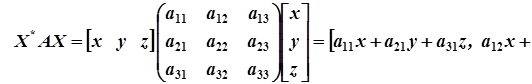
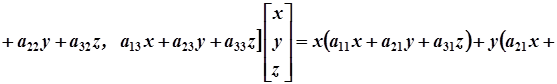

 .
.
Таким чином,
 . (3)
. (3)
Поставимо тепер завдання знайти таку нову систему координат 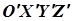 , у якій рівняння даної поверхні матиме найпростіший вигляд. Припустимо спочатку, що початки нової і старої систем координат збігаються. Тоді формули перетворення мають вигляд:
, у якій рівняння даної поверхні матиме найпростіший вигляд. Припустимо спочатку, що початки нової і старої систем координат збігаються. Тоді формули перетворення мають вигляд:
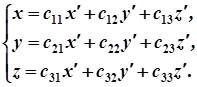 (4)
(4)
Наша задача полягає в тому, щоб за допомогою перетворення (4) звести квадратичну форму (3) до якомога простішого вигляду. Введемо позначення:
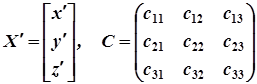 .
.
Тоді формули (4) запишуться у вигляді
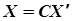 . (5)
. (5)
Якщо формулу (5) підставити у (3), то квадратична форма  зводиться до такого вигляду:
зводиться до такого вигляду:
 .
.
Таким чином, в результаті даного перетворення квадратична форма  зводиться до іншого квадратичної форми
зводиться до іншого квадратичної форми  із змінними
із змінними 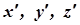 і новою матрицею
і новою матрицею  , де С* - матриця, транспонована з матрицею С.
, де С* - матриця, транспонована з матрицею С.
Тому, щоб звести квадратичну форму (3) до найпростішого вигляду, треба підібрати перетворюючу матрицю С таким чином, щоб матриця  мала найпростіший вигляд.
мала найпростіший вигляд.
Виявляється, що матриця  матиме найпростіший вигляд, якщо її стовпцями будуть власні вектори матриці А, які відповідають власним значенням
матиме найпростіший вигляд, якщо її стовпцями будуть власні вектори матриці А, які відповідають власним значенням  . При цьому необхідно, щоб ці власні вектори утворювали ортонормований базис.
. При цьому необхідно, щоб ці власні вектори утворювали ортонормований базис.
Дійсно, нехай

є власними векторами матриці А, які відповідають її власним значенням  . Це означає, що виконуються рівності
. Це означає, що виконуються рівності 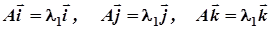 . Будемо вважати, що вектори
. Будемо вважати, що вектори  одиничні й ортогональні. Складемо матрицю С з координат цих векторів
одиничні й ортогональні. Складемо матрицю С з координат цих векторів
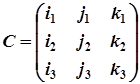 .
.
Тоді
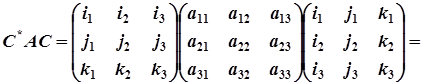
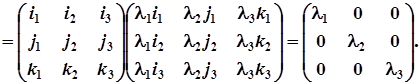
Таким чином, у новій системі координат координатними векторами якої є ортонормовані власні вектори 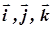 матриці А, квадратична форма набуває вигляду
матриці А, квадратична форма набуває вигляду


Тому якщо від системи координат  перейти до нової системи координат
перейти до нової системи координат 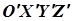 , координатними векторами якої є ортонормована система власних векторів матриці А, то в цій системі рівняння поверхні зведеться до вигляду
, координатними векторами якої є ортонормована система власних векторів матриці А, то в цій системі рівняння поверхні зведеться до вигляду
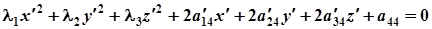 .
.
За допомогою паралельного перенесення системи координат це рівняння можна спростити ще більше. В результаті цього неважко переконатися, що довільна поверхня другого порядку є або еліпсоїдом, або однопорожнинним чи двопорожнинним гіперболоїдом, або еліптичним чи гіперболічним параболоїдом, або конусом, або еліптичним, гіперболічним чи параболічним циліндром, або ж парою площин, які можуть перетинатися, бути паралельними чи збігатися. Причому поверхня може бути і уявною, наприклад,  – уявний еліпс,
– уявний еліпс, 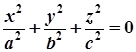 – уявний конус.
– уявний конус.
З цих міркувань випливає такий алгоритм зведення загального рівняння поверхні другого порядку до канонічного виду:
1. Складаємо характеристичне рівняння поверхні другого порядку
 (6)
(6)
і знаходимо його корені 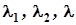 .
.
2. Знаходимо власні вектори матриці А, які відповідають знайденим власним значенням, розв’язуючи рівняння:
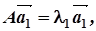
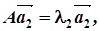

Оскільки матриця А симетрична, то при різних значеннях коренів рівняння (6) власні вектори будуть попарно ортогональними. Якщо ж система (6) має кратні корені, то для кратного кореня потрібно підібрати відповідні ортогональні власні вектори. У кожному випадку ці вектори потрібно пронормувати, взявши замість них одиничні вектори

3. Складаємо формули переходу від системи координат  до нової системи
до нової системи  :
:
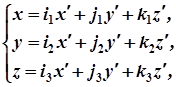
в яких коефіцієнти при змінних  є координатами знайдених базисних векторів.
є координатами знайдених базисних векторів.
4. Підставляємо ці формули у початкове рівняння (1), в результаті чого воно зведеться до вигляду
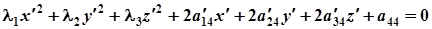 .
.
5. Виділяючи в одержаному рівнянні повні квадрати і застосовуючи паралельне перенесення системи координат, зводимо рівняння даної поверхні до канонічного вигляду.
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 615; Нарушение авторских прав?; Мы поможем в написании вашей работы!