
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема 12.1
|
|
|
|
Середини паралельних хорд поверхні другого порядку лежать на площині.
Доведення
Нехай поверхня другого порядку задана загальним рівнянням у деякій системі координат  :
:
 (1)
(1)
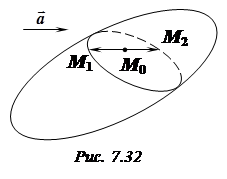 Розглянемо хорди цієї поверхні, паралельні до заданого вектора
Розглянемо хорди цієї поверхні, паралельні до заданого вектора  (рис. 7.32). Нехай
(рис. 7.32). Нехай 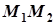 – одна з таких хорд, точка
– одна з таких хорд, точка  – її середина, координати кінців хорди:
– її середина, координати кінців хорди:  і
і 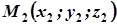 . Розглянемо вектори
. Розглянемо вектори 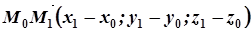 і
і 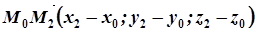 . Ці вектори колінеарні з вектором
. Ці вектори колінеарні з вектором  , причому один з них співнапрямлений з вектором
, причому один з них співнапрямлений з вектором  , а другий – протилежно напрямлений з
, а другий – протилежно напрямлений з  . Довжини цих векторів рівні. Тому
. Довжини цих векторів рівні. Тому  ,
, 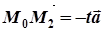 , де t – деяке число, відмінне від нуля. Тоді
, де t – деяке число, відмінне від нуля. Тоді
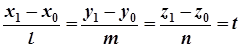 ,
,
 ,
,
звідки
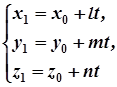 (2)
(2)
і
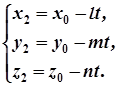 (3)
(3)
Точки  і
і 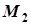 лежать на даній поверхні, тому їх координати задовольняють рівняння (1). Підставивши (2) в (1), матимемо:
лежать на даній поверхні, тому їх координати задовольняють рівняння (1). Підставивши (2) в (1), матимемо:



Беручи до уваги, що 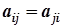 , дістанемо
, дістанемо
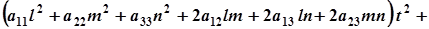
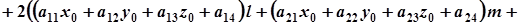

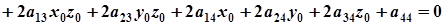 (4)
(4)
Введемо позначення:

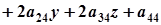 ;
;
 ;
;
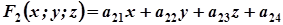 ;
;
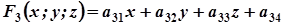 ;
;
Тоді рівність (4) запишеться так:
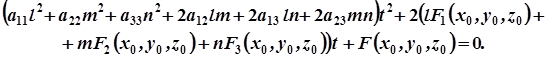 (5)
(5)
Аналогічно, підставивши (3) в (1), матимемо:
 (6)
(6)
Віднявши відповідні частини (5) і (6), дістанемо:
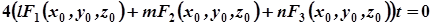 ,
,
звідки випливає, що координати точки  задовольняють рівняння
задовольняють рівняння
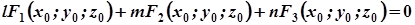 . (7)
. (7)
А це є рівняння першого порядку відносно 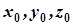 .
.
Цим самим ми встановили, що для того, щоб точка  хорди, паралельної до вектора
хорди, паралельної до вектора 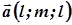 , була її серединою, необхідно і достатньо, щоб її координати задовольняли рівняння (7), яке є рівнянням площини. Теорему доведено.
, була її серединою, необхідно і достатньо, щоб її координати задовольняли рівняння (7), яке є рівнянням площини. Теорему доведено.
Означення 12.2. Площина, яка проходить через середини хорд поверхні другого порядку, паралельних до деякого вектора  , називається діаметральною площиною цієї поверхні, спряженою з вектором
, називається діаметральною площиною цієї поверхні, спряженою з вектором  .
.
Як випливає з наведених вище міркувань, рівняння діаметральної площини, спряженої з вектором  , має вигляд:
, має вигляд:
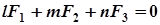 (8)
(8)
Приклад. Скласти рівняння діаметральної площини поверхні 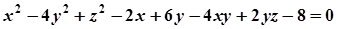 , спряженої з вектором
, спряженої з вектором  .
.
Розв’язання
Для даної поверхні
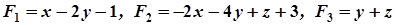 .
.
Із рівняння (8) маємо:
 ;
;
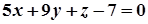 .
.
Відповідь. 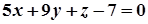 .
.
§13. Центр поверхні другого порядку
Означення 13.1. Точка О називається центром поверхні другого порядку, якщо разом з довільною точкою М цієї поверхні їй належить і точка 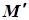 , симетрична відносно точки О.
, симетрична відносно точки О.
Нехай у деякій системі координат поверхня другого порядку задана загальним рівнянням
 (1)
(1)
 Точка
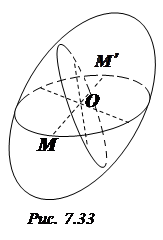
Точка  буде центром даної поверхні тоді і тільки тоді, коли вона буде серединою будь-якої хорди, яка проходить через неї. Це означає, що всі діаметральні площини поверхні проходять через точку О, тому координати точки О задовольняють рівняння довільної діаметральної площини (рис. 7.33):
буде центром даної поверхні тоді і тільки тоді, коли вона буде серединою будь-якої хорди, яка проходить через неї. Це означає, що всі діаметральні площини поверхні проходять через точку О, тому координати точки О задовольняють рівняння довільної діаметральної площини (рис. 7.33):
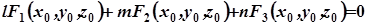 . (2)
. (2)
Отже, точка  буде центром даної поверхні тоді і тільки тоді, коли при довільних
буде центром даної поверхні тоді і тільки тоді, коли при довільних  виконується рівність (2).
виконується рівність (2).
А це можливо тоді і тільки тоді, коли виконуються рівності

Отже, щоб знайти центр поверхні (1), необхідно розв’язати систему рівнянь:
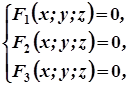
або
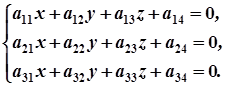 (3)
(3)
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 652; Нарушение авторских прав?; Мы поможем в написании вашей работы!