Приклад

Записати канонічне рівняння гіперболічного параболоїда, який перетинає площину 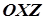по параболі 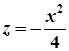, а площину 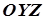– по параболі .

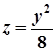Розв’язання

Шуканий гіперболічний параболоїд перетинає по параболах координатні площини 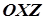і 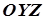, тому його віссю є пряма 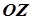, а рівняння має вигляд

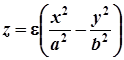, де .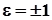

Перетин такої поверхні з площиною 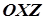в системі координат 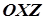задається рівнянням

.

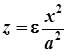Співставляючи з умовою задачі, доходимо висновку, що 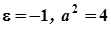. Аналогічно перетином з площиною 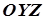є лінія, що у відповідній системі координат задається рівнянням

,

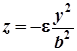звідки .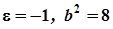

Отже, рівняння шуканої поверхні

,

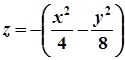або

.

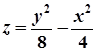Відповідь: .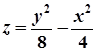

§ 11. Прямолінійні твірні на поверхні другого порядку

Виявляється, що не тільки циліндричні і конічні поверхні можуть утворитися з прямих ліній. Такими властивостями володіють також однопорожнинний гіперболоїд і гіперболічний параболоїд.

11.1. Прямолінійні твірні на поверхні однопорожнинного гіперболоїда

Розглянемо однопорожнинний гіперболоїд, заданий канонічним рівнянням

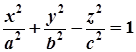. (1)

Перетворимо це рівняння таким чином:

;

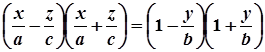. (2)

Розглянемо тепер дві сім’ї прямих, заданих системами рівнянь

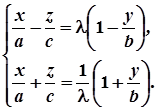(3)

і

(4)

де 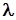– довільне дійсне число, відмінне від нуля.

Кожна з цих прямих повністю лежить на поверхні (1). Дійсно, якщо координати деякої точки задовольняють систему (3), то, перемноживши рівності цієї системи, одержимо рівняння (2), а, отже, і рівняння (1). Таким чином, довільна точка прямої (3) лежить на поверхні (1).

Аналогічно і будь-яка точка прямої (4) лежить на поверхні (1).

Таким чином, сім’ї прямих (3), (4) повністю лежать на однопорожнинному гіперболоїді. Вони називаються прямолінійними твірними цього гіперболоїда.

Ці твірні мають такі властивості:

1. Через кожну точку однопорожнинного гіперболоїда проходить одна і тільки одна твірна з кожної сім’ї.

Доведення

Нехай 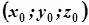– координати деякої точки однопорожнинного гіперболоїда, тоді

,

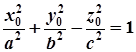звідки

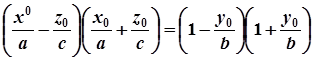. (5)

Виберемо тепер параметр 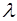так, щоб ця точка належала першій з площин системи (3). Для цього розв’яжемо рівняння

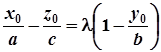. (6)

Поділивши почленно (5) на (6), дістанемо

.

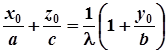Отже, дана точка належить і другій площині системи (3). Таким чином, яка б не була точка 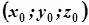, що лежить на однопорожнинному гіперболоїді, параметр 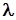завжди можна вибрати так, щоб координати точки задовольняли систему (3). Причому цей параметр визначається із рівняння (6) однозначно.

Отже, через кожну точку однопорожнинного гіперболоїда проходить єдина пряма із першої сім’ї.

Аналогічно доводиться це твердження і для другої сім’ї твірних.

2. Будь-які дві твірні однієї сім’ї не перетинаються і не паралельні, тобто є мимобіжними.

Доведення

Дійсно, ці прямі не можуть перетинатися, бо інакше через точку їх перетину проходило б дві твірні однієї сім’ї, що суперечить властивості 1.

Ці прямі не можуть бути і паралельними. Щоб переконатися в цьому, покажемо, що напрямні вектори прямих (3) при різних значеннях параметра 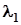і 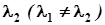неколінеарні.

Знайдемо координати напрямного вектора прямої (3). Перепишемо систему (3) у вигляді:

Напрямним вектором даної прямої є

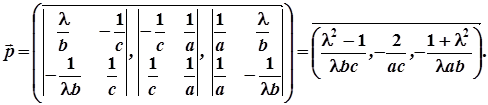
Напрямні вектори двох прямих із цієї сім’ї, що відповідають параметрам 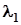і , такі:

,

.

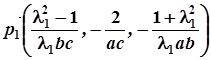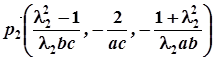Перевіримо, чи можуть бути вони колінеарними. Прирівнявши відношення відповідних координат, матимемо:

,

звідки

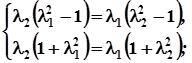
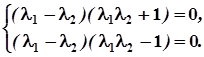
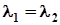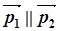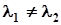Ця система сумісна, якщо . Отже, тоді і тільки тоді, коли . Якщо ж то 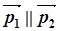. Це і доводить, що прямі не паралельні. Отже, вони мимобіжні.

3. Довільні дві твірні різних сімей перетинаються або паралельні.

Доведення

Розглянемо дві довільні твірні з різних сімей, при цьому нехай твірній із першої сім’ї відповідає параметр 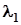, а з другої – . Щоб з’ясувати питання про перетин цих прямих, необхідно дослідити систему рівнянь

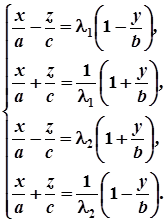
Оскільки одне з рівнянь системи є наслідком трьох інших (наприклад, 4-е рівняння утворюється внаслідок почленного множення перших двох і ділення на відповідні частини третього рівняння), то дослідимо систему з трьох перших рівнянь

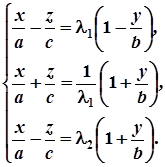або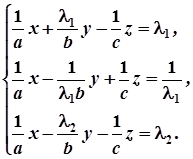

Визначник цієї системи

.

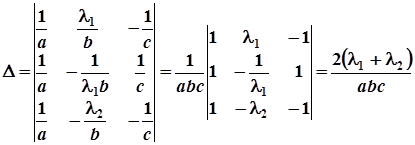Якщ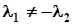о , то 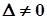. Отже, система має єдиний розв’язок, а значить, прямі перетинаються.

Якщ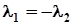о , то 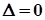, а самі прямі паралельні.

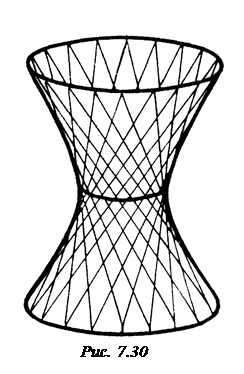Таким чином, однопорожнинний гіперболоїд є лінійчатою поверхнею (рис. 7.30). Ця властивість широко використо­вується в будівельній техніці. Відомий російський інженер Володимир Григорович Шухов запропонував конструкцію з металевих балок, розміщених так, як прямолінійні твірні однопорожнинного гіперболоїда обертання. Ці конструкції виявилися дуже міцними і легкими. Вони часто використовуються при будівництві водонапірних башт, високих радіо і телещогл.

Дата добавления: 2015-03-31