
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Властивості еліпсоїда
|
|
|
|
1. Еліпсоїд не проходить через початок координат, бо координати точки 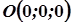 не задовольняють рівняння (1).
не задовольняють рівняння (1).
2. Еліпсоїд перетинає кожну із координатних осей у двох точках, симетричних відносно початку координат, а саме:
вісь 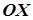 у точках
у точках 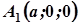 і
і 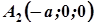 ,
,
вісь 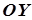 у точках
у точках 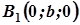 і
і 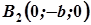 ,
,
вісь 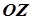 у точках
у точках 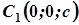 і
і 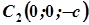 .
.
Ці точки називаються вершинами еліпсоїда, відрізки 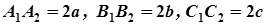 – осями еліпсоїда, числа
– осями еліпсоїда, числа 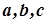 – півосями еліпсоїда.
– півосями еліпсоїда.
3. Еліпсоїд симетричний відносно всіх координатних площин, координатних осей і початку координат, бо всі змінні входять у його рівняння в парних степенях.
4. Із рівняння (1) випливає, що 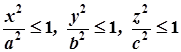 , тобто
, тобто 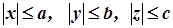 , або
, або 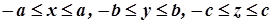 .
.
Це означає, що еліпсоїд є обмеженою поверхнею, яка міститься всередині прямокутного паралелепіпеда, обмеженого площинами: 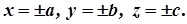
5. Якщо еліпсоїд перетнути площиною 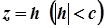 , паралельною площині
, паралельною площині  , то в перетині утвориться еліпс, рівняння проекції якого на площину
, то в перетині утвориться еліпс, рівняння проекції якого на площину  у системі координат цієї площини має вигляд:
у системі координат цієї площини має вигляд:
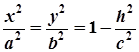 або
або 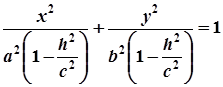 .
.
Розміри цього еліпса збільшуються із зменшенням 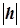 і зменшуються із збільшенням
і зменшуються із збільшенням 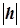 .
.
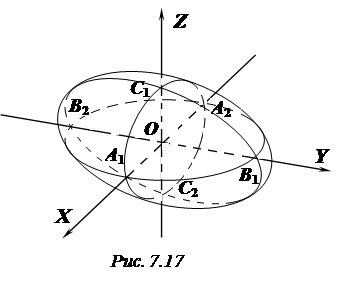 Аналогічна ситуація матиме місце і при перетині еліпсоїда площинами, паралельними до інших координатних площин.
Аналогічна ситуація матиме місце і при перетині еліпсоїда площинами, паралельними до інших координатних площин.
Виходячи із цих влас-тивостей, можна побуду-вати зображення еліпсоїда (рис. 7.17).
Якщо у рівнянні (1) два параметри рівні між собою, наприклад, а=b, то отримаємо поверхню обер-тання – еліпсоїд обертання:
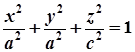 , або
, або 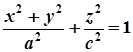 .
.
Ця поверхня утворена внаслідок обертання еліпса з півосями а, с навколо осі OZ.
Якщо ж a=b=c, то із (1) матимемо: 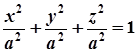 , або
, або 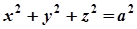 .
.
Це рівняння сфери з центром у початку координат. Отже, сфера є частинним випадком еліпсоїда.
Справедлива й така теорема:
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 1284; Нарушение авторских прав?; Мы поможем в написании вашей работы!