Применение формулы Полной вероятности

Закон распределения случайных величин (СВ) для дискретных и непрерывных СВ. (Показать на примерах)

Приведите примеры непрерывных случайных величин (СВ) в экономике.

Приведите примеры дискретных случайных величин (СВ) в экономике.

Дискретные Число институциональных инвесторов вложивших ср-ва в облигацию

Непрерывные YTM облигации

21.22 Перечислите основные числовые характеристики СВ. Как они вычисляются для дискретных СВ? Как они вычисляются для непрерывных СВ?

Числовые характеристики (ЧХ) СВ выражают наиболее существенные черты ее распределения. Наиб.важные из них: матожидание, дисперсия, ср.квадр.откл-е и др.

ДСВ

Матожидание= сумма произведений всех ее значений на соответств-е им вероятности

Дисперсия =матожидание квадрата отклонения СВ от матожидания =М(Х-а)²

НСВ

23. Что называют законом распределения случайной величины (СВ) и что он показывает?

Наиболее полным описанием СВ является закон ее распределения (ЗР)- всякое соотношение, устанавливающее связь между возможными значениями СВ и соответствующими им вероятностями.

Для ДСВ ЗР мб представлен:

- в виде таблицы (ряда распределения ДСВ)

- в виде формулы (аналитически)

- графически (полигон распределения вероятности)

Если известны вероятности гипотезы Р(О1), Р(О2),......., Р(Оn) и условные вероятности

Р (А/О1), Р (А/О2),......, Р (А/Оn), то применяется формула Полной вероятности.

Р(A)= Р(О1)* Р (А/О1) + Р(О2)* Р (А/О2)+ ……+ Р(Оn) * Р (А/Оn)

Пример: в первой урне содержится 20 шаров, из которых 16 –черные. Во втророй урне находится 10 шаров, из которых 6- черные. Из второй урны случайным образом извлекается шар и перекладывается в первую. Найти вероятность того, что шар случайным образом взятый из первой урны, будет черным.

Решение: О- событие, состоящее в извлечении из первой урны черного шара.

Из второй урны мог быть извлечен либо черный шар (событие О1), либо шар другого цвета (событие О2). Вероятность того что из второй урны извлечен черный шар:

Р(О1)=6/10, Р(О2)=4/10

Р (А/О1)= 17/21 Р(A)= 0,08

Р (А/О2)= 16/21

26. В каких случаях применяют формулу Байеса? (Показать на примерах)

Теорема. Вероятность произведения двух независимых событий, равна произведению вероятностей этих событий, т.е.

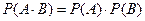
Дата добавления: 2015-04-23