Прямая на плоскости. Различные формы уравнения прямой

Параметрические уравнения линий и поверхностей.

№38. Построить линию, определяемую уравнениями: 1). x = sin t, y = cosec t; 2). x = t², y = 3t.

№39. Какая линия определяется параметрическими уравнениями x = cos t, y = cos² t?

Ответ: Парабола.

№40. Кривая задана параметрическими уравнениями n=1+n ∙ cos t, у =2n · sin t. Найти каноническое уравнение этой линии в декартовых прямоугольных координатах. Построить кривую.

Ответ: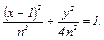

№41. Составить уравнение сферы в каждом из следующих случаев:

а). сфера проходит через точку М(3; -1; 4) и имеет центр С(1; -3; 5).

б). точки М(4; -3; 7) и N(2; 1; 3) являются концами одного из ее диаметров;

в). сфера проходит через четыре точки: А(1; 1; 0), В(7;-11; 0), С(10; 1; 9), D(-2;-11; 9).

Ответ: а)

б)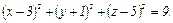

в)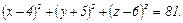

№42. Найти центр и радиус сферы 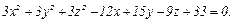Лежат ли на этой сфере точки А(3; -2; 1), В(1; 0; 0) и С(2; 1;3)?

Ответ: (2; -2,5; 1,5); . На сфере лежит точка А.

Тема 2. Уравнения прямых и плоскостей. Приложение векторной алгебры к задачам аналитической геометрии.

№43. Написать уравнение прямой, проходящей через точки А(0; -2) и В(-5;3). Проходит ли прямая АВ через точку пересечения прямых х -3у -2 = 0 и 2х +5у + 7 = 0?

Ответ: x + y + 2 = 0. Проходит.

№44. Даны уравнения двух сторон 2х -3у +5 = 0 и 3х + 2у -7 = 0 прямоугольника и одна из его вершин О(0; 0). Составить уравнения двух других сторон.

Ответ: 2x – 3y = 0; 3x + 2y = 0.

№45. Прямая проходит через точку А(2; -3) и отсекает на оси ординат отрезок длиной 3. Найти уравнение прямой.

Ответ: y = -3 или 3x + y – 3 = 0.

№46. Дан треугольник с вершинами А(-2; 0), В(2; 4) и С(4; 0).

Найти уравнения стороны ВС и медианы АЕ. Вычислить длину медианы.

Ответ: BС: 2x + y - 8 = 0; AE: 2x – 5y + 4; .

№47. Определить все значения а, при которых точка М(1; 5)принадлежит внутренней области треугольника с вершинами А(2; -1), В(0; а) и С(4; 0).

Ответ:

№48. Даны точки L(-6; 0) и N(0; 8). Через середину отрезка LN провести прямую, отсекающую на оси х отрезок втрое больший, чем на оси у.

Ответ: x + 3y – 9 = 0.

№49. Вычислить площадь треугольника, стороны которого лежат на прямых 8х – nу + 5n =0,
х + 2у – 10 = 0 и 3х – (n+10) у – 30 = 0.

Ответ: S = 2,5n + 40.

№50. Найти уравнение высоты треугольника с основанием на прямую х – у + 2 = 0 и боковыми сторонами на прямых 5х + 2у + 2n – 5 =0 и 3х + 10у + 10 n – 3 = 0.

Ответ: x + y + n - 1 = 0

№51. Найти точку, симметричную точке М(5; 5) относительно прямой х + у – 3 = 0.

Ответ: (-2; -2).

№52. Найти проекцию точки М(-5; 4) на прямую х – у – 5 =0.

Ответ: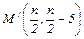

№53. Даны две стороны х – у + 1 = 0 и 3х + 2у – 12 = 0 параллелограмма и точка Е(6; 4) пересечения его диагоналей. Найти уравнения двух других сторон.

Ответ: x – y – 5 = 0; 3x + 2y – 40 = 0.

№54. Найти уравнение общей хорды окружносте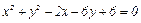й и .

Ответ: x + y – 6 = 0.

Дата добавления: 2015-04-24