
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кратчайшим расстоянием от точки А до прямой р является перпендикуляр АС, опущенный из точки А на прямую р
|
|
|
|
Определение 4. Расстоянием от точки до прямой называется перпендикуляр, опущенный из точки на данную прямую.
| В1 |
| С1 |
| B |
| А1 |
| C |
| A |
Теорема 1 (первый признак равенства треугольников – СУС). Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Дано: ∆АВС; ∆А1В1С1; АВ = А1В1; ÐA = ÐA1; АС = А1С1.
Доказать: ∆АВС = ∆А1В1С1.
Доказательство:
1. Наложим ∆АВС на ∆А1В1С1 так, чтобы точка А совместилась с точкой А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и А1С1.
2. Поскольку АВ = А1В1, точки В и В1 совпадут, а сторона АВ совместится со стороной А1В1.
3. Поскольку АС = А1С1, точки С и С1 совпадут, а сторона АС совместится со стороной А1С1.
4. Согласно аксиоме существования прямых стороны ВС и В1С1 также совпадут. ∆АВС = ∆А1В1С1.
Теорема 2 (второй признак равенства треугольников – УСУ). Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Дано: ∆АВС; ∆А1В1С1; ÐA = ÐA1; АС = А1С1; ÐС = ÐС1.
Доказать: ∆АВС = ∆А1В1С1.
Доказательство:
1. Наложим ∆АВС на ∆А1В1С1 так, чтобы точка А совместилась с точкой А1, сторона АС – с равной ей стороной А1С1, а вершины В и В1 оказались по одну сторону от прямой А1С1.
2. Поскольку ÐA = ÐA1 и ÐС = ÐС1, то сторона АВ наложится на луч А1В1, а сторона СВ наложится на луч С1В1. Вершина В – общая точка сторон АВ и СВ – окажется лежащей на лучах А1В1 и С1В1, а следовательно, совместится с общей точкой лучей А1В1 и С1В1, т. е. с точкой В1. Значит, совместятся стороны АВ и А1В1, а также СВ и С1В1. Значит, ∆АВС = ∆А1В1С1.
| A1 |
| В1 |
| B |
| С (С1) |
| В1 |
| С1 |
| A (A1) |
| C |
| B |
| A |
Дано: ∆АВС; ∆А1В1С1; АВ = А1В1; ВС = В1С1; АС = А1С1. Доказать: ∆АВС = ∆А1В1С1.
Доказательство:
1. Дополнительное построение. Приложим ∆АВС к ∆А1В1С1 так, чтобы вершина А совместилась с вершиной А1 и вершина С совместилась с вершиной С1, а вершина В и вершина В1 оказались по разные стороны от отрезка АС.
2. Возможны три случая: 1) луч ВВ1 проходит внутри угла АВС; 2) луч ВВ1 совпадает с одной из сторон угла АВС; 3) луч ВВ1 проходит вне угла АВС.
3. Рассмотрим первый случай. Так как АВ = А1В1, то ∆АВВ1 – равнобедренный Þ
Ð АВВ1 = ÐАВ1В (углы при основании). Так как СВ = СВ1, то ∆СВВ1 – равнобедренный Þ ÐСВВ1 = ÐСВ1В (углы при основании).
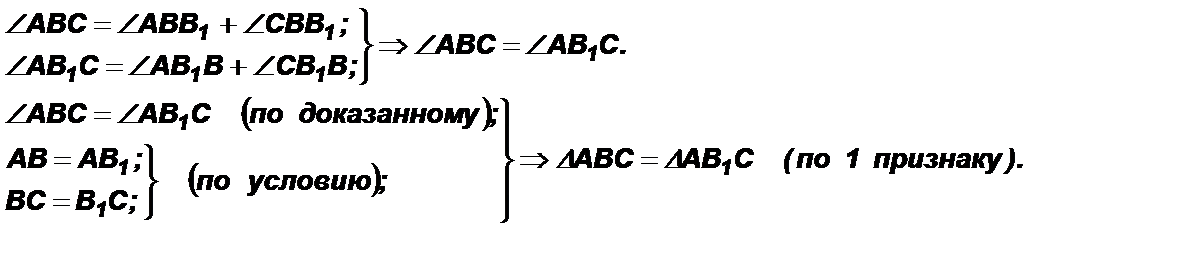
4. Рассмотрим второй случай. Пусть точка СÌВВ1. Так как АВ = А1В1, то ∆АВВ1 – равнобедренный Þ
Ð АВВ1 = ÐАВ1В (углы при основании). Так как СВ = СВ1, то в ∆АВВ1 АС – медиана.
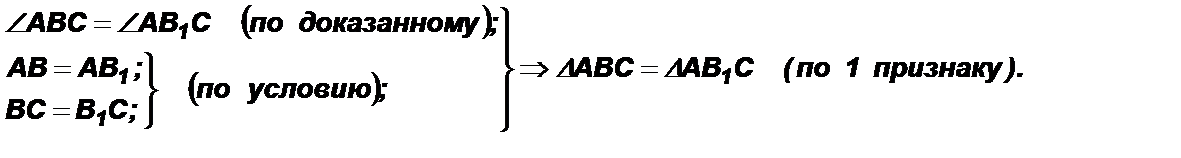
3. Рассмотрим третий случай. Так как АВ = А1В1, то ∆АВВ1 – равнобедренный Þ
Ð АВВ1 = ÐАВ1В (углы при основании). Так как СВ = СВ1, то ∆СВВ1 – равнобедренный Þ ÐСВВ1 = ÐСВ1В (углы при основании).

Определение 1. Равнобедренным называется треугольник, у которого две стороны равны.
Равные стороны равнобедренного треугольника называются боковыми, а третья сторона – основанием. Общая вершина двух равных (боковых) сторон называется вершиной равнобедренного треугольника.
| P |
| М |
| К |
| С |
| В |
| А |
Определение 3. Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны. CM – медиана, проведенная к стороне АВ, при этом АМ = МВ.
Определение 4. Высотой треугольника называется отрезок перпендикуляра, опущенный из вершины треугольника на противоположную сторону. ВР – высота, опущенная на сторону АС.
Свойства равнобедренного треугольника.
| D |
| C |
| B |
| A |
Дано: ∆АВС; АВ = ВС. Доказать: ÐА = ÐС.
Доказательство:
1. Дополнительное построение. Проведем отрезок BD – биссектрису ÐАВС.
2. ÐABD = ÐDBC =  (по свойству биссектрисы).
(по свойству биссектрисы).

4. Из ∆ABD = ∆DBC Þ ÐA = ÐC.
Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является его медианой и высотой.
Дано: ∆АВС; АВ = ВС. Доказать: BD – медиана, BD – высота.
Доказательство:

2. Из ∆ABD = ∆DBC Þ AD = DC Þ ВD – медиана по определению.
3. Из ∆ABD = ∆DBC Þ ÐADВ = ÐВDC.
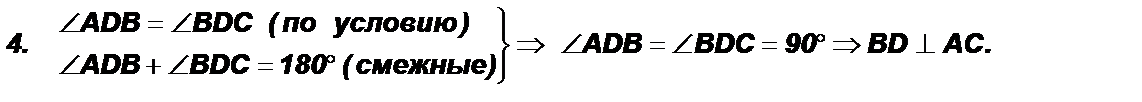
3. Признаки параллельности прямых. Следствия. Теорема о углах соответственно параллельными сторонами.
Теорема 1. Две прямые, перпендикулярные к третьей прямой, не пересекаются (параллельны).
Дано: а – прямая; 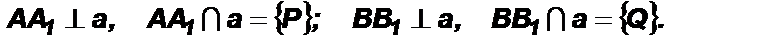
Доказать: 
| a |
| B1 |
| B |
| Q |
| P |
| A1 |
| A |
1) Допустим, что 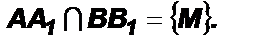 Мысленно перегнем чертеж по прямой а так, чтобы верхняя часть чертежа наложилась на нижнюю.
Мысленно перегнем чертеж по прямой а так, чтобы верхняя часть чертежа наложилась на нижнюю.
2) Так как  то
то 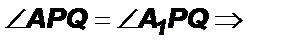 луч РА наложится на луч РА1. Аналогично луч QB наложится на луч QB1.
луч РА наложится на луч РА1. Аналогично луч QB наложится на луч QB1.
3) Если 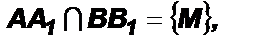 то эта точка наложится на некоторую точку М1, также лежащую на прямых АА1 и ВВ1, т. е.
то эта точка наложится на некоторую точку М1, также лежащую на прямых АА1 и ВВ1, т. е. 
4) Тогда через две точки М и М1 проходят две прямые АА1 и ВВ1, что противоречит аксиоме существования прямых. Следовательно, прямые АА1 и ВВ1 не пересекаются, а значит, 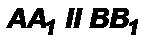 по определению параллельных прямых.
по определению параллельных прямых.
Признаки параллельности прямых.
Теорема 1. Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны.
| b |
| O |
| H1 |
| H |
| B |
| B |
| A |
| A |
| b |
| a |
| a |
Доказательство: Пусть при пересечении прямых a и b секущей АВ внутренние накрест лежащие углы равны. Докажем, что a II b.
1) Пусть 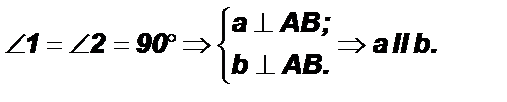
2) Пусть 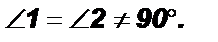 Проведем
Проведем 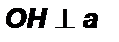 через середину отрезка АВ. На прямой b от точки В отложим отрезок BH1 = AH. Проведем отрезок ОH1.
через середину отрезка АВ. На прямой b от точки В отложим отрезок BH1 = AH. Проведем отрезок ОH1.
3) Рассмотрим ∆AHO и ∆BH1O.
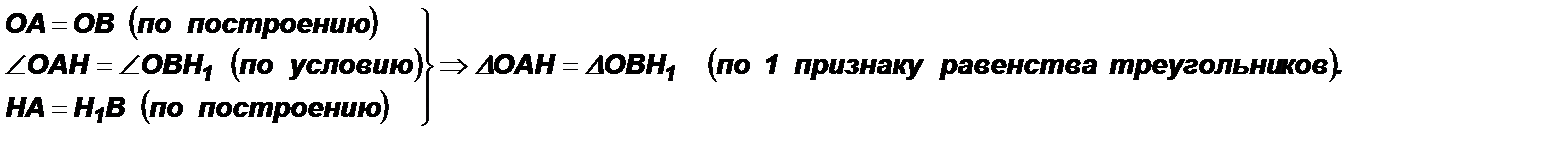
4) Из  5) Из
5) Из 
6) Из  7)
7) 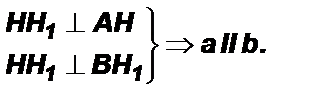
| a |
| c |
| b |
Дано: 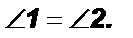
Доказать: 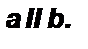
Доказательство: 1) 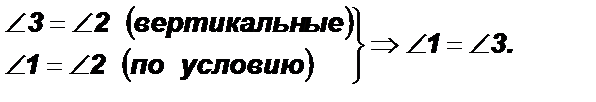
2) 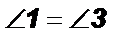 и являются внутренними накрест лежащими
и являются внутренними накрест лежащими 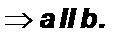
Теорема 3. Если при пересечении двух прямых третьей сумма односторонних углов равна 180°, то прямые параллельны.
Дано: 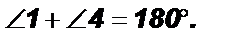 Доказать:
Доказать: 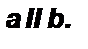
Доказательство:
1) 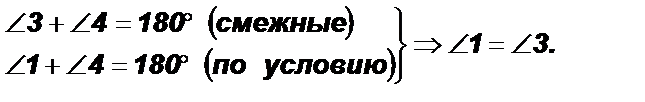
2) 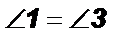 и являются внутренними накрест лежащими
и являются внутренними накрест лежащими 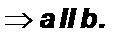
Теорема 4 (об углах с соответственно параллельными сторонами). Если стороны одного угла соответственно параллельны сторонам другого угла, то такие углы или равны или в сумме составляют 180°.
| K |
| Р |
| K |
| Р |
| В1 |
| А1 |
| А |
| В |
| O1 |
| O |
| O |
| O1 |
| В |
| В1 |
| А1 |
| А |
 Доказать:
Доказать: 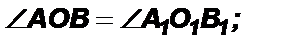
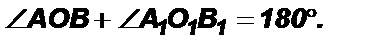
Доказательство:
1) Если 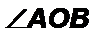 - развернутый, то
- развернутый, то  тоже развернутый. У развернутого угла стороны являются дополнительными полупрямыми и образуют одну прямую.
тоже развернутый. У развернутого угла стороны являются дополнительными полупрямыми и образуют одну прямую.
2) Пусть 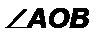 - неразвернутый. Тогда возможны следующие случаи взаимного расположения этих углов:
- неразвернутый. Тогда возможны следующие случаи взаимного расположения этих углов:
Случай 1. (см. рисунок 1).
Продолжим непараллельные стороны углов до пересечения: 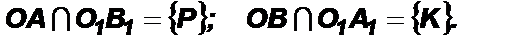

Случай 2. (см. рисунок 2).
Продолжим непараллельные стороны углов до пересечения: 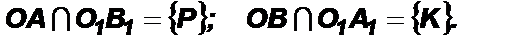

4.Сумма величин внутренних углов треугольника и многоугольника следствие.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 656; Нарушение авторских прав?; Мы поможем в написании вашей работы!