Аналогично доказывается параллельность других прямых

Теорема Фалеса. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные между собой отрезки и на другой его стороне.

B

O

E

A₃

A₂

A₁

B₃

B₂

B₁

F

A

Дано: ÐAOB;

A₁B₁ II A₂B₂ II A₃B₃;

A₁A₂ = A₂A₃.

Доказать: В₁В₂ = В₂В₃.

Доказательство:

1. Дополнительное построение: Через точку В₂ проведем прямую FE II OA, такую, что

2. Полученные четырехугольники FA₁A₂B₂ и ЕA₃A₂B₂ являются параллелограммами по определению (противоположные стороны попарно параллельны). По свойству параллелограмма:

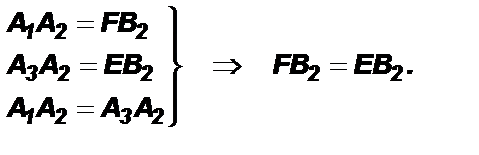
3. Рассмотрим ∆ FB₁B₂ и ∆В₂B₃Е.

4. Из ∆ FB₁B₂ = ∆В₂B₃Е Þ B₁B₂ = В₂B₃.

Замечание: В условии теоремы Фалеса вместо сторон угла можно взять любые две прямые, при этом заключение теоремы будет то же.

B

O

A₃

A₂

A₁

B₃

B₂

B₁

A

Обобщенная теорема Фалеса. Параллельные прямые, пересекающие две данные прямые и отсекающие на одной прямой равные отрезки, отсекают равные между собой отрезки и на другой прямой.

Обратная теорема Фалеса. Если на одной стороне угла от его вершины отложены равные отрезки ОА₁, A₁А₂, A₂А₃,... и на другой его стороне также отложены соответственно равные отрезки ОВ₁, В₁B₂, B₂В₃, то прямые A₁В₁, А₂B₂,... параллельны.

Дано: ÐAOB; B₁B₂ =В₂B₃=…;

A₁A₂ = A₂A₃=….

Доказать: А₁В₁ II A₂В₂….

Доказательство:

1. DOA₁B₁~ DOA₂B₂ (по пропорциональным сторонам и углу между ними).

ÐO-общий. 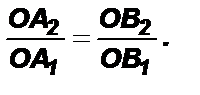OA₂ = OA₁ + A₁A₂ = 2OA₁; OB₂ = OB₁ + B₁B₂ = 2OB₁.

2. Из подобия треугольников следует: ÐOA₁B₁ = Ð OA₂B₂ – соответственные Þ A₁B₁ II A₂B₂.

Определение 1. Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.

Свойство средней линии треугольника. Средняя линия треугольника параллельна основанию треугольника и равна его половине.

Р

D

N

C

B

M

А

Дано: DABC; MN, ND, MD – средние линии.

Доказать: MN II AC;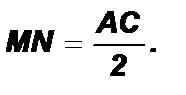

Доказательство:

1. Продолжим MN за точку N и на продолжении отложим PN = MN.
2. Рассмотрим DMBN и DNPC. BN = NC (по определению средней линии);

MN = NP (по построению); ÐMNВ = ÐPNC (вертикальные); Þ DMВN = DNPC (по 1 признаку).

1. ÐBMN = ÐNPC (внутренние накрест лежащие) Þ АВ II PC.
2. CP = MB (из равенства треугольников); AM = MB (по определению средней линии); Þ CP = АM.

5. АM II PC; AM = PC Þ AMPC – параллелограмм Þ AC = MP; AC II MP.

6. MP = 2MN (по построению) Þ MN = 0,5AC.

7. AC II MP; MNÌMP; Þ MN II AC.

14. Трапеция. Свойство средней линии трапеции.

Определение 1. Трапецией называется четырехугольник, две стороны которого параллельны, а две другие – непараллельны.

Параллельные стороны трапеции называются основаниями, а непараллельные стороны – боковыми.

Дата добавления: 2015-04-24