Рассмотрим DNВС и DNDE

Трапеция, боковые стороны которой равны, называется равнобедренной. Трапеция, у которой одна из боковых сторон перпендикулярна основаниям, называется прямоугольной.

Определение 2. Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.

Свойство средней линии трапеции. Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.

E

D

N

C

B

M

А

Дано: ABCD – трапеция; AD II BC; MN – средняя линия.

Доказать: MN II AD; MN II BС;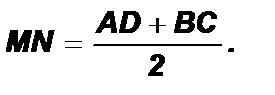

Доказательство:

СN = ND (по условию); ÐВNС = ÐEND (вертикальные);

ÐBСN = ÐNDE (внутренние накрест лежащие при BC II AD и секущей CD);

Þ DNВС и DNDE (по 2 признаку) Þ BN = NE; BC = DE.

Рассмотрим DAВE. MN – средняя линия MN II AD; MN=0,5AE.

AE = AD + DE = AD + BC Þ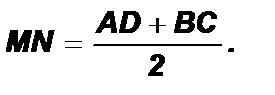

15. Взаимное расположение прямой и окружности.

Прямая и окружность могут находиться в следующих трех относительных положениях:

O

A C E

B D F

K N P

1) Расстояние OР от центра окружности до прямой EF, т. е. длина перпендикуляра, опущенного из центра на прямую, больше радиуса окружности: d > r. Точка Р удалена от центра окружности на расстояние, большее радиуса окружности, и потому лежит вне круга. Для любой другой точки прямой EF расстояние XO > PO > r (наклонные длиннее перпендикуляра), а значит, все точки прямой EF лежат вне круга; значит, прямая не имеет никаких точек, общих с окружностью.

2) Расстояние OK от центра окружности до прямой AB, т. е. длина перпендикуляра, опущенного из центра на прямую, меньше радиуса окружности: d < r. Точка K лежит внутри круга. Прямая AB пересекает окружность, т. е. имеет с ней две общие точки. Прямая OK называется секущей, а ее часть, состоящая из всех точек внутри окружности, является хордой окружности.

3) Расстояние ON от центра окружности до прямой CD, т. е. длина перпендикуляра, опущенного из центра на прямую, равно радиусу окружности: d = r. Точка N принадлежит и прямой, и окружности, все же остальные точки прямой, будучи удалены от О более, чем точка N, лежат вне круга. Значит, в этом случае прямая и окружность имеют только одну общую точку, которая служит основанием перпендикуляра, опущенного из центра окружности на прямую. Такая прямая называется касательной к окружности, а единственная общая точка прямой и окружности называется точкой касания.

16. Доказать свойство касательной окружности. Следствие.

Дата добавления: 2015-04-24