Рассмотрим треугольники СОВ и EOF Свойство 2. Хорды одной окружности равны тогда и только тогда, когда они равноудалены от центра.
Следствие. Расстояние от центра окружности до хорды равно расстоянию от центра до середины хорды.
Угол, вершина которого лежит вне круга и стороны пересекаются с окружностью, измеряется полуразностью двух дуг, заключенных между его сторонами.
18. Доказать теоремы, выражающие свойства хорд и диаметров окружностей.
Свойство 1. Диаметр перпендикулярен хорде, не являющейся диаметром, тогда и только тогда, когда он проходит через середину хорды. Дано: О – окружность; DE – диаметр; АВ – хорда;
АВ ∩ DE = {C}. AC = CB.
Доказать: АВ ^ DE.
Доказательство:
1. Соединим концы хорды АВ с центром окружности. ОА = ОВ = R.
2. Рассмотрим равнобедренный треугольник АОВ. (ОА = ОВ = R). ОС – медиана, проведенная к основанию, по условию (АС = СВ) Þ ОС – высота ОС ^ АВ.
Свойство 1 (обратная теорема). Диаметр, перпендикулярный хорде, не являющейся диаметром, проходит через середину хорды.
Дано: О – окружность; АВ и CD – хорды; OC ^ АВ; OF ^ DE.
Доказать: АВ = DE.
Доказательство:
1. Соединим точки В и Е с центром окружности. ОЕ = ОВ = R.
Свойство 2 (обратная теорема). Если хорды одной окружности равны, то они равноудалены от центра.
Свойство 3. Хорды одной окружности равны тогда и только тогда, когда они стягивают равные центральные углы. Дано: О – окружность; ÐАОВ =ÐDОЕ.
Доказать: АВ = DE.
Доказательство:
1. Соединим концы хорд АВ и DE с центром окружности. OA = OB = ОЕ = ОD = R.
Дата добавления: 2015-04-24 ; Просмотров: 757 ; Нарушение авторских прав? Мы поможем в написании вашей работы!
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет


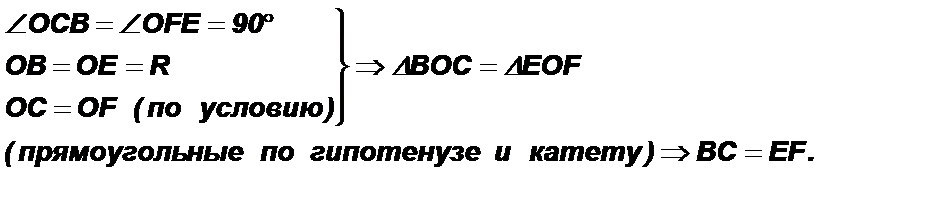 3. BC =EF Þ AB=ED.
3. BC =EF Þ AB=ED.