Дисперсионный анализ и примеры его применения при управлении качеством

Во многих практических ситуациях представляет интерес влия­ние того или иного качественного фактора на рассматриваемый показатель. Влияет ли квалификация наладчиков на качество обработки поверхности? Влияет ли метод обработки на точность изготовления детали? Зависит ли прочность болта из стекловолокнита от температуры при прессовании? Ответ на эти и ана­логичные вопросы дается методами однофакторного дисперси­онного анализа.

Пусть, например, оценка качества поверхности детали про­водится с помощью k приборов и необходимо исследовать, вли­яет ли фактор «прибор» на результат измерений. Если приборов два, то проверка гипотезы о равенстве средних показаний при­боров проводится обычными статистическими методами. Если же приборов больше двух, используются методы дисперсионного анализа. Проверяется нулевая гипотеза Н₀: m₁ = m₂ =... = m_k об отсутствии влияния на результативный признак X (результат измерений) фактора А («прибор»), имеющего k уровней A_j, j=1, 2, …, k..

Основная идея дисперсионного анализа состоит в том, что­бы сопоставить дисперсию за счет воздействия фактора А с дис­персией, обусловленной случайными причинами. Если разли­чие между ними несущественно, то влияние фактора А на признак X незначительно. Если же различие между факторной и оста­точной дисперсиями значимо, то это говорит о влиянии факто­ра А на рассматриваемый признак X.

Предполагается, что случайная величина X имеет нормаль­ное распределение с математическим ожиданием m_j, зависящим от уровня фактора A_j, и постоянной дисперсией σ². В качестве исходных данных используются выборочные значения величины X, полученные для каждого уровня фактора А; число элемен­тов выборки на каждом уровне равно n, тогда общее число на­блюдений nk, обозначим через x_ij результат i-го наблюдения (i=1, 2,..., n) за j-м фактором.

Выборочное среднее, соответствующее j-му уровню фактора А (групповое среднее), вычисляется по формуле

а общее среднее

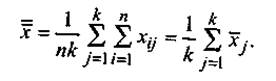
Общая сумма квадратов — это сумма квадратов отклонений наблюдаемых значений х_ij, от общего среднего:

Факторная сумма квадратов (обусловленная влиянием фак­тора А) — это сумма квадратов отклонений групповых средних от общей средней:

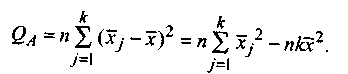
Остаточная сумма квадратов характеризует рассеяние внут­ри группы:

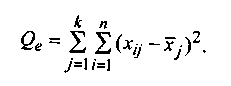
На практике эта сумма определяется из основного тождества дисперсионного анализа, в соответствии с которым

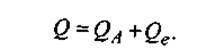
Соответствующие числа степеней свободы

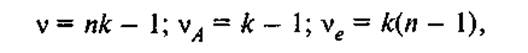
а дисперсии

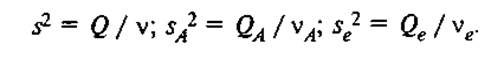
Если нулевая гипотеза о равенстве средних справедлива, то эти дисперсии являются несмещенными оценками дисперсий генеральной совокупности. Значительное превышение диспер­сии S_A² над дисперсией S_e² можно объяснить различием средних в группах. Поэтому для проверки нулевой гипотезы использует­ся отношение этих средних — статистика по формуле

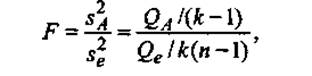
которая имеет распределение Фишера с числами степеней сво­боды (k — 1) и k(n — 1). Нулевая гипотеза не противоречит ре­зультатам наблюдений на заданном уровне значимости α, если

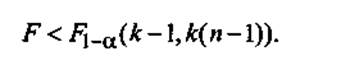
В этом случае считается, что фактор А не оказывает существенного влияния на показатель X. Результаты расчета сводятся в табл.1.

Таблица 1

Дата добавления: 2015-04-24