Непрерывность некоторых функций

Непрерывность функции в точке. Основные понятия. Непрерывность элементарных функций

Бесконечно малые и бесконечно большие функции. Теорема о замене функции эквивалентными при вычислении пределов

Первый и второй замечательные пределы

Первый замечательный предел равен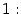

Второй замечательный предел

Теорема lim(1+1/x)^x=e

^x®+¥

Доказательство: Пусть n – целая часть х – n=[x] n£x<n+1

[1+1/(n+1)]ⁿ£(1+1/x)^x£(1+1/n)ⁿ⁺¹

Если x®+¥, то n®+¥

[1+1/(n+1)]ⁿ⁺¹1/[1+1/(n+1)]£(1+1/x)^x£(1+1/n)ⁿ(1+1/n) Þ lim(1+1/x)^x=e

Функция α(x), определенная в ·

O

(x 0), называется бесконечно малой функцией при x → x0, если lim α(x) = 0.

Если lim (a(x)/b(x))=1 при х=>x0 a,b-бесконечно малые ф-ции

то α(x) и β(x) называются эквивалентными бесконечно малыми функциями:

α ~ β при x → x0.

Теорема. Предел отношения двух бесконечно малых функций не изменится, если каждую функцию (или только одну из них) заменить на эквивалентную, т.е. если α(x) ~ α1(x) и β(x) ~ β1(x), то lim (a/b)=lim(a1/b1) при х=>x0

Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.

1) y=c (постоянная) непрерывна в "х₀Î R lim c=c. Зададим "ε>0 рассмотрим разность |f(x)-f(x₀)|=|c-c|=0<ε ^x®x_°

" x: |x-x₀|<d ("d>0)!

2) y=x непрерывна в " x₀Î R, то есть lim x=x_0. Зададим "ε>0 рассмотрим разность |f(x)-f(x₀)|=|x-x₀|<ε

^x®x_°

" x: |x-x₀|<d ("d>0)! Þd=ε!

Следствие.

Многочлен p(x)=a_nxⁿ+ a_n-1x^n-1+…+a₁x+a₀

(a_n,a_n-1…a₁,a₀ – зададим число)

n=0,1,2,3…. непрерывен в любой точки х₀ оси как сумма произведения непрерывной функции. Рациональная функция:

R(x)=p(x)/q(x). Частная двух многочленов непрерывна в любой точки х₀ в которой q(x)¹0

Функция f (x), определенная в некоторой окрестности точки a, называется непрерывной в этой точке, если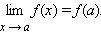

Дата добавления: 2015-04-24