Геометрический и физический смысл производной

Геометрический смысл производной:

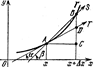Пусть на интервале (а,b) задана непрерывная функ­ция у=f(x). Её график наз. непрерывной кривой. Обозначим его через Г. Зададим на Г точку А = (х,f(х))(рис)

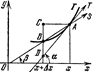и поставим целью определить касательную к Г в этой точке. Для этого введем на Г другую точку B=(x+Dx,f(x+Dx)), где Dx¹0 (рис. 1 изобра­жён случай Dx>0, а на рис. 2 – случай Dx<0). Пря­мую, проходящую через точки А и В, направленную в сторону возрастания х (отмеченную стрелкой), наз. секущей и обозначим через S. Угол, который S образует с положительным направлением оси х, обозначим через b. Мы считаем, что –p/2<b< p/2. При b>0 угол отсчи­тывается от оси x против часовой стрелки, а при b<0 по часовой стрелке. На данных рисунках b>0. На рис. 1 Dx=AC, Dy=СВ, а на рис. 2 Dx=–AC, Dy=–СВ, В обоих случаях Dy/Dx=tgb.

Если Dx®0, то Dy®0 и точка В, двигаясь по Г, стремится к A. Если при этом угол b стремится к некоторому значению a, отличному от p/2 и –p/2, то суще­ствует предел lim_Dx®0Dy/Dx=lim_b®atgb=tga [1], равный производной (конечной) от f в точке x: f'(x)=tga [2]. Обратно, если существует (конечная) производная f'(x), то b®a=arctg f'(x). При стремлении b к a секущая S стремится занять положение направленной прямой Т, проходящей через точку А и образующей угол a с положительным направ­лением оси х. Направленная прямая Т наз. касательной к кривой Т в её точке А. Определение: Касательной к кривой Г (y=f(x)) в её точке А=(х,f(х)) наз. направленная пря­мая Т, к которой стремится секущая S (направленная в сторону возрастания х прямая), проходящая через А и точку В=(x+Dx,f(x+Dx))ÎГ, когдаDx>0. Мы доказали, что если непрерывная, функция у=f(х) имеет конечную производную f'(х) в точке х, то её гра­фик Г в соответствующей точке имеет касательную с угловым коэффициентом tga=f'(х) (–p/2<a<p/2). Обратно, существование предела limb=a(–p/2<a<p/2)

влечет за собой существование конечной производной f'(х) и справедливость равенств (1), (2). Может случиться, что f имеет в точке х правую и левую производные, отличные между собой: f'(x)¹f'_пр(x).

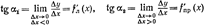
Тогда А есть угловая точка Г. В этом случае касательная к Г в A не существует, но можно говорить, что суще­ствуют правая и левая касательные с разными угловыми коэффициентами:

Дата добавления: 2015-04-24