Производная функции, заданной неявно

Произвожная обратной функции

Пусть функция у=f(х) строго возрастает, непрерывна на интервале (а,b) и имеет конечную не равную нулю производную f'(х) в некоторой точке хÎ(a,b). Тогда об­ратная для f функция х=f^–1(у)=g(y) также имеет производную в соответствующей точке, определяемую ра­венством g'(y)=1/f'(x) [1] или x'_y=1/y'_x [1'] Доказательство: Как нам известно, обратная функция x=g(y) строго возрастает и непрерывна на интервале (A,В), где A=inf f(x), В=sup f(x)

^{xÎ( a ,b) xÎ( a ,b)}

(По теореме о обратной непрерывной функции: Пусть функция f непрерывна и строго возрастает на (a,b) (или на [a,b), или (a,b]) и a=inf f(x), b=sup f(x)

^{xÎ(a,b) xÎ(a,b)}

Тогда образ интервала (a,b) (соответственно [a,b), (a,b]) есть интервал (a,b) (соответственно [a,b), (a,b]) и обратная к f функция x=g(y) однозначна, строго возрастает и непрерывна на (a,b) [a,b), (a,b])). Дадим рассматриваемому у приращение Dy¹0. Ему соответствует приращение Dx обратной функции, также не равное нулю в силу строгой монотонности f. Поэтому Dx/Dy=1/(Dy/Dx). Если теперь Dy®0, то в силу непрерывности g(y) при­ращение Dx также ®0; но при Dх®0 Dy/Dx®f'(x)¹0, =>, существует предел lim_Dy®0Dx/Dy=1/(lim_Dy®0Dy/Dx)=1/f'(x). Этим формула [1] доказана. Примечание: Если f'(x)¹0 непрерывна на (a,b), то g'(y) непрерывна на (A,B). Это следует из [1], где можно положить x=g(y): g'(y)=1/f'[g(y)] (yÎ(A,B)). Ведь сложная функция f'[g(y)], состоящая из непрерывных функций f' и g, непрерывна.

Уравнение вида F(x.y)=0, содержащее переменные x и y, иногда можно разрешить относительно y и получить в явном виде зависимость y=y(x).

Рассмотрим функцию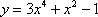

Мы видим, что слева у нас одинокий «игрек» (функция), а справа – только «иксы». То есть, функция в явном виде выражена через независимую переменную

Рассмотрим другую функцию:

Здесь переменные и расположены «вперемешку». Причем никакими способами невозможно выразить «игрек» только через «икс». В курсе математического анализа доказано, что неявная функция существует (однако не всегда), у неё есть график (точно так же, как и у «нормальной» функции). У неявной функции точно так же существует первая производная, вторая производная и т.д.

Найти производную от функции, заданной неявно:

1) На первом этапе навешиваем штрихи на обе части.т.е. берём произфодную от 2-х частей

2) Используем правила линейности производной

3) Непосредственное дифференцирование.

4) В левой части собираем слагаемые, в которых есть «игрек» со штрихом. В правую часть – переносим всё остальное

5) В левой части выносим производную за скобки

6) И по правилу пропорции сбрасываем эти скобки в знаменатель правой части

Дата добавления: 2015-04-24