Моделирование экономики 1 страница

Следствия

Следствия

·

·

·

·

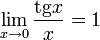
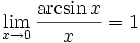
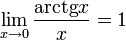
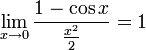
35.Друга важлива границя

или

1.

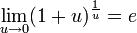
2.

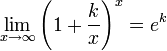
3.

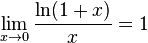
4.

5. для ,

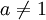
6.

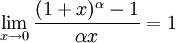
1. Формализация предпочтения потребителя при выборе товаров.

Для получения математической модели задачи потребителя нам нужно формализовать такие понятия как товар, цель потребления товаров, цена товара, бюджет и покупательская способность потребителя.

Мы будем предполагать, что количество каждого товара можно измерять вещественным неотрицательным числом (в штуках, в килограммах, в метрах, в литрах, в человеко-часах и т.д.). Пусть на рынке производится и продается n видов товаров. Вид товара будем обозначать индексом i, так что i=1,…,n. Обозначим через 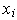количество i -го товара. Вектор будем называть набором товаров. Если в наборе x для некоторых i , то будем говорить, что товар вида i не приобретается данным потребителем. Поэтому множество 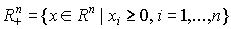будем называть пространством товаров. Заметим, что на количество товаров не накладываются ограничения сверху. Иначе говоря, мы предполагаем, что на рынке существует достаточное количество товаров. Иногда в 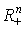выделяется некоторое подмножество Х, как множество реально применяемых товаров, на котором определены интересы данного потребителя. В 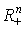наборы товаров можно складывать между собой или умножать на неотрицательное число; в 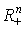вычитание невозможно, если при этом получается отрицательное количество товара. Человек приобретает (покупает) товары с целью максимального удовлетворения своих потребностей. У каждого есть свои вкусы, каждый по своему оценивает пользу или вред от потребления товара. Поэтому потребитель стремится выбрать в пространстве 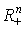"лучший" с его индивидуальной точки зрения товар. При сравнении двух наборов x и y одни предпочтут x, другие - y.

Для того чтобы формализовать выбор потребителя с учетом его цели, в пространстве 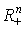определим (индивидуальное) отношение предпочтения, обозначаемое символом 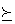. При помощи этого отношения любой набор 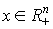можно сравнить с другим набором 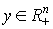. Запись означает, что либо x предпочтительнее чем y, либо наборы x и y для потребителя безразличны (то есть х по крайней мере так же хорош, как и у). Заметим, что в отношении 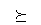набор товаров рассматривается как одно целое (в отличие от векторного неравенства 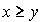, понимаемого покомпонентно).

Строгое предпочтение 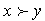имеет место, если и только если , а 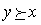несправедливо. Говорят, что наборы х и у безразличны для данного потребителя (обозначают 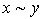) тогда и только тогда, когда и 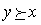. Индивидуальное отношение можно рассматривать как отображение, которое каждому набору 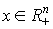ставит в соответствие множество всех тех наборов товаров, которые связаны с х отношением безразличия. Таким образом, отношение безразличия разбивает все пространство 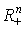на классы эквивалентности (безразличия).

Исходя из логики сравнения товаров, потребуем, чтобы отношение 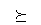удовлетворяло следующим аксиомам:

а₁) рефлексивность: для любого 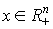справедливо ;
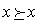а₂) транзитивность: для любого 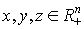, таких, что , 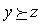справедливо ;
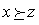а₃) полнота: для любых либо , либо 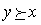, либо .

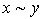Кроме того для отношения безразличия должна иметь место аксиома симметричности: из 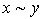следует .

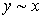Приведем примеры конкретных отношений предпочтения и безразличия.

Пример 3.1. Для сравнения любых наборов предварительно проведем ранжировку (упорядочение) компонентов этих векторов (то есть видов товаров) по важности для данного потребителя: товар вида i важнее, чем товар вида i+1, i=1,…,n-1. После этого определим отношение 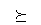следующим образом: , если выполнено одно из n+1 условий:

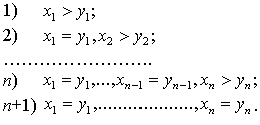
Такое отношение называется лексикографическим предпочтением, так как оно определено по правилу составления списка наименований по алфавиту. Самостоятельно покажите, что отношение лексикографического предпочтения удовлетворяет аксиомам а1), а2), а3).

Пример 3.2. Пусть 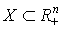, а 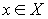такой набор, что для каждого 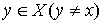найдется хотя бы один индекс i, для которого 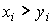. Для такого набора х определим отношение безразличия следующим образом: 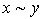, если не имеет место 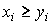для всех i=1,…,n, причем хотя бы одно неравенство строгое.

Это отношение безразличия порождает в Х множество эквивалентности 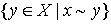называемое множеством Парето.

Отношение предпочтения на практике выявляется экспериментальным путем, сравнивая наборы товаров попарно и спрашивая потребителя, какой набор он предпочитает. Реально такую работу можно провести в случае небольшого числа товаров. Предпочтение потребителя изменчиво и зависит от многих условий: цен товара, его дохода, имеющегося у него запаса товаров, сезона, состояния здоровья, настроения и т.д. Поэтому нельзя раз и навсегда "прикрепить!" за потребителем неизменные принципы предпочтения. Следовательно, при повторном моделировании поведения потребителя его предпочтение нужно формализовать заново "с учетом изменившихся условий". В принципе нет ничего сложного в том, чтобы взять два набора товаров и спросить потребителя, который из них он предпочитает и в результате последовательного опроса найти искомую закономерность. Гораздо сложнее выявить предпочтение целой группы людей или общества, так как невозможно по каждой паре наборов товаров проводить голосование или референдум и ожидать, что результаты будут однозначными. Рассмотрение вопросов "коллективного предпочтения" потребительского сектора мы отложим до пятой главы.

Кроме основных аксиом а1), а2), а3) отношение предпочтения может обладать рядом содержательных свойств. Приведем основные из них:

а₄) непрерывность: для любых 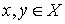множество 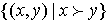является открытым подмножеством декартово произведения 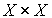(определение открытого множества см. в § 1.2);
а₅) ненасыщаемость: для любых 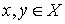неравенство 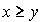влечет 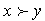и неравенства 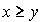, 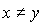влекут ;
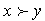а₆) выпуклость: для любых 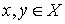отношение влечет 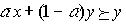, где .

Содержательно непрерывность означает, что если х строго предпочтительнее у, то при малом изменении каждого из них отношение строгого предпочтения сохраняется. Как мы увидим в следующем параграфе, ценность этого свойства заключается в том, что непрерывное отношение предпочтения можно заменить (смоделировать) обычной числовой функцией. Примером отношения предпочтения, которое не обладает свойством непрерывности, является лексикографическое предпочтение (см. Пример 3.1).

Если все товары хорошего качества, то естественно, большее их количество будет предпочтительнее, чем меньшее. Этот факт и отражен в свойстве ненасыщаемости. Оно означает отсутствие такого набора 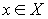, что для всех 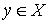(отсутствие точки насыщения).

2. Функция полезности как критерий оценки товаров.

Функция полезности должна быть построена с учетом всех тех объективных и субъективных условий, которые влияют на предпочтение потребителя. Например, полезность денег оценивается не только их покупательской способностью. Так, с большой степенью уверенности можно утверждать, что полезность десяти заработанных долларов больше, чем те же десяти долларов найденных случайно на улице. Для наркомана "полезность" набора товаров тем выше, чем больше в нем содержится героина, а для нормального человека - наоборот. При построении функции полезности все эти нюансы, связанные с понятием полезности, учитываются тем обстоятельством, что эта функция строится сугубо на основе отношения предпочтения, то есть каждому отношению предпочтения соответствует своя функция полезности.

Перейдем к строгим определениям.

Определение 3.1. Пусть в 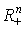определено отношение предпочтения 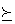. Любая функция 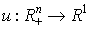такая, что 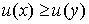тогда и только тогда, когда , называется функцией полезности, соответствующей этому отношению предпочтения.

Если интересы потребителя ограничиваются множеством 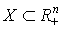, то функция полезности определяется на этом множестве, .

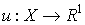В терминах функции полезности отношение безразличия 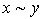задается равенством .

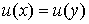Всегда ли можно представить отношение предпочтения функцей полезности? Можно ли исходя из предпочтения 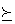найти функцию u, удовлетворяющую определению 3.1? Отвечая на этот вопрос приведем без доказательства следующее утверждение (доказательство можно найти, напр., в [ 18 ]).

Теорема 3.1. Для любого отношения предпочтения, определенного и непрерывного в 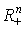, можно построить представляющую его (непрерывную) функцию полезности .

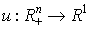Оказывается. что для люього непрерывного отношения предпочтения можно построить целое семейство функций полезности. Этот факт сформулируем в виде следующего утверждения.

Теорема 3.2. Пусть 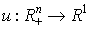- функция полезности, представляющая отношение предпочтения 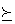. Для любой строго возрастающей функции сложная функция (суперпозиция) 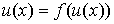является функцией полезности, так же представляющей это отношение предпочтения .

В качестве упражнения, для двух строго возрастающих функций 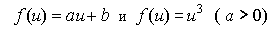проверьте справедливость этой теоремы.

Заметим, что для потребителя все эти функции полезности равнозначны. Он не в состоянии отдать предпочтение одной из них перед множеством возможных других, так как все они отражают одно и то же отношение предпочтения. Различие этих функций касается различных "масштабов" измерения полезности и не является принципиальным.

Так как функция полезности должна быть адекватной отношению предпочтения, то для нее можно сформулировать свойства а₄), а₅), а₆). Например, в терминах функции полезности свойство ненасыщаемости читается так:

a^'₅) для любых 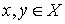неравенство 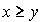влечет неравенство 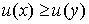и неравенства 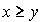, 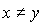влекут .

Из этого определения видно, что в случае ненасыщаемости функция u не достигает своего максимума на множестве Х: для любого 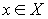найдется 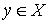, который имеет большую полезность чем х.

Аналогом свойства а₆) является вогнутость функции полезности:

a^'₆) для любых .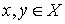

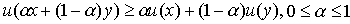Если в условии вогнутости имеет место строгое неравенство, то функция полезности называется строго вогнутой. В этом случае, как будет показано в § 3.3, выбор потребителя определяется однозначно.

Преимущество функции полезности против отношения предпочтения состоит, в частности, в том, что для анализа потребительского выбора можно использовать мощный аппарат дифференцирования.
Пусть функция полезности и дифференцируема и

Частная производная (3.2.1) называется предельной полезностью товара вида i. Это есть полезность, получаемая от "дополнительной" доли товара вида i:

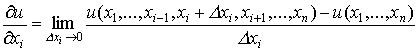
Поэтому неравенство (3.2.1) можно интерпретировать так: для любого набора товаров 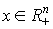возрастание потребления товара вида i при постоянном уровне потребления других товаров приводит к увеличению полезности. Таким образом, (3.2.1) - это условие ненасыщаемости, написанное для дифференцируемой функции полезности. Забегая вперед скажем, что именно предельная полезность товара является определяющим цену товара фактором. Здесь нет противоречия с рыночным механизмом ценообразования, так как при прочих фиксированных условиях спрос на товар определяется его полезностью.

3. Предельный анализ и понятие эластичности в теории потребления.

Рассмотрим произвольный набор товаров 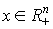. Если полезность от x_i обозначить через 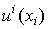, то суммарная полезность набора х есть

Среднюю полезность набора х схематично можно определить как вектор

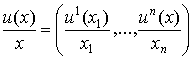
где 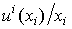- средняя полезность товара вида i, то есть полезность, приходящаяся на единицу товара i. Понятие предельной полезности набора х

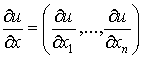
мы уже рассматривали в предыдущем параграфе. Вычисляя частное производное 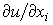, можно получить ответ на вопрос: как себя поведет полезность 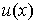при изменении объема потребления того или иного товара. Полезность товара растет, пока справедливо условие (3.2.1). Если с ростом потребления товара неравенство (3.2.1) переходит в обратное, то очевидно, нет смысла и дальше увеличивать его потребление. Поэтому представляет интерес случай, когда 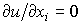. К этому вопросу мы вернемся в следующем параграфе при выявлении оптимальных объемов потребления товара.

Сравнивая среднюю и предельную полезности, можно обнаружить тенденцию средней полезности "стремиться" к предельной полезности. А именно, среднее значение полезности возрастает (при возрастании потребления), если оно ниже предельной полезности; среднее значение полезности остается постоянным (при изменении потребления), если оно равно значению предельной полезности; среднее значение полезности убывает (при возрастании потребления), если оно превосходит предельную полезность.

Сравним среднюю и предельную полезности для разных функций полезности из предыдущего параграфа.

Средняя полезность набора товаров, обладающего свойством замещения (см. (3.2.3)), равна

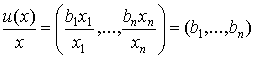
где b_i – средняя полезность товара вида i. Предельная полезность есть

Следовательно, для функции (3.2.3) средняя и предельная полезности совпадают. Этот факт является следствием линейности функции u. Подтверждением служит функция полезности для взаимодополняющих друг друга товаров (см. (3.2.4)):

Для функции Кобба-Дугласа (3.2.8), полагая для простоты n=2, имеем:

С учетом условия 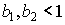ясно, что предельная полезность пропорциональна средней и всегда меньше ее.

Читателю предлагается самостоятельно провести сравнительный анализ средней и предельной полезностей для функций (3.2.9) - (3.2.12).

Предельную величину, как и среднюю, можно считать относительной величиной. Пусть значение некоторой переменной z изменилась от z₁ до z₂. Разницу 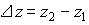называют абсолютным изменением z, а отношение 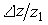- относительным изменением z (изменение, приходящееся на одну единицу исходной величины). В отличие от абсолютного относительное изменение есть величина безымянная. Число называется процентным изменением z.

При помощи предельных величин можно формализовать понятие эластичности, играющую важную роль при анализе взаимосвязи между экономическими показателями и факторами.

Эластичность (коэффициент эластичности) является численной оценкой относительного изменения экономического показателя под действием относительного изменения некоторого экономического фактора при неизменности других влияющих на этот показатель факторов. Таким образом, эластичность показателя - это его чувствительность к изменению влияющего на него фактора.

Возникает естественный вопрос: зачем нужно вводить сложное понятие "эластичность", когда те же изменения можно описать предельными величинами? Как то: изменение полезности от объема потребления товара (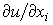), изменение предложения (y_i) от его цены 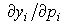- и т.д. Дело в том, что предельные величины, (как и средние) зависят от единицы измерения. Например, величина 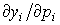в кг./руб. есть одно число, а та же величина в тонна/руб. - другое. Такая неоднозначность приводит к техническим неудобствам. Эта проблема снимается, если чувствительность экономического показателя измеряется эластичностью, так как последняя определена как безымянная величина.

Пусть имеется некоторый экономический показатель z, зависящий от ряда факторов 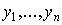, то есть 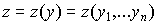. Эластичность показателя z по y_i обозначим 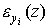и выведем общую формулу для ее вычисления.

По определению эластичности

Переходя к пределу в правой части при , получим

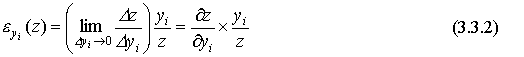
Видим, что "эластичность z по y_i " вычисляется как произведение "предельной величины z по y_i " на "среднюю величину y_i по z ".

Умножая числитель и знаменатель дроби (3.3.1) на 100%, получим

Отсюда, эластичность z по y_i есть отношение процентного изменения z на процентное изменение y_i.

Интересно узнать, насколько процентов изменится z, если y_i изменится на 1%? Иначе говоря, нужно найти процентное изменение z при процентном изменении y_i, равном единице, то есть . Тогда из (3.3.3) сразу получаем искомое процентное изменение:

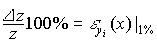
Отсюда, эластичность z по y_i есть процентное изменение показателя z при изменении фактора y_i на 1%.

Как видно из (3.3.2), знак эластичности в каждой точке y зависит от знаков и 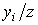. Предположим для простоты, что 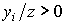. Тогда, если z возрастает по y_i (в точке y), тогда и эластичность положительна; если z убывает по y_i, тогда 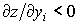и эластичность отрицательна. В этом смысле представляет интерес случай, когда 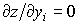, анализ которого и его содержательную интерпретацию мы оставим читателю.

Пороговым значением для эластичности является число 1. Для объяснения этого рассмотрим графическое изображение эластичности функции спроса (с) на один товар, зависящей только от его цены: c=c(p). Известно, (см. рис. 1.2) что спрос является убывающей функцией цены. Вычислим эластичность 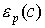в произвольной точке A(p,c) графика функции c=c(p) (рис. 3.2). 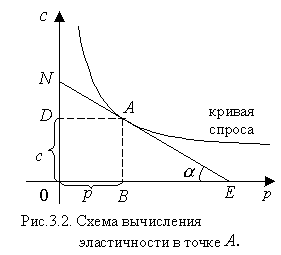Пресечение касательной в точке А с осями координат обозначим через Е и N. По определению

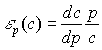
Выразим правую часть равенства через элементы графика. Из

имеем

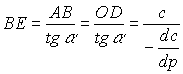
Дата добавления: 2015-04-24