Моделирование экономики 4 страница

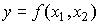
1. Производственная функция Кобба-Дугласа. Первый успешный опыт построения производственной функции, как уравнения регрессии на базе статистических данных, был получен американскими учеными - математиком Д. Коббом и экономистом П. Дугласом в 1928 году. Предложенная ими функция изначально имела вид:

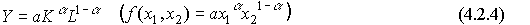
где Y - объем выпуска, K - величина производственных фондов (капитал), L - затраты труда, 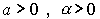- числовые параметры (масштабное число и показатель эластичности). Благодаря своей простоте и рациональности, эта функция широко применяется до сих пор и получила дальнейшие обобщения в различных направлениях. Функцию Кобба-Дугласа иногда мы будем записывать в виде

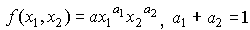
Легко проверить, что 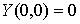и

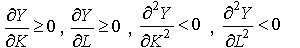
Кроме того, функция (4.2.4) линейно-однородна:

.

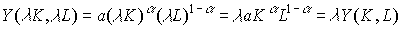Таким образом, функция Кобба-Дугласа (4.2.4) обладает всеми вышеуказанными свойствами.

Для многофакторного производства функция Кобба-Дугласа имеет вид:

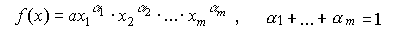
Для учета технического прогресса в функцию Кобба-Дугласа вводят специальный множитель (технического прогресса) 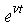, где t - параметр времени, 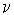- постоянное число, характеризующее темп развития. В результате функция принимает "динамический" вид:

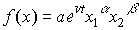
где не обязательно 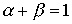. Как будет показано в следующем параграфе, показатели степени в функции (4.2.4) имеют смысл эластичности выпуска по капиталу и труду.

1. Производственная функция CES (с постоянной эластичностью замещения) имеет вид:

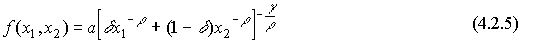
где 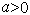- коэффициент шкалы, 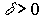- коэффициент распределения, 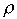- коэффициент замещения, 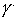- степень однородности. Если выполнены условия

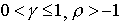
то функция (4.2.5) удовлетворяет неравенствам (4.2.2) и (4.2.3) (проверьте это самостоятельно). С учетом технического прогресса функция CES записывается:

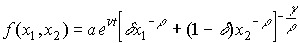
Название данной функции следует из того факта, что для нее эластичность замещения постоянна (см. §4.3).

1. Производственная функция с фиксированными пропорциями. Эта функция получается из (4.2.5) при 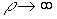и имеет вид:

1. Производственная функция затрат-выпуска (функция Леонтьева) получается из (4.2.6) при :

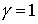Содержательно эта функция задает пропорцию, с помощью которой определяется количество затрат каждого вида, необходимое для производства одной единицы выпускаемой продукции. Поэтому в литературе часто встречаются другие формы записи:

или

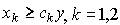
Здесь 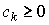- количество затрат вида k, необходимое для производства одной единицы продукции, а y - выпуск.

1. Производственная функция анализа способов производственной деятельности. Данная функция обобщает производственную функцию затрат-выпуска на случай, когда существует некоторое число (r) базовых процессов (способов производственной деятельности), каждый из которых может протекать с любой неотрицательной интенсивностью. Она имеет вид "оптимизационной задачи"

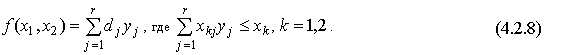
Здесь 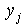- выпуск продукции при единичной интенсивности j -го базового процесса, 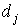- уровень интенсивности, 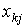- количество затрат вида k, необходимых при единичной интенсивности способа j. Как видно из (4.2.8), если выпуск, произведенный при единичной интенсивности и затраты, необходимые на единицу интенсивности, известны, то общий выпуск и общие затраты находятся путем сложения выпуска и затрат соответственно для каждого базового процесса при выбранных интенсивностях. Заметим, что задача максимизации функции f по 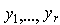в (4.2.8) при заданных ограничениях-неравенствах является моделью анализа производственной деятельности (максимизация выпуска при ограниченных ресурсах).

1. Линейная производственная функция (функция с взаимозамещением ресурсов) применяется при наличии линейной зависимости выпуска от затрат:

где 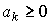- норма затрат k -го вида для производства единицы продукции (предельный физический продукт затрат).

Среди приведенных здесь производственных функций наиболее общей является функция CES. Действительно, как будет показано в §4.3 с применением понятий предельной нормы замещения и эластичности замещения, она обобщает функции Кобба-Дугласа, Леонтьева и линейную производственную функцию.

Исследование функций (4.2.5) - (4.2.9) на предмет соответствия их свойствам 3, 4 и условиям (4.2.2), (4.2.3), предлагается провести читателю самостоятельно.

Для анализа процесса производства и различных его показателей наряду с предельными продуктами,

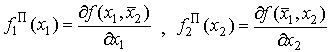
(верхние черточки обозначают фиксированные значения переменных), показывающими величины дополнительных доходов, получаемых при использовании дополнительных количеств затрат, применяются понятия средних продуктов.

Средним продуктом по k -му виду затрат называется объем выпуска, приходящийся на единицу затрат k -го вида при фиксированном уровне затрат других видов:

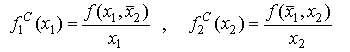
Зафиксируем затраты второго вида на некотором уровне 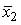и сравним графики трех функций:

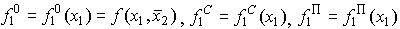
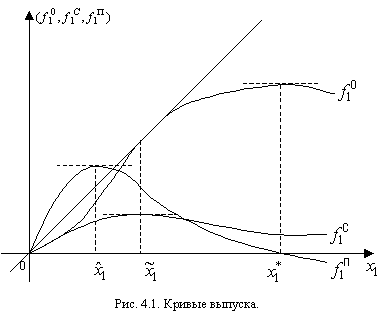
Пусть график функции 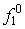имеет три критические точки (как это показано на рис.4.1): 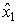- точка перегиба, 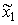- точка касания с лучом из начала координат, 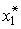- точка максимума. Эти точки соответствуют трем стадиям производства. Первая стадия соответствует отрезку 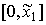и характеризуется превосходством предельного продукта над средним: 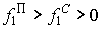. Следовательно, на этой стадии осуществление дополнительных затрат целесообразно. Вторая стадия соответствует отрезку 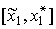и характеризуется превосходством среднего продукта над предельным: 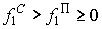(дополнительные затраты не целесообразны). На третьей стадии 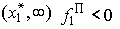и дополнительные затраты приводят к обратному эффекту. Это объясняется тем, что 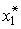является оптимальным объемом затрат и дальнейшее увеличение их неразумно.

Для конкретных наименований ресурсов средние и предельные величины приобретают смысл конкретных экономических показателей. Рассмотрим, например, функцию Кобба-Дугласа (4.2.4), где 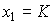- капитал, а 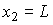- труд. Средние продукты

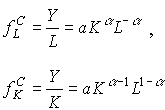
имеют смысл соответственно средней производительности труда и средней производительности капитала (средней фондоотдачи). Видно, что средняя производительность труда убывает с ростом трудовых ресурсов. Это и понятно, так как производственные фонды (K) остаются неизменными, и потому вновь привлекаемая рабочая сила не обеспечивается дополнительными средствами производства, что и приводит к снижению производительности труда. Аналогичное рассуждение верно и для фондоотдачи как функции от капитала.

Для функции (4.2.4) предельные продукты

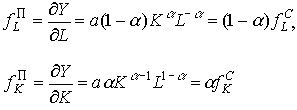
имеют смысл соответственно предельной производительности труда и предельной производительности капитала (предельной фондоотдачи). В микроэкономической теории производства считается, что предельная производительность труда (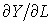) равна заработной плате (цене труда), а предельная производительность капитала (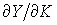) - рентным платежам (цене услуг капитальных благ). Из условия (4.2.2) следует, что при неизменных основных фондах (трудовых затратах) увеличение численности работающих (объема основных фондов) приводит к падению предельной производительности труда (предельной фондоотдачи). Видно, что для функции Кобба-Дугласа предельные продукты пропорциональны средним продуктам и меньше их.

10. Предельный анализ и эластичность в теории производства.

Пояснение сути предельного анализа в экономической теории было дано в §3.3 при изучении теории потребления. Там же были приведены общие определения связанных с ним понятий средних и предельных величин, их относительных и процентных изменений, эластичности и предельной нормы замещения. В этом параграфе речь пойдет о применении этих понятий в сфере производства. Многие методологические аспекты предельного анализа в производстве схожи с теми положениями, которые подробно были изучены в §3.3 для теории потребления. Поэтому здесь изложение материала будет сравнительно лаконичным и сопровождается ссылками к этому параграфу.

Сначала остановимся на понятии эластичности производства. Уже знакомое нам из §4.2 свойство однородности производственной функции оценивает технологию производства в различных точках пространства затрат. А именно, производственная функция в одних точках этого пространства может характеризоваться постоянным доходом от расширения масштаба производства, а в других - его увеличением или, наоборот, уменьшением. Локальным показателем измерения дохода от расширения масштаба производства и служит эластичность производства. Ее мы будем обозначать символом 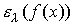("эластичность f по 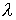в точке x "). Формально (см. (3.3.2)) мы можем написать:

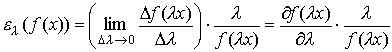
Однако это соотношение не отражает изменение масштаба производства в точке x. Поэтому вычислительная формула эластичности производства выглядит так:

или, что то же самое,

В случае постоянства дохода при расширении масштаба производства (т.е. для линейно-однородной производственной функции) эластичность производства равна единице. Действительно,

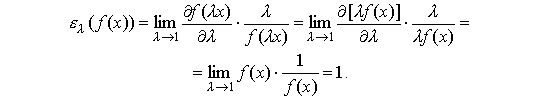
Пример 4.1. Вычислить эластичность производства, описываемого a) функцией Кобба-Дугласа (4.2.4); b) линейной функцией (4.2.9).
Для функции Кобба-Дугласа имеем:

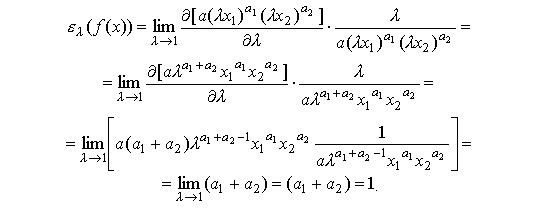
Для линейной производственной функции имеем:

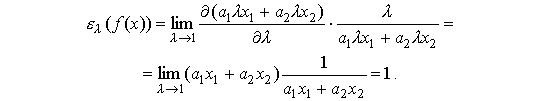
Как легко видеть, здесь мы воспользовались линейной однородностью этих двух функций.

Самостоятельно убедитесь в том, что в случае возрастания (убывания) дохода при изменении масштаба производства его эластичность больше (меньше) единицы. Вычислите эластичность производства, описываемого функциями (4.2.5)-(4.2.8).

Естественно, что предпочтение отдается производству с большей эластичностью, так как увеличивать затраты имеет смысл, если только это приводит к увеличению выпуска. Объективность оценки эластичности производства безусловно зависит от того, насколько адекватно производственная функция, как модель, отражает взаимосвязь затрат с выпуском. Можно говорить, что каждая производственная функция "по-своему" оценивает эластичность производства.

Для практического анализа производства также представляет интерес эластичность выпуска по видам ресурсов как величина, характеризующая процент прироста продукции при увеличении затрат на 1%:

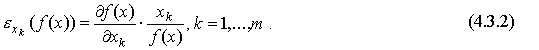
Теорема 4.1. Эластичность производства, описываемого дифференцируемой линейно-однородной функцией, в любой точке пространства затрат равна сумме эластичностей выпуска по всем видам затрат.

Доказательство. Дифференцируя по 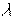обе части равенства 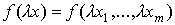по правилу дифференцирования сложной функции, имеем:

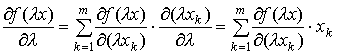
Пользуясь этим равенством, выражение (4.3.1) можно переписать в виде

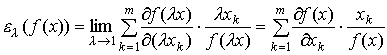
Здесь мы воспользовались линейной однородностью производственной функции f. Теперь ясно, что (см. (4.3.2))

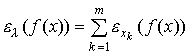
а это и требовалось доказать.

Пример 4.2. Проверить утверждение теоремы 4.1 для производственных функций примера 4.1.
Для функции Кобба-Дугласа имеем:

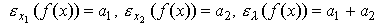
(см. пример 4.1); для линейной функции имеем:

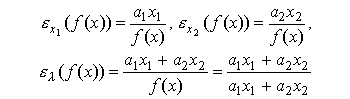
(см. пример 4.1).

На практике по разным причинам часто возникает необходимость замены одних ресурсов другими. Например, при расширении производства фирма должна решить: либо полностью автоматизировать производство за счет дорогостоящего оборудования и сократить количество рабочих мест (сократить фонд заработной платы), либо использовать предназначенные для этого средства для частичной модернизации технологии и увеличения фонда заработной платы. Что выгодно для фирмы? Для получения ответа на этот вопрос вводят понятия предельной нормы замещения одних ресурсов другими и эластичности замещения одних ресурсов другими.

Возможности замещения характеризуют производственную функцию с точки зрения различных комбинаций затрат, порождающих одинаковые уровни выпуска. Предположим, что двухфакторное производство описывается производственной функцией 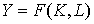, где Y - выпуск, K - капитал (основные фонды), L - трудовые ресурсы. Предположим, часть рабочих (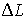) уволилась. На какую величину 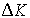следует увеличить основные фонды, чтобы выпуск остался на прежнем уровне, т.е. чтобы имело место равенство 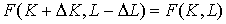? Рассуждая как в §3.3 (см. (3.3.5)-(3.3.10)), получаем, что количество основных фондов надо увеличить на величину

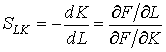
Число 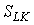называется предельной нормой замещения трудовых ресурсов основными фондами. (Самостоятельно вычислите 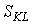и убедитесь, что .)

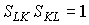Например, для функции Кобба-Дугласа (4.2.4)

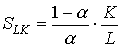
т.е. предельная норма замещения прямо пропорциональна фондовооруженности - чем больше фондовооруженность, тем выше уровень компенсации одной единицы трудовых ресурсов основными фондами.

В общем случае, т.е. для производственной функции 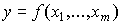, формула для вычисления предельной нормы замещения i -го ресурса k -м ресурсом имеет вид:

Предлагается читателю самостоятельно вычислить предельные нормы замещения и провести их анализ для производственных функций (4.2.5)-(4.2.9).

Из формул (4.3.2) и (4.3.3) вытекает взаимосвязь между эластичностью и предельной нормой замещения: для любых i и k

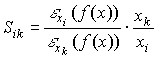
Отсюда, в частности, можно сделать вывод о том, что для тех ресурсов, по которым выпуск неэластичен (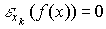), нет смысла говорить о предельной норме замещения ими других ресурсов. Дробь 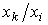, где i - заменяемый, а k - замещающий ресурсы, показывает, сколько единиц замещающего ресурса приходится на одну единицу заменяемого ресурса.

Итак, предельная норма замещения показывает величину ресурса одного вида, которой производитель готов пожертвовать ради одной единицы ресурса другого вида. Поставим теперь "обратный" вопрос: как изменится величина 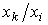при изменении предельной нормы замещения 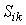на 1%? Согласно определения эластичности, это есть "эластичность 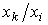по 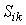". По формуле вычисления эластичности (3.3.2) имеем:

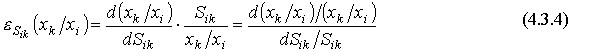
Эта величина называется эластичностью предельной нормы замещения (или просто эластичностью замещения). Введем более простое обозначение 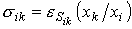. С учетом известной формулы

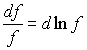
где 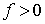, эластичность (4.3.4) можно представить в виде:

Для практики особый интерес представляет случай постоянства эластичности замещения, т.е. независимость отношения 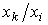от предельной нормы замещения .

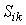Покажем, что таким свойством обладает производственная функция CES (для простоты рассмотрим случай двухфакторного производства (см. (4.2.5)). С этой целью сперва вычислим предельную норму замещения для функции CES:

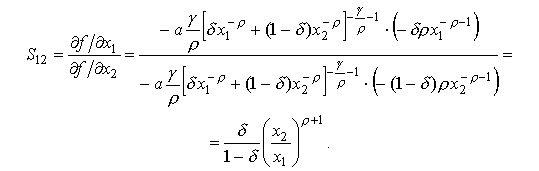
Подставляя это в формулу (4.3.4), получим:

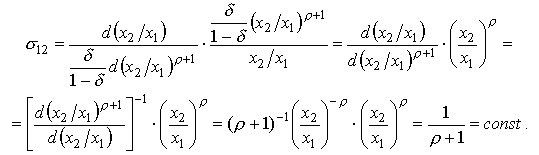
Аналогичным образом можно показать, что 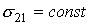и, более того, 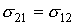(убедитесь в этом). Поэтому эластичность замещения для функции CES можно обозначить просто как 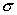. Легко видеть, что

Нулевая эластичность означает отсутствие замещения. В общем, чем больше величина 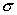, тем шире возможность замещения одних ресурсов другими. Стремление значения 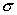к бесконечности означает, что каждый ресурс используется независимо от других.

11. Конструирование и оценка производственных функций.

По существу, производственная функция f есть совокупность "правил", с помощью которых для каждого набора затрат 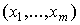определяется соответствующий выпуск y: 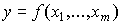. Поэтому построение производственной функции означает нахождение математической формулы, отражающей эти правила или, иначе говоря, закономерности превращения набора ресурсов в конечный продукт. Этот процесс условно можно представить схемой:

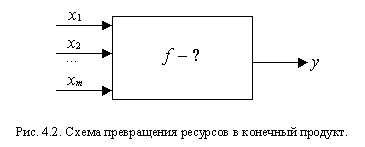
В блоке f (см. рис. 4.2), образно говоря, происходит "смешивание" ресурсов 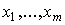в определенных "пропорциях" таким образом, чтобы получился требуемый продукт. Эти "пропорции" определяются спецификой производства и математически выражаются с помощью различных коэффициентов и показателей степени для величин 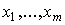. "Смешивание" их математически выражается с помощью разных формальных операций между ними (суммирования, произведения, логарифмирования и т.д.), вид и сочетание которых также определяется спецификой моделируемого производства. Так что вопрос построения производственной функции в каждом конкретном случае сводится к нахождению этих "пропорций" и к определению характера их "смешивания".

Из сказанного выше следует, что для построения производственных функций нужно знать технологию производства, ее структуру и организацию, а также принципы работы сложных машин и оборудования, т.е. надо быть одновременно и технологом, и инженером, и математиком. Оказывается, что знание всего этого сложного производственного механизма не требуется, если владеть подходящими математическими приемами. Речь идет об использовании методов регрессионного анализа (см. §2.5) на основе статистических (опытных, экспертных) данных о затратах и выпуске. Не умаляя достоинства других математических и иных методов построения производственных функций, можно сказать, что именно методы регрессионного анализа наилучшим образом оправдали себя на практике и потому являются наиболее популярными. Поскольку вопросы построения производственных функций на основе экспериментальных данных являются предметом изучения специального раздела - эконометрики, то сами эти методы будут изучаться в главе IX. Здесь же мы коснемся лишь содержательной стороны построения конкретных видов производственных функций.

Идею применения статистических данных для построения производственной функции можно объяснить на рисунке 4.2. Имеются известные величины 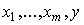(реальные результаты производства) и одно неизвестное выражение f, их связующее. Наблюдая в течение достаточно большого периода времени функционирования производства за различными значениями затрат 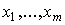и соответствующими им значениями выпуска y, можно выявить закономерность f:

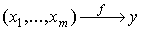
Например, свою знаменитую функцию (4.2.4) Кобб и Дуглас получили на основе изучения статистических данных по расходованию капитала (K), труда (L) и индекса производства (Y) в американской обрабатывающей промышленности за период с 1899 по 1922 гг. Практическая значимость этой функции подтверждается тем, что соответствующая замена исходных данных позволяет использовать ее для анализа любого производства (такую программу на языке Бейсик можно найти в книге [ 14 ]).

Кратко остановимся на этапах построения производственной функции. Пусть нам известны виды ресурсов (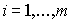), используемых для выпуска данной продукции, и имеется необходимое количество статистических данных по объемам затрат 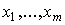и выпуска y. Требуется установить зависимость 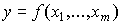, т.е. найти аналитический вид производственной функции f. Эта задача распадается на два этапа:

1. спецификация функции f, т.е. выявление общего вида функции f от аргументов 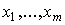с неопределенными параметрами (коэффициентами и показателями степеней при 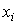и свободным членом);
2. оценка параметров - определение конкретных числовых значений неизвестных параметров.

Картина "расположения" статистических данных в пространстве затраты-выпуск может подсказать линейный или нелинейный характер зависимости функции f от аргументов 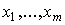. Например, в случае линейной производственной функции результатом спецификации будет гипотеза о линейной зависимости вида

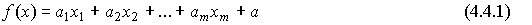
в случае производственной функции Кобба-Дугласа - в виде мультипликативной функции

в случае производственной функции CES - в виде степенного многочлена

и т.д. Здесь 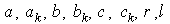являются неизвестными параметрами, подлежащими определению (оценке).

Чаще остальных на практике применяется аппроксимация вида (4.4.1), называемая линейной регрессией.Для определения ее параметров используется (линейный) метод наименьших квадратов. В некоторых случаях к линейной аппроксимации удается свести и нелинейные относительно ресурсов производственные функции. Например, логарифмируя функцию (4.4.2), получим:

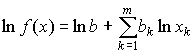
Далее, вводя обозначения

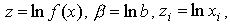
Дата добавления: 2015-04-24