Моделирование экономики 2 страница

(здесь знак минус показывает убывание функции с в точке А). Из подобия треугольников ABE и ADN имеем:

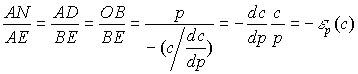
Следовательно,

Можно показать, что для возрастающей функции (напр., предложения, как функции от цены) эластичность по абсолютной величине также будет равна отношению AN/AE. Потому в общем случае эластичность следует оценивать по ее абсолютной величине. Эта величина равна 1, если в (3.3.4) числитель равен знаменателю; больше 1, если числитель больше знаменателя и меньше 1 - если числитель меньше знаменателя. Это говорит о том, что эластичность 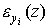зависит от кривизны графика функции z в рассматриваемой точке.

Если 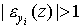, то функция z называется эластичной (по y_i); если 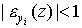, то функция z называется неэластичной (по y_i); если 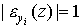, то говорят, что функция z имеет единичную эластичность (по y_i).

Относительно спроса различают товары эластичного спроса и товары неэластичного спроса. Для товаров первого вида повышению цены на 1% соответствует понижение спроса более, чем на 1% и, наоборот, понижение цены на 1% приводит к росту покупок более, чем на 1% (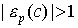). Для товаров второго вида повышение цены на 1% влечет за собой понижение спроса менее, чем на 1% и, наоборот, уменьшение цены на 1% приводит к росту покупок менее чем на 1% (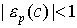). К этому вопросу мы еще раз вернемся в § 3.5 после формализации понятия спроса.

Вычислим эластичность некоторых из функций полезности приведенных в § 3.2 (для простоты будем полагать n=2).

Для функции с полным взаимозамещением благ (3.2.3)

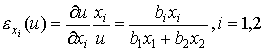
Например, в точке 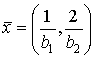получаем:

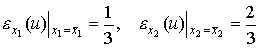
Видим, что в точке 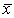полезность в целом неэластична; при этом неэластичность по второму товару "выше", чем по первому товару. Более детальный анализ эластичности функции (3.2.3) оставляем читателю.

Для функции Кобба-Дугласа (3.2.8) имеем:

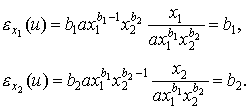
Итак, параметры b₁ и b₂ в функции Кобба-Дугласа как раз являются коэффициентами эластичности по видам товаров; они постоянны, то есть не зависят от объема потребления. Поэтому функция Кобба-Дугласа относится к классу функций полезности с постоянной эластичностью (вернее, неэластичностью, так как ).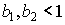

В завершение параграфа рассмотрим еще одно понятие, определяемое с помощью дифференцирования.

Предположим, что имеется шесть наборов товаров

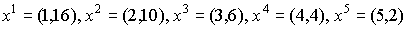
с одинаковой полезности, то есть 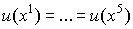. Пусть первый вид товара (i=1) - продукт питания, второй (i=2) -одежда. Эти точки лежат на одной кривой безразличия u(x)=c (рис.3.3). 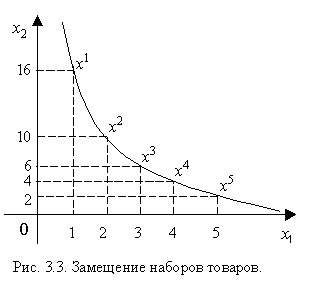Как видно из графика, замена набора x¹ набором x² требует отказа от 6 единиц одежды взамен на одну единицу продукта питания; замена x² на x³ - отказа от 4 единиц одежды ради одной единицы продукта питания и т.д. Чтобы количественно определить объем некоторого товара, которым потребитель готов пожертвовать ради другого товара, используют меру, называемую предельной нормой замещения. Более точно, предельная норма замещения показывает, на сколько единиц нужно уменьшить (увеличить) количество одного товара при увеличении (уменьшении) другого товара на единицу, чтобы при этом полезность осталась неизменной.

Обозначим предельную норму замещения i-го товара j-м товаром через S_ij и выведем формулу для ее вычисления.

Пусть при уменьшении потребления j-го товара на величину 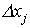для поддержания прежнего уровня полезности необходимо увеличить потребление i-го товара на величину :

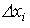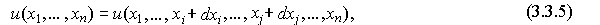
где 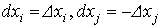. По определению предельной нормы замещения

Из (3.3.5) получаем

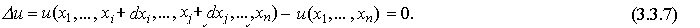
Для полного приращения 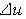функции u в математическом анализе существует формула:

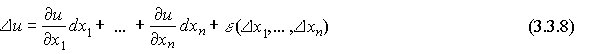
где 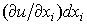-частные дифференциалы, а 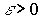таково, что

Выражение

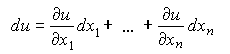
есть полный дифференциал (см. (2.2.4)) функции u. Из (3.3.7)-(3.3.9) с учетом того, что для, имеем

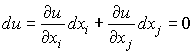
Отсюда

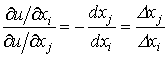
и из (3.3.6) получаем окончательно

Следовательно, предельная норма замещения товаров выражается через отношение их предельных полезностей. Например, для функции Кобба-Дугласа (3.2.8) имеем:

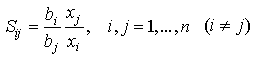
Из закона об убывающей предельной полезности следует выпуклость кривых безразличия (не путать с вогнутостью функции u) (см. (3.2.2)). Поэтому при движении вниз вдоль кривой безразличия (рис. 3.3) S₁₂ убывает:

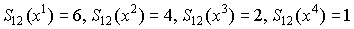
Этот факт в экономике называется законом убывающей предельной нормы замещения: при стремлении поддерживать неизменным уровень полезности путем замещения i-го товара j-м товаром, субъективное удовлетворение, получаемое от предельного потребления i-го товара, в сравнении с удовлетворением, получаемым от предельного потребления товара j, будет неуклонно уменьшаться.

Формы кривых безразличия показывают на разные степени желательности замены одного товара другим. Пусть кривые безразличия для двух различных потребителей относительно напитка (i=1) и сока (i=2) имеют следующий вид (рис. 3.4 и 3.5):

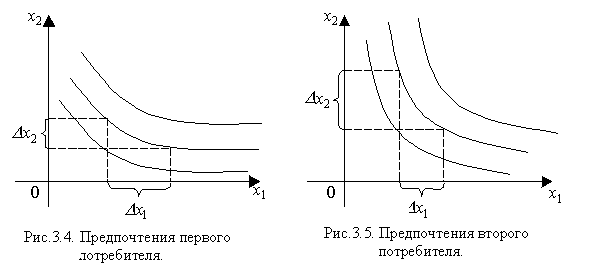
У первого потребителя (рис.3.4) низкая предельная норма замещения напитка соком - он готов отказаться от очень небольшого количества сока ради напитка (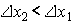). У второго потребителя (рис.3.5), наоборот, высокая предельная норма замещения напитка соком ().

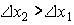4. Оптимизационная модель задачи потребительского выбора.

Пусть
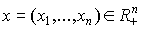- набор товаров, где x_i - количества товара вида i, n - число видов товаров, 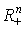- пространство товаров;
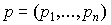- вектор цен товаров, где p_i - цена единицы товара вида i;
K - доход (бюджет) потребителя.

Мы рассматриваем статическую задачу, поэтому эти величины не зависят от фактора времени. Параметры p_i и K считаются постоянными величинами, причем цены считаются рыночными, а доход не структуризуется, то есть нас не интересует из каких частей он складывается. Компоненты x_i вектора являются неизвестными переменными. Модель составляется как раз для определения "оптимальных" значений этих переменных для данного потребителя. Цель потребителя будем описывать с помощью функции полезности 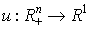(см. § 3.2 и определение 3.1), относительно которой будем предполагать выполнение условий (3.2.1) и (3.2.2). Наконец, мы рассматриваем некоторого "обобщенного" потребителя, никак не характеризуя его индивидуальные особенности, за исключением априорного предложения о существовании функции полезности, отражающей его индивидуальные предпочтения в (см. Теорему 3.1).

С учетом всего сказанного выше, модель задачи потребительского выбора имеет вид:

Обозначим через 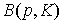множество всевозможных товаров, допустимых потребителю при ценах p и доходе K:

называемое бюджетным множеством. Графическое изображение этого множества показано на рис.3.6.

Граница

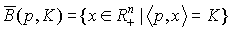
множества 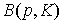называется бюджетной линией.

Оптимальным решением задачи (3.4.1)-(3.4.2) называется такой вектор 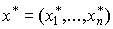, что

Определение 3.3. Оптимальное решение 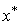задачи (3.4.1) - (3.4.2) называется спросом потребителя.

Данное формальное определение спроса отражает классическое понятие спроса как платежеспособную потребность.

Всегда ли существует оптимальное решение задачи (3.4.1) - (3.4.2)?

Поскольку мы имеем дело с оптимизационной задачей (линейный или нет в зависимости от функции полезности u) (см. § 2.3), то на этот вопрос следует ответить с точки зрения теоремы Вейерштрасса (§ 2.3). Так как функция полезности непрерывна по факту ее существования (см. Теорему 3.1), основная сложность заключается в компактности множества (3.4.3), на котором ищется максимум функции u (см. (3.4.4)). В метрическом пространстве 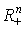, как известно, компактность множества равнозначно его замкнутости и ограниченности (см. § 2.2). Так как бюджетное множество замкнуто по определению, то остается изучить его ограниченность.

Покажем, что ограниченность не всегда имеет место. Предположим, для некоторого i p_i=0. Как следует из (3.4.2), в этом случае "допустимым" становится любой вектор 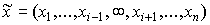, то есть 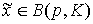, что говорит о неограниченности бюджетного множества. А это, в свою очередь, может привести к отсутствию оптимального решения задачи (3.4.1)-(3.4.2) (напр., в случае неограниченности функции u, что является следствием ненасыщаемости потребителя (см. свойство a^'₅ в §3.2)). Однако, если потребитель ненасыщаем по всем товарам, то множество 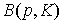оказывается ограниченным. Более строже этот факт сформулирован в следующем утверждении.

5. Функция спроса и ее свойства.

Решение оптимизационной задачи - это лишь один из способов определения спроса, который схематично можно представить так:

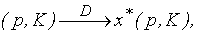
где 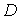- отображение, представленное максимизацией функции u с учетом бюджетного ограничения. В общем случае 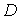- это некоторая совокупность правил, с помощью которых потребитель определяет свой спрос.

Пусть 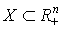- множество допустимых наборов товаров, 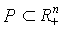- пространство цен. Функцией спроса (индивидуального потребителя) называется отображение 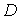, которое каждой паре 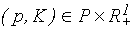ставит в соответствие множество наиболее предпочтительных наборов товаров

где 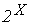- множество всех подмножеств множества X. Это же отображение можно записать как

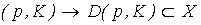
Любая точка 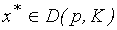называется спросом (при ценах 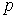и доходе ).

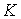Итак, в общем случае функция спроса - это многозначное отображение. Действительно, если 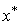- вектор спроса, а множество 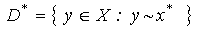не пусто, то любая точка множества 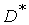является спросом.

Для отображения 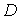, представленного задачей (3.4.1) - (3.4.2), имеем:

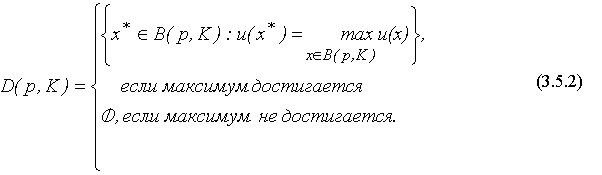
Если в (3.4.1) функция полезности u строго вогнута, то функция спроса 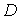однозначна, т.е. множество 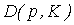состоит из одной точки 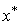максимума функции .

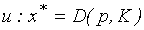В случае неоднозначности функции спроса возникает дополнительная проблема выбора единственной точки 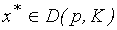. Этот вопрос будет рассмотрен в главе VII.

Принимая во внимание тот факт, что доход потребителя зависит от цен товаров, 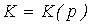, можно в пространстве 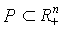определить функцию спроса 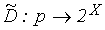, так что .

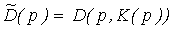При увеличении цен на товары, вообще говоря, доход потребителя должен быть компенсирован. Это требование формализуется как свойство однородности первой степени (или линейной однородности) функции дохода: для любых 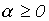. Как должен при этом измениться спрос? Интуитивно ясно, что если повышение цен пропорциональным образом компенсируется повышением дохода, то спрос должен оставаться на прежнем уровне.

Если для любых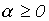

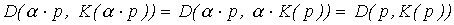
то говорят, что функция спроса однозначна нулевой степени (относительно всех цен и дохода). Это есть инвариантность спроса относительно пропорционального повышения цен и дохода.

Для n функций спроса

полученных как решение задачи (3.4.1) - (3.4.2), это свойство выполнено. Действительно, при изменении цен в 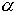раз задача (3.4.1) - (3.4.2) деформируется в следующую:

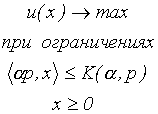
Оптимальной решение этой задачи обозначим 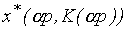. Бюджетное ограничение можно записать как 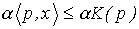. Так как 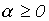, то мы приходим к исходной задаче, так что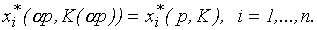

Для функции спроса однородной нулевой степени объем потребления зависит не от цен, как таковых, и дохода, а от отношений цен (относительных цен) и от отношения денежного дохода к цене (реального дохода). Выбирая какой-либо товар, например, товар i=1, в качестве "единицы измерения" (эквивалента) и полагая коэффициент пропорциональности 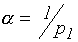, функцию спроса можно записать в виде:

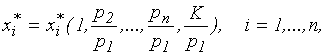
где 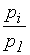- относительная цена, 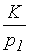- реальный доход. В качестве коэффициента пропорциональности можно выбрать, например, величины

Какова чувствительность спроса 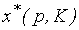на изменение цен и дохода? Как мы видели в § 3.3, она измеряется эластичностью.

Напомним, что эластичность спроса по цене показывает, какое процентное изменение спроса последует за однопроцентным увеличением цены товара:

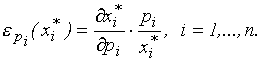
Так как 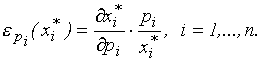(закон спроса для нормальных товаров), 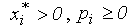, то 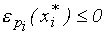(см. также (3.3.4)). Так как при движении по кривой безразличия 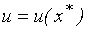величина 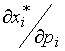меняется (за исключением некоторых тривиальных случаев) и тем более изменяются 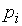и 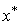, то эластичность спроса по цене в различных точках кривой безразличия различна.

Тривиальным является случай, когда функция спроса линейна:

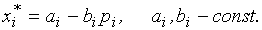
В этом случае 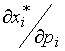постоянна и равна 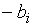, однако, эластичность не постоянна, ввиду непостоянства отношения 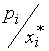. Например (рис. 3.12), в случае одного товара: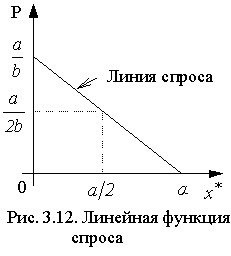

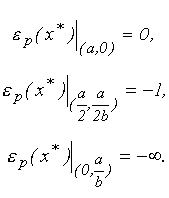
Имеется еще два тривиальных (особых) случая эластичности спроса по цене, показанных на рис. 3.13

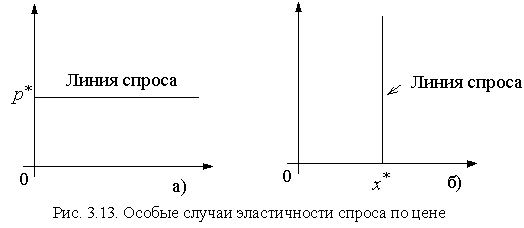
В случае а) - имеется только одна цена , по которой потребитель будет приобретать товар; даже при малейшем увеличении цены выше этого уровня требуемое количество товара упадет до нуля, и любое снижение цены приведет к неограниченному росту спроса. Кривая же спроса, изображенная на рис. 3.13 б) совершенно неэластична. Потребитель приобретет фиксированное количество товара 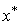независимо от цены.

Координатная запись функции спроса (3.5.3)

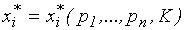
говорит о том, что спрос на один вид товара зависит, вообще говоря, от цен и других товаров.

Процентное изменение количества товара вида i при однопроцентном увеличении цены товара вида 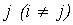называется перекрестной эластичностью спроса по цене:

или

Для взаимозаменяемых товаров (таких, как чай и кофе) повышение цены товара j увеличивает спрос на товар i, поэтому перекрестная эластичность положительна. Для взаимодополняющих друг друга товаров (таких, как кофе и сахар) повышение цены одного товара влечет понижение спроса на другой, поэтому перекрестная эластичность отрицательна.

До сих пор мы говорили о точечной эластичности, т.е. о эластичности, измеряемой в отдельной точке кривой спроса. Если требуется измерение эластичности на отрезке (точнее, на дуге) кривой спроса, то применяют дуговую эластичность спроса по цене:

где

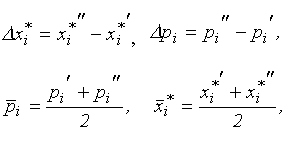
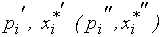- цена и количество товара в начальной (конечной) точке рассматриваемой дуги кривой спроса. Дуговая эластичность тем точнее, чем ближе друг к другу точк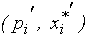и и 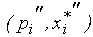. Устремляя расстояние между ними к нулю, очевидно, мы получим формулу точечной эластичности.

Пример 3.5 [ 10 ]. Пусть кривая спроса имеет вид 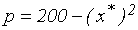. Требуется вычислить эластичность спроса по цене при изменении последней от 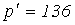до 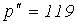(рис. 3.14) 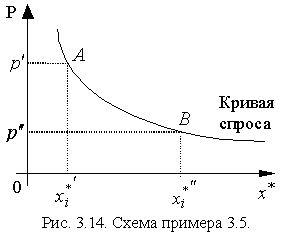Прежде всего, пользуясь формулой спроса, найдем соответствующие этим ценам количества товаров:

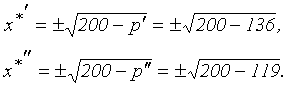
Отбрасывая отрицательные значения корней, как не имеющих смысла, найдем: 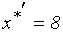, 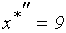. Теперь наша задача сводится к вычислению дуговой эластичности спроса по цене для участка (дуги) кривой спроса 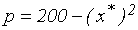от точки A=(136,8) до точки B=(119,9). Пользуясь формулой (3.5.5), получаем:

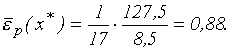
Для сравнения вычислим точечную эластичность в точке A:

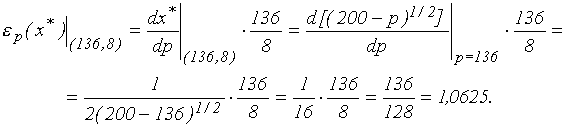
(Здесь мы учли неравенство ).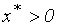

Представляет определенный интерес также эластичность спроса по доходу. Это есть процентное изменение количества требуемого товара (спроса) при однопроцентном изменении дохода:

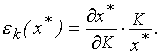
6. Анализ влияния дохода и цен на спрос.

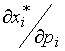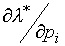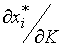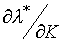Для оценки различных ситуаций в сфере потребления применяются предельный спрос и предельная полезность денег по ценам ( и ) и доходу ( и ). Поэтому желательно иметь формулы для их вычисления. Если общее решение задачи (3.4.1) - (3.4.2) для конкретной функции полезности u найдено в виде функций

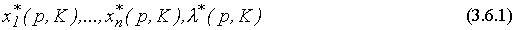
от 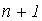параметра 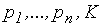, то требуемые предельные величины можно найти, вычисляя частные производные функций (3.6.1) по 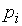и 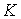. Но эти же предельные величины можно найти не решая задачу (3.4.1) - (3.4.2), а сразу из системы необходимых и достаточных условий оптимальности (3.4.5) - (3.4.8).

Зная теперь, что оптимальное решение 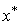задачи (3.4.1) - (3.4.2) лежит на бюджетной линии (см. рис. 3.7), мы можем априори считать, что доход 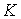будет использован полностью. Тогда в (3.4.2) будет строгое равенство, и система (3.4.5) - (3.4.8) примет вид:

Так как эта система зависит от параметров 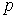, 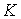и содержит неизвестные 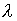, x, то нам удобно ввести обозначения:

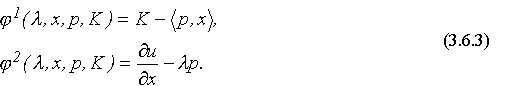
Как и ранее, будем предполагать, что функция u дважды непрерывно дифференцируема и удовлетворяет условиям (3.2.1) - (3.2.2).

Система (3.6.2) будет разрешимой относительно 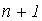переменных 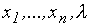, если определитель матрицы Якоби (матрица первых производных системы (3.6.2))

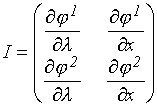
отличен от нуля. Покажем, что это так и есть. С учетом обозначений (3.6.3) получаем:

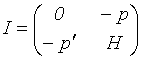
где 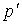- транспонированный вектор 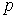, H - матрица Гессе (матрица вторых производных системы (3.6.2)). В координатной форме

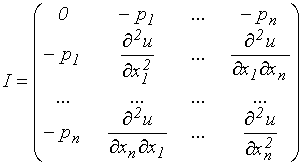
- есть "окаймляющая" ценами товаров матрица Гессе. По условию (3.2.2) матрица Гессе отрицательно определена (см. §2.3) и поэтому невырожденна. Следовательно, определитель матрицы Якоби не равен нулю, и система (3.6.2) имеет решение (по 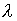и x).

Дата добавления: 2015-04-24