Моделирование экономики 5 страница

приходим к линейной регрессии вида (4.4.1):

Применяя такой способ на основе статистических данных упомянутого выше периода, Кобб и Дуглас получили следующую оценку параметров для своей функции:

и, следовательно, их производственная функция выглядела так:

Дальнейший анализ показал, что за исключением некоторых случаев (например, учета технического прогресса), имеет место соотношение . Так как величина показывает эластичность производства, равенство является признаком линейной однородности производственной функции. Этот факт позволяет записывать функцию Кобба-Дугласа в ви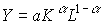де , где .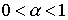

В отличие от функции Кобба-Дугласа, функция (4.4.3) даже после логарифмирования остается нелинейной. Поэтому для оценки параметров функции CES применяется более сложный нелинейный метод наименьших квадратов. При спецификации производственной функции, т.е. при решении вопроса о ее принадлежности к тому или иному классу известных функций, может быть полезным знание тех или иных числовых характеристик этих классов функций (отношение средних и предельных показателей, предельная норма замещения, эластичность и др.). Например, при моделировании двухфакторного производства (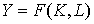) на основе имеющейся статистики 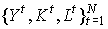можно составить дискретный (разностный) аналог показателя эластичности по капиталу

Если эта величина приблизительно равна постоянному числу для всех t и , для которых разность 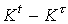достаточно мала, то искомая функция может принадлежать классу функций Кобба-Дугласа. Точно так же, дискретный аналог эластичности замещения может внести ясность относительно принадлежности искомой функции к классу функций CES.

12. Математические модели задачи фирмы.

Для моделирования задач фирмы нам нужно формализовать, такие понятия, как затраты, выпуск, их цены, доход, издержки и производственные возможности фирмы.

Не умаляя общности, будем считать, что фирма производит один вид продукта, используя m видов ресурсов. Эти величины, как и ранее, будем обозначать соответственно через y и 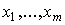. Предположим, что "технология" производства достаточно хорошо изучена, т.е. известна производственная функция .

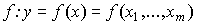Обозначим через p цену выпускаемой продукции, а через 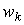- цену k -го вида ресурса, 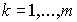. Эти цены порождают понятия дохода (выручки от продажи произведенной продукции) и издержек. Доход от реализации готовой продукции 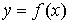определяется формулой 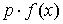. Издержки, соответствующие вектору затрат 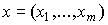, т.е. общие выплаты за все виды затрат, равны 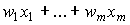. Эти издержки называются переменными издержками, так как они связаны (меняются вместе) с объемом выпуска. Кроме того, фирма несет и постоянные издержки (обозначим ), связанные с расходами на содержание фирмы. Поэтому общие издержки (обозначим C) складываются из двух компонент:

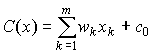
Поскольку постоянные издержки не связаны с выпуском, то при составлении краткосрочных моделей мы их учитывать не будем. Тогда общий результат производства (x,y) (затраты-выпуск) можно оценить величиной

Если эта величина положительна, то пара (x,y) приносит прибыль, в противном случае - убыток.

С помощью полученных формул построим математические модели различных задач фирмы.

1. Долгосрочная задача. На долгосрочный период фирма может планировать любые затраты, поэтому модель задачи имеет вид:

Это есть задача безусловной максимизации прибыли. Здесь постоянные затраты не учтены, так как они не влияют на максимизацию функции P по переменным затратам 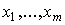. В векторной форме долгосрочная задача имеет вид:

где 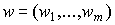- вектор цен затрат.

1. Краткосрочная задача. Эта задача планируется с учетом наличных на данный период запасов ресурсов, поэтому ее модель строится на условную оптимизацию:

где - множество допустимых значений затрат k -го вида. Введя обозначение множества допустимых наборов затрат, эту задачу можно написать в векторной форме

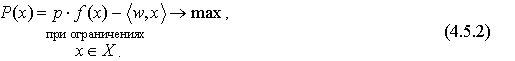
Здесь явный вид множества X может быть описан различными способами. Например, в виде

и т.д.

1. Задача многопродуктового производства. Предположим теперь, что фирма выпускает не один, а несколько (n) видов продуктов. Пусть для каждого j -го вида продукта известны производственная функция и цена 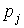(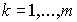); для каждого k -го вида ресурса известны функция , описывающая суммарные затраты этого ресурса для производства всех n видов продуктов, и его наличное количество 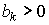(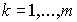). В этом случае модели долгосрочной и краткосрочной задач соответственно имеют вид:

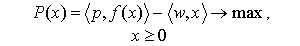
и

Здесь 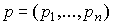- вектор цен выпускаемых товаров, - вектор-функция затрат, - вектор наличных запасов ресурсов.

1. Задача на минимизацию затрат. Во всех приведенных выше моделях производства ставится задача максимизации прибыли, т.е. целевая функция имеет смысл прибыли. Для постановки задачи на минимизацию затрат предположим, что фирма планирует выпуск продуктов в объемах , т.е. рассмотрим фиксированные объемы выпуска. В этом случае оптимизационная задача производства может быть поставлена следующим образом:

Желая "перевыполнить" план выпуска, ограничения-равенства можно заменить на ограничения-неравенства .

1. Видоизменения постановок задач. В зависимости от целей и характера исследования производства, можно пользоваться различными модификациями приведенных выше моделей. Например, по тем или иным техническим соображениям производственную функцию можно "исключить" из целевой функции, записывая их в виде

и

Задачу производства можно поставить в "чисто финансовой" форме. Предположим, что для приобретения необходимых ресурсов выделена фиксированная сумма v. Тогда задачу максимизации дохода можно поставить в следующей форме:

Любое видоизменение моделей допустимо, если оно адекватно описывает реальную задачу. Оценивается не вид модели, а практическая польза от ее применения.

Видно, что во всех моделях производства максимизация и минимизация целевой функции осуществляется по переменным 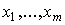, т.е. фирма принимает решение только относительно объемов затрат. Поэтому решениями этих задач являются оптимальные значения векторов затрат. Выбор метода нахождения оптимального решения задач зависит прежде всего от линейности или нелинейности участвующих в их постановке функций f и g. Если эти функции нелинейны, то соответствующую задачу можно решить методом множителей Лагранжа или каким-либо приближенным методом. В случае линейности всех функций можно применить симплекс-метод.

Для примера рассмотрим задачу. Если в ней функции дифференцируемы в и среди них имеются нелинейные, то ее оптимальное решение можно найти с помощью функции Лагранжа

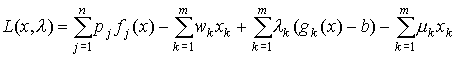
и необходимых условий оптимальности Куна-Таккера.

Предположим, что все функции линейные:

В этом случае целевая функция задачи принимает вид:

Следовательно, мы имеем задачу линейного программирования

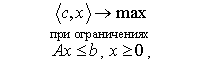
где , A - технологическая матрица, элементы которой показывают расход ресурса вида i для производства единицы продукта вида k. Двойственная к ней задача (правила составления двойственной задачи).

имеет смысл минимизации затрат при фиксированном объеме выпуска.

13. Решение задачи фирмы. Геометрическая иллюстрация.

Пусть производственная функция f дважды дифференцируема в и удовлетворяет условиям . Для нахождения ее оптимального решения (относительно затрат) построим функцию Лагранжа

где , и выпишем необходимые условия Куна-Таккера (см. (2.3.9)-(2.3.11)):

Ввиду предположения о выполнении (4.2.3) эти условия становятся и достаточными условиями оптимальности. Упростим их, предположив . Содержательно это означает необходимость затрат всех видов. Это условие не является жестким, так как в случае можно было исключить ресурс k -го вида из рассмотрения, сократив тем самым размерность пространства затрат.

С учетом последнего предположения из условия дополняющей нежесткости следует . Заметим сразу, что это не противоречит условию о невозможности одновременного равенства нулю всех множителей Лагранжа - оно является следствием изменения условия задачи. В результате необходимый и достаточный признак оптимальности принимает вид:

Величину естественно назвать стоимостью предельного продукта. Поэтому (4.6.1) содержательно означает равенство стоимости предельного продукта и платы за ресурсы в точке :

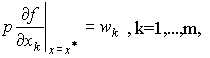
Обозначим

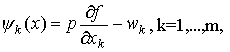
и составим матрицу Якоби для системы (4.6.1):

Из алгебры известно, что если матрица Якоби невырожденна, то система (4.6.1) имеет решение. Здесь невырожденность следует из условий (4.2.2)-(4.2.3). Таким образом, система (4.6.1) разрешима и оптимальное решение задачи (4.5.1) может быть выражено как функция m+1 параметров: :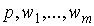

В координатной форме имеем m функций спроса на затраты

выражающих оптимальные объемы затрат в зависимости от цен.

Оказывается, спрос не зависит от масштаба цен, точнее, от пропорционального изменения цены продукции и цен ресурсов. Действительно, из (4.5.1) для любых 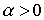имеем:

Так как постоянный коэффициент 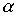не влияет на максимизацию функции P по x, то задача

имеет такое же оптимальное решение, что и задача (4.5.1). Следовательно,

и функции спроса на затраты являются однородными нулевой степени функциями.

Подставляя решение (4.6.2) в производственную функцию f, получаем выпуск как функцию от тех же m+1 параметров:

Это есть функция предложения готовой продукции. Так как

то функция предложения также является однородной нулевой степени функцией, т.е. объем предложения товара остается неизменным при повышении (снижении) цен на ресурсы, если в той же пропорции повышается (снижается) цена готовой продукции.

Рассмотрим теперь геометрическую иллюстрацию оптимального решения (4.6.2) задачи (4.5.1) в пространстве затрат. Для этого введем два геометрических понятия - изокванты и изокосты.

Изокванты в теории производства играют такую же роль, что и кривые безразличия в теории потребления (см. §3.2 и определение 3.2).

Определение 4.2. Изоквантой (производственной функции ) называется геометрическое место всех векторов затрат x, использование которых приводит к одному и тому же объему выпуска продукции .

Таким образом, изокванта - это линия уровня производственной функции. Для различных уровней выпуска y⁰ линии уровня заполняют все пространство затрат () и составляют карту изоквант. Для примера на рис.4.3 приведен вид изоквант

производственной функции Кобба-Дугласа.

Пусть производственная функция 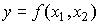дифференцируема по обеим переменным. Тогда вдоль изокванты имеем:

Отсюда найдем отношение:

Следовательно, наклон изокванты производственной функции выражается через отношение предельных продуктов. Дальнейшие геометрические построения, связанные с изоквантами, проведем на рис.4.4. Имея карту изоквант 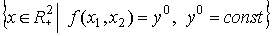, проведем касательные к каждой из них с наклоном . Эти касательные проходят параллельно к оси . Так как изокванты заполняют все пространство , то, соединяя точки касания, получим непрерывную линию Г-1, которую назовем границей первого ресурса.

Аналогично проведем касательные к изоквантам с наклоном 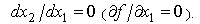. Эти касательные проходят параллельно к оси . Соединяя точки касания, получаем непрерывную линию Г-2, которую назовем границей второго ресурса.

Построенная область в , заключенная между линиями Г-1 и Г-2, называется особой областью. Она характеризуется наотрицательностью обоих предельных продуктов , так как для неположителен. Можно показать, что в особой области справедливы и неравенства (4.2.3), т.е. это та область затрат, где выполнен закон убывающей доходности. Пользуясь условиями (4.2.3), можно доказать, что особая область является выпуклым подмножеством пространства затрат.

Граница первого ресурса Г-1 является геометрическим местом минимального количества затрат 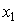, необходимых для производства различных уровней выпуска. Например, для производства продукции в размере необходимо затратить первый ресурс как минимум в 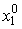единиц (рис. 4.4). Точно также, граница второго ресурса Г-2 является геометрическим местом минимального количества затрат , необходимых для производства различных уровней выпуска. Например, чтобы произвести продукцию в количестве , необходимо как минимум 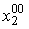единиц второго ресурса.

Изокосты являются своего рода бюджетной линией (см. §3.4).

Определение 4.3. Изокостой называется геометрическое место векторов затрат, для которых издержки производства постоянны:

Для двухфакторного производства изокоста задается уравнением

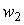Так как цены и предполагаются заданными, дифференцируя последнее уравнение, имеем:

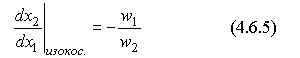
Следовательно, для разных const изокосты являются параллельными линиями с одним и тем же наклоном (рис. 4.5) и этот наклон выражается через отношение цен на ресурсы.

Сравнивая (4.6.4) и (4.6.5), видим:

Покажем, что равенство (4.6.6) достигается именно в точке , являющейся решением задачи (4.5.1). Из (4.6.1) в случае двухфакторного производства имеем:

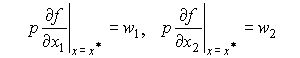
Разделяя первое равенство на второе почленно, получаем

Сопоставляя полученное равенство с (4.6.4) и (4.6.5), приходим к выводу: совпадение наклонов изокванты и изокосты имеет место в одной и той же точке , являющейся оптимальным решением задачи (4.5.1), и эта точка, конечно, является точкой касания изокосты и изокванты (рис.4.6).

Так как изокванты и изокосты заполняют все пространство затрат, соединяя все точки их касания, получаем непрерывную линию. Как легко понять, эта линия расположена в особой области, изображенной на рисунке 4.4, и потому чем дальше на ней расположена точка , тем больше соответствующие значения затрат и выпуска. Поэтому данная линия называется долгосрочным путем расширения производства. Таким образом, геометрическое место пересечений изоквант и изокост показывает оптимальный сценарий развития производства. Этот путь описывает, с одной стороны, затраты, максимизирующие прибыль фирмы, при любом фиксированном уровне издержек, с другой - затраты, минимизирующие издержки, при заданном уровне выпуска (читателю предлагается самостоятельно обосновать эти положения, пользуясь рисунком 4.6). Поэтому долгосрочный путь расширения иногда называют кривой издержек, имея в виду, что вдоль нее оптимальные издержки выражаются как функция от выпуска.

В случае краткосрочной задачи (4.5.2) (или (4.5.3)) необходимый и достаточный признак оптимальности будет иметь более сложный, чем (4.6.1), вид из-за наличия ограничений. Однако и в этом случае при выполнении условий (4.2.2)-(4.2.3) краткосрочный путь расширения, как геометрическое место векторов оптимальных затрат, будет проходить в особой области. Причем можно высказать гипотезу о том, что если множество допустимых затрат X (см. задачу (4.5.2)) краткосрочной задачи имеет непустое пересечение с долгосрочным путем расширения, то краткосрочный путь расширения совпадает (в области X) с долгосрочным путем, т.е. он является частью долгосрочного пути расширения (в случае см. рис. 4.7). Предлагаем читателю доказать эту гипотезу для конкретных видов множества X из задачи (4.5.2), используя примененную выше для задачи (4.5.1) методику.

Если эта гипотеза верна, то для каждой точки на краткосрочном пути существует такое постоянное число 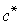, что изокоста и изокванта из долгосрочной задачи будут иметь точкой касания точку . Последнее означает совпадение краткосрочной и долгосрочной кривых издержек, что говорит о согласованности краткосрочной задачи фирмы с ее долгосрочными планами.

14. Анализ влияния цен на объемы затрат и выпуска. Основное уравнение фирмы.

Применяя методику, использовавшуюся в §3.6 для анализа влияния цен на спрос потребителя, можно исследовать чувствительность оптимальных затрат и выпуска к изменениям параметров 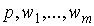. Для этого сделаем дополнительное к условиям предыдущего параграфа предположение: функции и 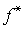дифференцируемы по всем переменным.

Подставляя в систему (4.6.1) функции спроса (4.6.2) и присоединяя к ней выражение для функции предложения (4.6.3), получим замкнутую тождественную систему из m+1 уравнения с m+1 параметром:

Так как чувствительность оптимальных затрат и выпуска по ценам оценивается величинами

то систему (4.7.1) будем дифференцировать по переменным 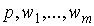. Первые 2m частных производных характеризуют изменение оптимального объема затрат при изменении цены готовой продукции и цен ресурсов; вторая группа частных производных показывает реакцию объема оптимального выпуска на колебание тех же цен.

Ниже мы будем пользоваться следующими обозначениями:

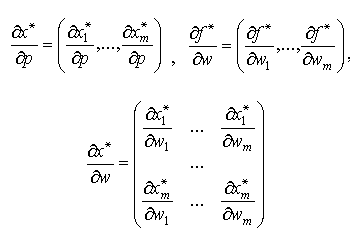
Как и раньше, будем считать выполненными условия (4.2.2)-(4.2.3), т.е. анализ чувствительности затрат и выпуска проведем в пределах особой области, изображенной на рисунке 4.4.

Сначала продифференцируем обе части системы (4.7.1) по p:

Применяя обозначение матрицы Гессе (см. §2.2)

перепишем эту систему в векторной форме:

Продифференцируем теперь систему (4.7.1) по :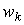

где 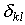- использованный ранее в §3.6 символ Кронекера.

Применяя обозначение единичной матрицы

перепишем эту систему в векторной форме:

Дата добавления: 2015-04-24