
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Моделирование экономики 3 страница
|
|
|
|
Перейдем к вычислению требуемых предельных величин.
- Вычисление предельных величин
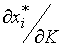 и
и 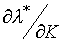 (влияние дохода на
(влияние дохода на 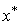 и
и 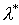 ).
).
Подставим (3.6.1) в систему (3.6.2):
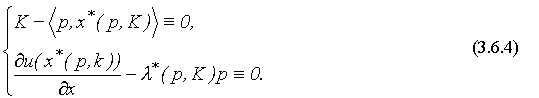
и продифференцируем ее по 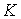 :
:

Перепишем эту систему в форме, удобной для перехода к матричной записи:
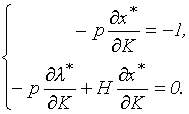
В матричной форме эта система имеет вид:
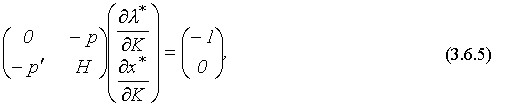
где
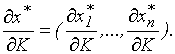
Решая систему (3.6.5), можно найти искомые предельные величины по доходу.
- Вычисление предельных величин
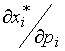 ,
, 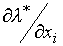 (влияние цены
(влияние цены 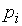 на
на 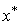 и
и 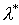 при условии постоянства остальных цен
при условии постоянства остальных цен 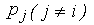 и дохода
и дохода 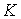 ).
).
Дифференцируя систему (3.6.4) по 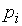 , получаем (в координатной форме):
, получаем (в координатной форме):
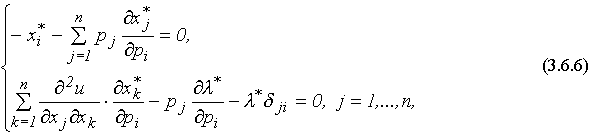
где
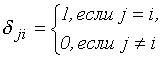
- символ Кронекера. Запишем систему (3.6.6) сначала в векторной, затем в матричной форме:

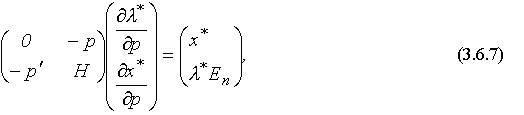
где
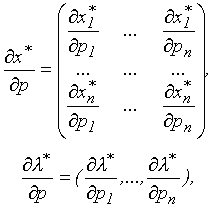
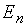 - единичная
- единичная 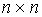 -матрица (
-матрица (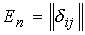 - матрица с нулевыми элементами за исключением диагональных, равных 1).
- матрица с нулевыми элементами за исключением диагональных, равных 1).
Решая систему (3.6.7), можно найти искомые предельные величины по цене i -го товара.
- Вычисление предельных величин
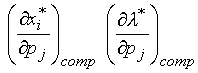 (влияние цен
(влияние цен 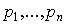 на
на 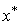 и
и 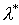 при условии компенсации дохода так, чтобы полезность была неизменной).
при условии компенсации дохода так, чтобы полезность была неизменной).
Используя систему (3.6.2), найдем полные дифференциалы функций u и 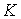 :
:
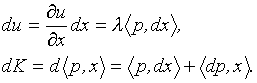
Для того, чтобы полезность оставалась неизменной, т.е. чтобы 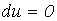 , необходимо, чтобы
, необходимо, чтобы 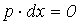 (так как
(так как 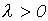 ), а это справедливо, если
), а это справедливо, если 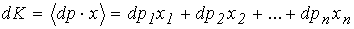 . Содержательно это означает, что при возрастании, например, цены
. Содержательно это означает, что при возрастании, например, цены 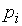 до
до 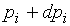 приращение дохода, обеспечивающее неизменность полезности, равно
приращение дохода, обеспечивающее неизменность полезности, равно 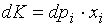 .
.
Дифференцируя (3.6.4) по 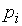 , когда
, когда 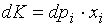 , получаем:
, получаем:
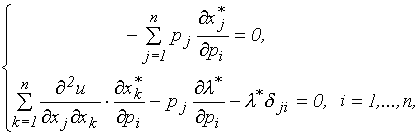
Поясним, что первое уравнение этой системы получается из (3.6.6) при условии
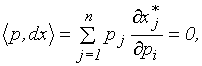
так как в этом случае из (3.6.6) следует 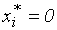 .
.
В векторной форме эта система имеет вид:
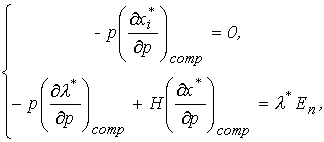
где 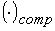 - означает компенсированное изменение цен.
- означает компенсированное изменение цен.
Запишем теперь в матричную форму:
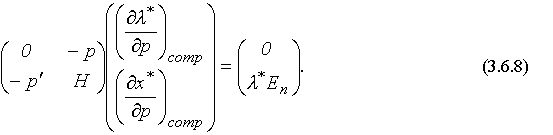
Решая систему (3.6.8), можно найти искомые предельные величины при компенсированном изменении цен.
Все три матричных (3.6.5), (3.6.7) и (3.6.8) могут быть объединены в одно матричное уравнение:
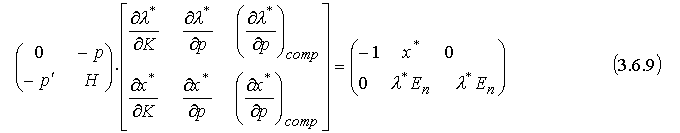
Это уравнение называется основным матричным уравнением теории потребления. Матрица
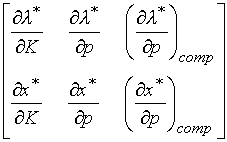
называется матрицей сравнительной статики, а ее элементы - показателями сравнительной статики. Такое название объясняется тем, что эти показатели характеризуют чувствительность 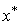 и
и 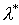 к изменениям параметров
к изменениям параметров 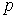 и
и 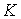 путем сравнения положения оптимума в статике до и после того, как эти параметры изменились.
путем сравнения положения оптимума в статике до и после того, как эти параметры изменились.
7. Уравнение Слуцкого.
Основное матричное уравнениеможно записать следующим образом:
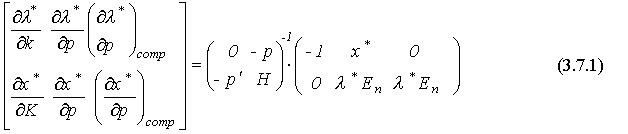
Решение этой системы относительно показателей сравнительной статики по спросу имеет вид:
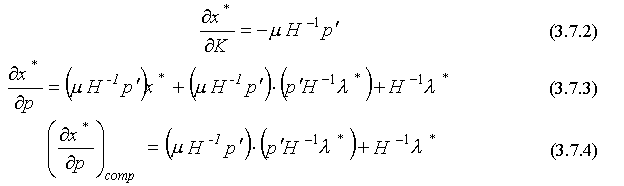
Здесь 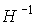 - обратная матрица Гессе, а
- обратная матрица Гессе, а
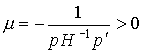
- скалярная величина. Можно показать, что
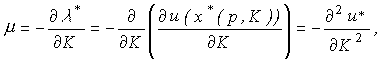
поэтому скаляр 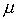 можно интерпретировать как коэффициент убывания предельной полезности денег.
можно интерпретировать как коэффициент убывания предельной полезности денег.
Сравнивая (3.7.3) и (3.7.4) замечаем, что
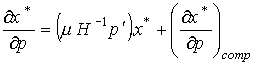
Сопоставляя это уравнение с (3.7.2), получаем,
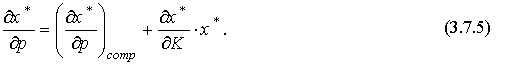
Равенство (3.7.5) называется уравнением Слуцкого. Это же уравнение называют основным уравнением теории ценности.
В координатной форме уравнение Слуцкого выглядит так:
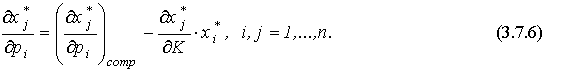
Левую часть уравнения принято называть общим эффектом (от влияния цены на спрос), первое слагаемое в правой части - влиянием замены (т.е. компенсированного изменения цены на спрос), второе слагаемое - влиянием дохода (влияние изменения дохода на спрос). Перепишем уравнение следующим образом:
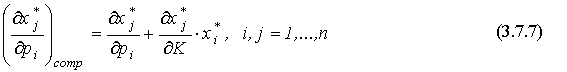
Из (3.7.4) следует, что матрица влияния замены симметрична и отрицательно определена (установите это самостоятельно). Из отрицательной определенности следует

Отсюда вывод - компенсированное возрастание цены товара приводит к уменьшению спроса на этот товар.
Их симметричности матрицы влияния замены и уравнения (3.7.7) получаем:
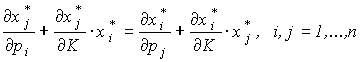
Поэтому уравнение Слуцкого, в частности, означает, что:
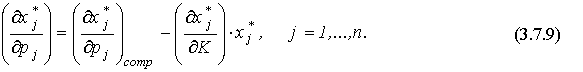
Здесь производная 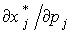 называется влиянием на спрос (на j -й товар) изменения частной цены (цены j -го товара). Равенство (3.7.9) используют для характеристики типов товаров.
называется влиянием на спрос (на j -й товар) изменения частной цены (цены j -го товара). Равенство (3.7.9) используют для характеристики типов товаров.
Определение 3.4. Товар вида j называется нормальным, если  ; товаром Гиффина, если
; товаром Гиффина, если 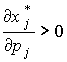 ; ценным, если
; ценным, если 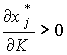 ; малоценным, если
; малоценным, если  . Два товара i и j являются взаимозаменяемыми, если
. Два товара i и j являются взаимозаменяемыми, если 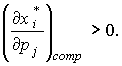 взаимодополняемыми, если
взаимодополняемыми, если 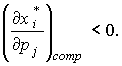
Как следует из (3.7.8) и (3.7.9), должно быть
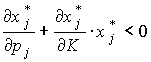
С учетом условия 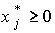 приходим к следующим выводам:
приходим к следующим выводам:
а) если 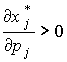 , то обязательно
, то обязательно  ;
;
б) если 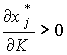 , то обязательно
, то обязательно  .
.
Отсюда, товар Гиффина не может быть ценным, т.е. он обязательно малоценный.
В общем случае каждый товар попадает в одну из следующих категорий.
- Нормальный и ценный (
 ;
; 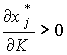 );
); - Нормальный и малоценный (
 ;
;  );
); - Товар Гиффина и малоценный (
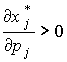 ;
;  ).
).
Существование товара Гиффина кажется не вполне реальным. Действительно, его определение противоречит закону о спросе (спрос есть убывающая функция цены). Однако, когда какой-либо популярный среди населения товар продается по слишком низкой цене, появляется подозрение о его качестве. Это может оказаться причиной снижения спроса на него. Последующее же поднятие цены может повысить спрос на этот товар.
Нормальный и ценный товар отличается от нормального малоценного товара высоким качеством. Например, фрукты южных сортов по питательным и вкусовым качествам превосходят северные сорта, но они и дороже; масло дороже маргарина, так как качество его выше; вычислительная техника завода-изготовителя, как правило, качественнее и поэтому дороже, чем та же техника, но лицензионной сборки и т.д.).
Умножим обе части равенства (3.7.4) на вектор p:
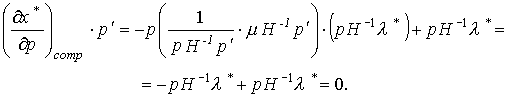
Следовательно, в координатной форме имеем:
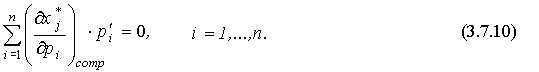
Принимая во внимание положительность всех цен и неравенство (3.7.8), приходим к выводу о том, что для каждого j существует i (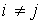 ) такое, что
) такое, что
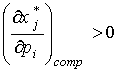
Таким образом, в наборе 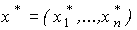 каждому товару соответствует по крайней мере один такой товар, который составляет с ним взаимозаменяемую пару.
каждому товару соответствует по крайней мере один такой товар, который составляет с ним взаимозаменяемую пару.
Из уравнения Слуцкого (3.7.5) и равенства (3.7.10) получаем
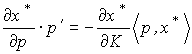
или
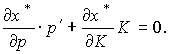
Запишем это равенство в координатной форме
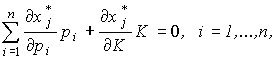
и разделим обе части каждого из n равенств на 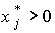 :
:
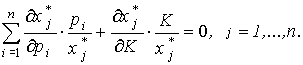
В обозначениях эластичности (см. (3.3.2), (3.5.4)) имеем:
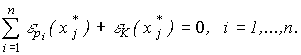
Отсюда вывод: для каждого товара j сумма всех n перекрестных эластичностей спроса по цене и эластичности спроса по доходу должна быть равна нулю, т.е. сумма всех эластичностей по цене равна отрицательной эластичности по доходу.
8. Основные элементы модели производства.
Под производством понимается процесс взаимодействия экономических факторов, завершаемый выпуском какой-либо продукции. Правила, предписывающие определенный порядок взаимодействия экономических факторов, составляют способ производства или, иначе говоря, технологию производства. Производство - основная область деятельности фирмы (или предприятия). Фирма - это организация, производящая затраты экономических ресурсов для изготовления продукции и услуг, которые она продает потребителям, в том числе, другим фирмам. Производственными единицами являются не только заводы и фабрики, но и отдельные лица - фермеры, ремесленники и др.
Производство можно представить как систему "затраты-выпуск", в которой выпуском является то, что фактически произведено, а затратами - то, что потребляется с целью выпуска (капитал, труд, энергия, сырье). Поэтому формально можно сказать, что производство - это функция, которая каждому набору затрат и конкретной технологии ставит в соответствие определенный выпуск. Именно такое упрощенное понимание производства как "черного ящика" заложено в математической модели производства. Во "вход" этого черного ящика подаются затраты, а на "выходе" получаем выпуск (произведенную продукцию).
Подобное описание производства на первый взгляд кажется сильно абстрактным, так как в нем не отражены технологические процессы, происходящие внутри черного ящика. В математической модели технология производства учитывается обычно посредством задания соотношений между затратами и выпуском т.е. нормой затрат каждого из ресурсов, необходимых для получения одной единицы выпускаемой продукции. Такой подход объясняется тем, что математическая экономика изучает суть экономических процессов, а сугубо технические операции как таковые (а не их экономические следствия) остаются за рамками этой науки.
Задача фирмы, как производственной единицы, сложна и многогранна - начиная от организации производства и кончая благотворительной деятельностью. Естественно, математической моделью нельзя охватить весь спектр деятельности фирмы и отразить все преследуемые цели. Поэтому при формализации задачи рационального функционирования фирмы учитываются лишь основные конечные цели.
Конечной целью фирмы является получение наибольшей прибыли от реализации своей продукции. Напомним в этой связи, что прибыль понимается как разность двух величин: выручки от реализации продукции (дохода) и издержек производства. Издержки производства равны общим выплатам за все виды затрат, иначе говоря, издержки - это денежный эквивалент материальных затрат. В общем случае издержки состоят из двух слагаемых: постоянных издержек и переменных издержек. Постоянные издержки (расходы на закупку и ремонт оборудования, содержание фирмы, страховку и пр.) фирма несет независимо от объема выпуска. Переменные издержки (расходы на заработную плату, сырье и пр.) касаются использования уже имеющихся в распоряжении фирмы ресурсов, производственных мощностей и меняются вместе с объемом выпуска.
Согласно с поставленной целью, задача фирмы сводится к поиску такого способа производства (сочетания затрат и выпуска), который обеспечивает ей наибольшую прибыль с учетом и в рамках имеющихся у нее ограниченных ресурсов. Данная трактовка цели фирмы и наилучшего способа производства не является единственно возможной. Речь идет о некоторой гипотезе относительно предпочтений производителя, а не о логической необходимости. В действительности же мотивы принимаемых руководителями фирм решений могут быть продиктованы другими соображениями, например, гуманного или социально-политического характера. Поэтому в отличие от математической теории потребления, где существовала единственная, логически оправданная оптимизационная модель потребителя, здесь нецелесообразно говорить об "оптимизационной модели фирмы" как таковой. Задачи фирмы могут существенно отличаться как преследуемой целью, так и временным периодом ее решения.
Обсужденную выше задачу будем называть задачей фирмы на максимизацию прибыли. Двойственной к ней (в некотором смысле) является задача фирмы на минимизацию издержек при фиксированном уровне планируемого выпуска (дохода). Именно такая формализация цели производства в последнее время становится более популярной в связи с глобальной проблемой "устойчивого развития" общества, так как она созвучна с задачами рационального использования природных ресурсов.
Из приведенного выше краткого описания сути производства видно, что основными факторами, которые должны быть учтены при моделировании задачи фирмы, являются выпуск продукции, затраты ресурсов, их цены, доход, издержки и производственные возможности фирмы. Перед тем, как построить ту или иную оптимизационную модель задачи фирмы, более подробно остановимся на способах формализации этих понятий и рассмотрим некоторые их свойства.
9. Пространство затрат и производственная функция.
Предположим, что фирма производит n видов продуктов. Виды продуктов будем обозначать индексом j, а их количества - через 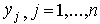 . Технология производства каждого вида продукта требует использования ряда ресурсов в некоторых количествах. Двойными индексами
. Технология производства каждого вида продукта требует использования ряда ресурсов в некоторых количествах. Двойными индексами 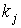 обозначим виды ресурсов, используемых для выпуска продукта вида j. Пусть
обозначим виды ресурсов, используемых для выпуска продукта вида j. Пусть 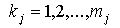 .. Обозначим через
.. Обозначим через 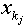 - количества этих ресурсов,
- количества этих ресурсов, 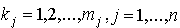 . Следовательно, имеется всего
. Следовательно, имеется всего  видов ресурсов.
видов ресурсов.
Использование такой двойной индексации привлекательно с точки зрения информативности (видно, какой ресурс относится к какому продукту), но неудобно чисто технически. Во-первых, усложняется запись формул; во-вторых, увеличивается размерность задачи (т.к. среди 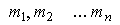 могут быть одни и те же наименования) и, в-третьих, такие операции как сложение, вычитание затрат в векторной форме, а также составление уравнений становятся невозможными без дополнительных преобразований индексов (идентификация, упорядочение и т.д.).
могут быть одни и те же наименования) и, в-третьих, такие операции как сложение, вычитание затрат в векторной форме, а также составление уравнений становятся невозможными без дополнительных преобразований индексов (идентификация, упорядочение и т.д.).
Поэтому в дальнейшем виды ресурсов будем обозначать одинарными индексами k, их количества - 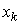 , где
, где 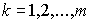 . Здесь m - достаточно большое число (равное сумме
. Здесь m - достаточно большое число (равное сумме  , где каждый ресурс считается только один раз). Теперь можно говорить, что для производства n видов продуктов фирма использует m видов затрат. Это не приводит к недоразумениям, так как в случае неиспользования k -го ресурса для выпуска данного продукта полагаем
, где каждый ресурс считается только один раз). Теперь можно говорить, что для производства n видов продуктов фирма использует m видов затрат. Это не приводит к недоразумениям, так как в случае неиспользования k -го ресурса для выпуска данного продукта полагаем  .
.
Введем в рассмотрение два вида векторов: 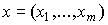 - вектор затрат и
- вектор затрат и 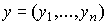 - вектор выпуска. Положительный ортант
- вектор выпуска. Положительный ортант
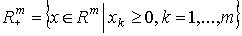
называется пространством затрат. Аналогично определяется пространство выпуска:
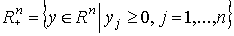
Для отражения реальных возможностей фирмы в математических моделях часто применяются более узкие множества 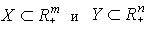 .
.
Технологическая связь между затратами и выпуском описывается с помощью производственной функции.
Определение 4.1. Любая функция 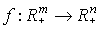 , ставящая в соответствие каждому вектору затрат x вектор
, ставящая в соответствие каждому вектору затрат x вектор 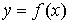 максимального выпуска, который может быть получен при этих затратах, называется производственной функцией.
максимального выпуска, который может быть получен при этих затратах, называется производственной функцией.
Это есть определение производственной функции для многопродуктовой фирмы, т.е. векторной производственной функции. Если фирма выпускает только один вид продукта, то производственная функция является скалярной: 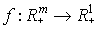 или
или

В общем случае производственную функцию можно записать в неявной форме: 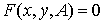 , где A -
, где A - 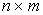 -матрица параметров (технологическая матрица). В некоторых моделях применяется следующее выражение для производственной функции:
-матрица параметров (технологическая матрица). В некоторых моделях применяется следующее выражение для производственной функции: 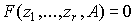 , где переменные
, где переменные 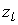 со знаком "-" обозначают затраты, а со знаком "+" - выпуски.
со знаком "-" обозначают затраты, а со знаком "+" - выпуски.
Если в качестве независимых переменных (аргументов) выступают затраты (см. (4.2.1)), то производственную функцию иногда называют функцией выпуска, если же фиксирована величина выпуска (y), то производственная функция является функцией затрат ( ). Таким образом, функция выпуска и функция затрат являются взаимно обратными друг другу функциями.
). Таким образом, функция выпуска и функция затрат являются взаимно обратными друг другу функциями.
Применение производственных функций не ограничивается выявлением зависимости затраты-выпуск. Различные приемы математического аппарата позволяют использовать их для вычисления численных характеристик производства, анализа эффективности изменения масштаба производства и технологического прогресса, исследования эластичности производственных факторов, рационального ведения хозяйства, оптимального планирования и прогнозирования вариантов развития фирмы и др.
Поэтому очень важно, чтобы производственная функция объективно отражала моделируемую действительность, т.е. чтобы она удовлетворяла содержательно-логическим и экономическим требованиям. Основные из них следующие:
- в число аргументов производственной функции должны быть включены все существенные для данного процесса факторы;
- все величины должны иметь отчетливый экономический смысл;
- все экономические величины, входящие в производственную функцию, должны быть измеримы;
- выпуск продукции без затрат невозможен;
- если величина какого-либо ресурса ограничена, то выпуск не может расти бесконечно;
- увеличение затрат не может привести к уменьшению выпуска.
Вопрос об адекватном описании экономической реальности на языке производственных функций тесно связан с их математическими свойствами. Ради простоты эти свойства приведем для однопродуктового производства, т.е. для производственной функции вида (4.2.1).
- Монотонность: из
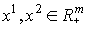 и
и 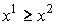 следует
следует 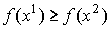 .
. - Вогнутость: для любых
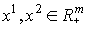 и
и 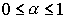 справедливо неравенство
справедливо неравенство 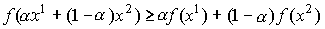 .
. - Поведение в начале координат:
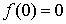 .
. - Однородность:
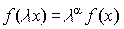 , где
, где 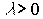 - масштабное число,
- масштабное число, 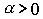 - степень однородности.
- степень однородности.
Если производственная функция дифференцируема по всем аргументам, то свойства 1 и 2 соответственно могут быть заменены следующими неравенствами:

Частные производные 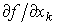 называются предельными продуктами. Условие (4.2.2), как и свойство 1, означает, что увеличение любого вида затрат не приводит к уменьшению выпуска. Условие (4.2.3) показывает, что увеличение затрат одного вида ресурса (при постоянном уровне затрат других ресурсов) приводит ко все меньшему приросту выпуска. Это свойство в экономической теории называется законом убывающей доходности (отдачи).
называются предельными продуктами. Условие (4.2.2), как и свойство 1, означает, что увеличение любого вида затрат не приводит к уменьшению выпуска. Условие (4.2.3) показывает, что увеличение затрат одного вида ресурса (при постоянном уровне затрат других ресурсов) приводит ко все меньшему приросту выпуска. Это свойство в экономической теории называется законом убывающей доходности (отдачи).
Свойство 3 является отражением бездеятельности, так как без затрат нет и выпуска. Свойство 4 описывает реакцию производства на изменение затрат. Параметр 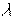 показывает масштаб изменения производства (расширения производства - если
показывает масштаб изменения производства (расширения производства - если 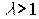 , сужения производства - если
, сужения производства - если 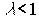 ), а
), а 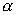 - эффект от изменения масштабов производства. Если
- эффект от изменения масштабов производства. Если 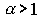 , то одновременное увеличение всех факторов в
, то одновременное увеличение всех факторов в 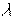 раз приводит к возрастанию объема выпуска больше, чем в
раз приводит к возрастанию объема выпуска больше, чем в 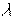 раз (
раз (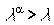 ), т.е. эффект от расширения масштаба производства положителен. При
), т.е. эффект от расширения масштаба производства положителен. При 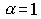 получаем:
получаем: 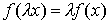 - выпуск возрастает в той же пропорции, что и затраты. Такие функции называются линейно-однородными (или однородными в первой степени).
- выпуск возрастает в той же пропорции, что и затраты. Такие функции называются линейно-однородными (или однородными в первой степени).
Если
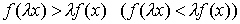
то говорят о возрастающем (убывающем) доходе от расширения масштаба производства. Заметим, что свойство 4 определено в точке, тогда как свойства 1 и 2 - во всем пространстве затрат.
Как мы видим, перечисленные (желательные) свойства производственной функции вполне согласуются с ее определением, так как они касаются только соотношения затраты-выпуск. Действительно, здесь нет никаких требований на бесперебойную работу станков, нормирования движения конвейера и т.д. Поэтому производственная функция, как отображение количественной связи между затратами и выпуском, представляет собой регрессионную модель (см. §2.5). Следовательно, она может быть построена на основе статистических данных и с применением методов математической статистики. Оставляя подробное обсуждение этого вопроса до §4.4, сейчас мы приведем примеры наиболее удачно построенных и потому часто применяемых на практике производственных функций. При этом для простоты будем рассматривать двухфакторную однопродуктовую производственную функцию вида
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 441; Нарушение авторских прав?; Мы поможем в написании вашей работы!