Моделирование экономики 10 страница

Теорема 6.4. Если выполнены условия а)-д), то в модели Неймана (6.4.8) существует состояние равновесия.

Условия в) и г) говорят о наличии в каждом столбце матрицы A и каждой строке матрицы B по крайней мере одного положительного элемента. Содержательно это означает, что среди всех производственных процессов нет таких, которые ничего не тратят, и каждый из n видов продуктов действительно производится. Условие д) имеет чисто техническое предназначение.

Определение 6.5. Число

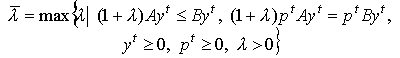
называется максимальным темпом сбалансированного роста, а число

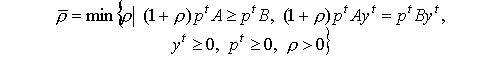
называется минимальной нормой процента.

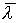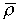Оказывается, что в состоянии равновесия числа и существуют и равны между собой:

если только начальные точки y⁰ и p⁰ также удовлетворяют этому равенству.

Траектория производства 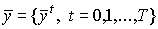, удовлетворяющая условиям (6.4.13) пр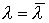и и 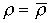и соответствующая максимальному сбалансированному росту, т.е. 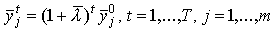, называется траекторией равновесного роста (или траекторией Неймана, или магистралью). Поскольку эту траекторию можно представить в ви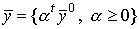де , где 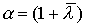, то ее еще называют лучом Неймана а цены (6.4.12), соответствующие минимальной норме процента 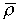, называют неймановскими ценами.

24. Магистральные траектории в линейных моделях экономики.

В математической экономике магистралью называется траектория экономического роста, на которой пропорции производственных показателей (такие как темп роста производства, темп снижения цен) неизменны, а сами показатели (такие как интенсивность производства, валовый выпуск) растут с постоянным максимально возможным темпом. Таким образом, магистраль - это траектория или луч максимального сбалансированного роста. Ее часто сравнивают со скоростной автострадой. Так, например, для того чтобы добраться из Кемерово в Киселевск как можно быстрее, наиболее целесообразно сначала проехать по автостраде Кемерово-Новокузнецк, а затем уже съехать на ответвляющуюся от нее дорогу в районе Киселевска. Так мы потеряем на дорогу меньше времени и доедем до конечного пункта с большим комфортом, чем если бы мы ехали по обычному шоссе через Ленинск-Кузнецкий и Белово.

Поскольку "оптимальное" или "эффективное" развитие экономики в любом смысле так или иначе связано и должно сопровождаться экономическим ростом, то для достижения любой конечной цели следует поступать аналогичным образом: сначала вывести производство на магистральный путь, т.е. на траекторию (или луч) Неймана, характеризующуюся максимальным темпом роста 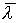и минимальной нормой процента 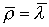(см. (6.4.14)), а по истечении определенного срока времени вывести ее к задуманной цели. Такими целями могут быть максимизация прибыли, минимизация затрат, максимизация полезности от потребления товаров, достижение конкурентного равновесия при наиболее благоприятных условиях, т.е. на более высоком уровне благосостояния населения, и т.д.

Итак, с одной стороны мы имеем магистральные модели, а с другой - оптимизационные или еще шире - нормативные модели экономики. Изучение этих двух моделей во взаимосвязи, т.е. изучение связи между магистральными и оптимальными (в том или ином смысле) траекториями и является предметом магистральной теории. Можно говорить, что магистральная теория является одним из средств качественного анализа оптимальных траекторий. Основной целью этой теории является исследование условий так называемых "слабой" и "сильной" теорем о магистралях. Слабая теорема утверждает, что за исключением некоторого малого периода 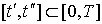(или некоторого числа дискретных моментов из 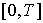), не зависящего от продолжительности T планового периода, все оптимальные траектории сосредотачиваются в относительной близости к магистральной траектории. Сильная теорема говорит о том, что те небольшие промежутки времени 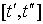, на которых оптимальные траектории удалены от магистральной, если они существуют, то разве лишь в начале периода 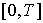, т.е. 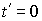, или в конце периода 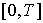, т.е. 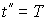; а в середине периода оптимальные траектории расположены в относительной близости к магистральной.

В общем случае в моделях экономической динамики даже при неизменности технологических возможностей утверждения теорем о магистрали не выполняются. Для их выполнения приходится вводить различные дополнительные предположения о свойствах исходной модели экономики. Другой путь состоит в изучении реальных отраслевых пропорций и сравнении их с магистральными. Благодаря техническому прогрессу и изменчивости во времени общественных предпочтений различных благ, реальное состояние экономики при детальном (дезагрегированном) ее описании всегда значительно отличается от магистрального. В то же время, как показывают полученные в этом направлении результаты исследований, при высоком уровне агрегирования экономические пропорции близки к магистральным.

Теоремы о магистралях доказываются для ряда оптимизационных моделей расширяющейся экономики. Наиболее общей из них является известная теорема Раднера для нелинейных моделей расширения (см. §7.2). Здесь мы приведем подобные теоремы для линейных моделей Леонтьева и Неймана. Единственная наша цель - дать читателю начальное представление о магистральной теории. Поэтому приводить сложные доказательства теорем и заниматься подробным и строгим анализом их условий не будем. Для более углубленного изучения магистральной теории можно рекомендовать книги [2, 16].

На основе модели Неймана (6.4.8) могут быть построены различные оптимизационные задачи. Одна из возможных постановок выглядит так:

В этой задаче требуется найти такую траекторию 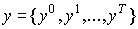, чтобы доход от продажи всего выпуска к концу планового периода был максимальным при условии, что затраты каждого периода не превышают выпусков предыдущего периода.

Всякую траекторию, удовлетворяющую условиям (6.5.2) и доставляющую максимальное значение целевой функции (6.5.1), будем называть оптимальной траекторией и обозначать через 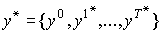(здесь 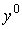- установившаяся к началу планового периода интенсивность выпуска). В общем случае в данной задаче может существовать не одна оптимальная траектория.

Предположим, что в модели Неймана, представленной ограничениями (6.5.2), существует единственная стационарная траектория 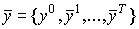производства, соответствующая максимальному темпу сбалансированного роста 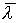, т.е. 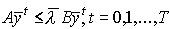. Поскольку 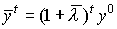, где в любой момент t 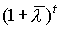есть скаляр, то вместо предыдущего неравенства можно писать 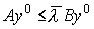. Далее, имея в виду представление 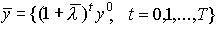, мы условно можем написать .

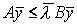В дальнейшем нам понадобится понятие "расстояния" между векторами интенсивностей в пространстве 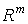. Под расстоянием между двумя векторами интенсивностей 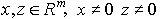, будем понимать число

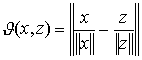
где 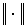- норма вектора, т.е. число, равное длине данного вектора. Объясним наглядно смысл такого расстояния. Для удобства обозначим 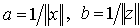. Тогда

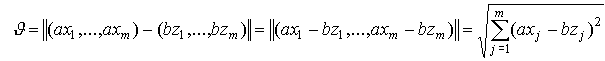
Далее, для любого вектора x длина вектора 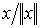равна единице. Действительно, так как норма числа есть само число, то

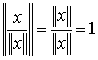
Например, для 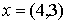имеем:

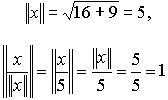
Поэтому 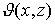равно длине отрезка между точками 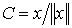, 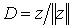(рис. 6.5), лежащими на единичной окружности. Из этого рисунка видно: 1) если возможно представлени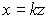е , где 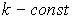(т.е. x и z коллинеарные вектора), то 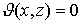; 2) для , .

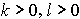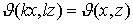Нетрудно видеть, что 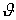есть непрерывная по обоим аргументам функция.

С помощью введенного понятия расстояния дадим строгое определение понятия магистрали в задаче (6.5.1)-(6.5.2).

Определение 6.6. Луч Неймана 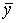называется сильной магистралью в задаче (6.5.1)-(6.5.2), если для каждого 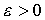существуют такие зависящие от 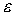(но не зависящие от T) числа 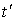и 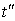, что для всякой оптимальной траектории 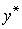этой задачи и для всех .

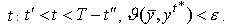Заметим, что ввиду второго свойства расстояния 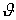для всех .

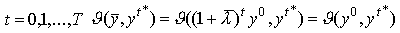Из определения следует, что постоянный луч 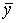как бы аппроксимирует оптимальные траектории: всякая оптимальная траектория 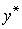почти все время идет вдоль луча 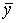, т.е. она сохраняет высокий (почти максимальный) темп интенсивностей производственных процессов, если только величина T горизонта планирования много больше, чем 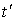и .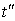

Приведем для полноты и понятие слабой магистрали.

Определение 6.7. Луч Неймана 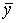называется слабой магистралью в задаче (6.5.1)-(6.5.2), если для любого 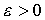существует такое (зависящее от 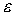) число r, что для любой оптимальной траектории 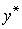этой задачи неравенство 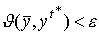нарушается не более чем для r моментов t, 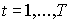, причем число r не зависит от длины T планового периода.

Очевидно, сильная магистраль является одновременно и слабой магистралью (достаточно положить ).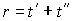

Прежде чем сформулировать теорему о магистрали для задачи (6.5.1)-(6.5.2), рассмотрим более простой и частный случай этой модели - динамический аналог оптимизационной задачи Леонтьева (6.2.14)-(6.2.15):

где A - 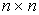-технологическая матрица, 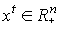- вектор валового выпуска в момент t, 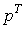- вектор цен в момент T.

В модели Леонтьева (6.2.1) равенство 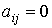означает, что отрасль i не нуждается в товарах отрасли j. Вообще говоря, может существовать целая группа отраслей 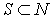( 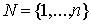- множество всех отраслей), которые не нуждаются в товарах отраслей из множества 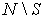, а для своего производства обходятся только товарами из группы S. В этом случае говорят, что множество отраслей S изолировано от остальных в том смысле, что эта группа отраслей может функционировать отдельно от остальных.

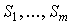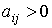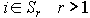Матрица A называется неразложимой, если во множестве всех отраслей N нет изолированных подмножеств. Неразложимость матрицы A означает, что каждая отрасль использует продукцию всех отраслей. Неразложимая матрица A называется примитивной, если множество N нельзя разбить на непересекающиеся подмножества , такие, что если для , то 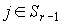, а при 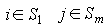. Читателю предлагается самому истолковать содержательный смысл примитивности технологической матрицы A.

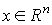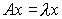Приведем еще несколько необходимых определений. Собственным вектором матрицы A называется такой ненулевой вектор , что , где 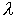- некоторый скаляр, называемый собственным числом матрицы A, соответствующим собственному вектору x. Неотрицательный собственный вектор неотрицательной неразложимой матрицы A называется вектором Фробениуса матрицы A, а соответствующее ему собственное число - числом Фробениуса матрицы A.

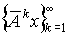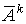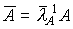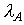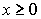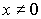Неразложимая матрица A называется устойчивой, если для любого x последовательность сходится, где - k -ая степень матрицы , - число Фробениуса для матрицы A. Предельной точкой этой последовательности при и является вектор 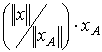, где 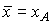- вектор Фробениуса для матрицы A.

Примитивная матрица всегда устойчива.

Относительно задачи (6.5.3)-(6.5.4) сделаем следующие предположения:

1. ;
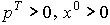2. матрица A неотрицательна, неразложима и примитивна.

Теорема 6.5. Если выполнены условия 1), 2), то сильной магистралью в задаче (6.5.3)-(6.5.4) является вектор Фробениуса 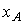матрицы A, т.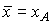е. , где 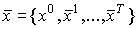- стационарная траектория динамической модели Леонтьева (6.5.4) ().

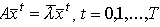Целевая функция в задаче (6.5.3)-(6.5.4) относится к конечному моменту планового периода и называется терминальной. В динамической оптимизационной задаче Леонтьева с нетерминальной целевой функцией возникает так называемая проблема горизонта планирования. Дело в том, что по оптимальной траектории выпуск к моменту T может оказаться недостаточным для обеспечения нормального функционирования экономики за горизонтом планирования. Поэтому требуется наложить специальные ограничения снизу на вектор 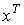, что приводит к дополнительным сложностям при исследовании магистральных свойств оптимальных траекторий.

Вернемся теперь к задаче Неймана (6.5.1)-(6.5.2) и предположим выполненными следующие условия:

а) существует такое число 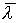, что соотношения 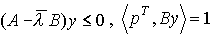определяют единственный вектор ;
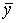в) ;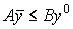
г) существует стационарная траектория цен ;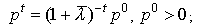
д) матрица A неотрицательна, неразложима и примитивна;
е) для любого достаточно малого числа 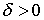существуют такие (зависящие от 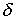) числа 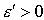и 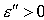, что для оптимальной траектории 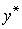из неравенства 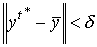вытекают неравенства .

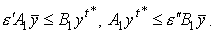В последнем условии A₁ и B₁ - это такие подматрицы матриц A и B (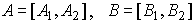), что .

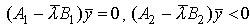В отличие от условий а)-д), допускающих соответствующие экономические интерпретации, условие е) носит чисто технический характер и нужно сугубо для доказательства следующей теоремы.

Теорема 6.6. При выполнении условий а)-е) для любого 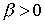существует такое число 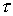, не зависящее от T, что для любой оптимальной траектории 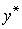задачи (6.5.1)-(6.5.2) выполняется условие 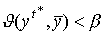для всех .

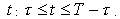Эта теорема утверждает, что почти все время все оптимальные траектории 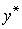близки к сильной магистрали .

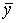Важная роль магистральных траекторий состоит также в том, что в случае отсутствия возможности вычисления оптимальных траекторий при планировании производства можно ориентироваться на движение по лучу Неймана, т.е. планировать функционирование отраслей с интенсивностями, близкими к тем, которые задаются стационарной траекторией .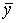

Дата добавления: 2015-04-24